Draw a graph between terminal velocity of a spherical body and square of its radius?
To draw a graph between the terminal velocity (VT) of a spherical body and the square of its radius (R^2), we can follow these steps:
1. Understand the Relationship:
The terminal velocity (VT) of a spherical body falling through a fluid is given by the equation:
VT=29⋅(R2)(ρ−σ)gη
where:
- R = radius of the spherical body,
- ρ = density of the spherical body,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = viscosity of the fluid.
2. Identify the Proportionality:
From the equation, we can see that terminal velocity VT is directly proportional to the square of the radius R2. This can be expressed as:
VT∝R2
3. Rearranging the Equation:
To plot the graph, we can express this relationship in a more useful form:
VTR2=29⋅(ρ−σ)gη
This indicates that if we plot VT on the y-axis and R2 on the x-axis, the graph will be a straight line passing through the origin.
4. Plotting the Graph:
- On the x-axis, label it as R2 (the square of the radius).
- On the y-axis, label it as VT (terminal velocity).
- Since VT is directly proportional to R2, draw a straight line starting from the origin (0,0) and extending upwards to the right.
5. Determine the Slope:
The slope of the line can be determined from the rearranged equation:
slope=29⋅(ρ−σ)gη
This slope represents how much the terminal velocity increases with the increase in the square of the radius.
Final Graph:
The final graph will be a straight line that starts from the origin, indicating that as the square of the radius increases, the terminal velocity also increases proportionally.
---
The terminal velocity (VT) of a spherical body falling through a fluid is given by the equation:
VT=29⋅(R2)(ρ−σ)gη
where:
- R = radius of the spherical body,
- ρ = density of the spherical body,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = viscosity of the fluid.
From the equation, we can see that terminal velocity VT is directly proportional to the square of the radius R2. This can be expressed as:
VT∝R2
To plot the graph, we can express this relationship in a more useful form:
VTR2=29⋅(ρ−σ)gη
This indicates that if we plot VT on the y-axis and R2 on the x-axis, the graph will be a straight line passing through the origin.
- On the x-axis, label it as R2 (the square of the radius).
- On the y-axis, label it as VT (terminal velocity).
- Since VT is directly proportional to R2, draw a straight line starting from the origin (0,0) and extending upwards to the right.
The slope of the line can be determined from the rearranged equation:
slope=29⋅(ρ−σ)gη
This slope represents how much the terminal velocity increases with the increase in the square of the radius.
The final graph will be a straight line that starts from the origin, indicating that as the square of the radius increases, the terminal velocity also increases proportionally.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Short Answer Questions
162 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions
33 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Curiosity Questions
9 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Knowledge Check
The nature of graph between terminal velocity of spherical body vs the square of its radius is
Aexpoentially increasin curveBstaight lineCparabolaDexponentially decreasing curveTerminal velocity (V) of a spherical object varies with a radius of object (r) -
A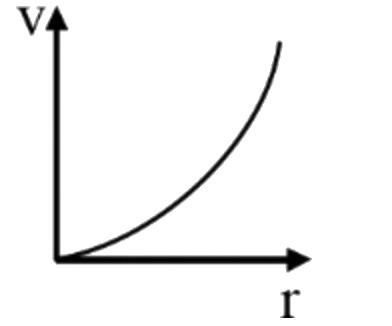 B
B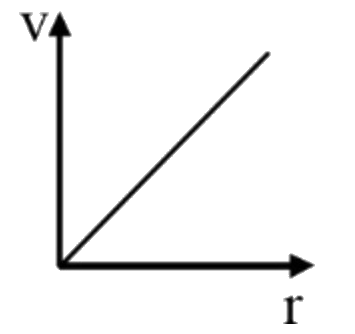 C
C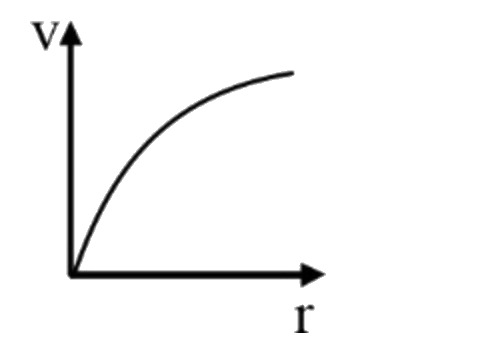 D
D
For a body of given mass graph between velocity of the body and its linear momentum is
Aa straight line with slope =0Ba straight line with positive slopeCa straight line with negative slopeDa parabola
The terminal velocity of a small sized speherical body of radius r falling in a viscous liquid is proportional to :
View SolutionA graph between the square of the velocity of a particle and the distance(s) moved is shown in figure. The acceleration of the particle in kilometers per hour square is:-
View SolutionA graph between the square of the velocity of a particle and the distance(s) moved is shown in figure. The constant acceleration of the particle in kilometer per hour square is:

View SolutionThe terminal velocity of small sized spherical body of radius r falling vertically in a viscous liquid is given by the following proportionality
View SolutionThe terminal velocity V of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
View Solution
