Two soap bubble of radii r1 and r2 combime to form a single bubble of radius r under isothermal conditions . If the external pressure is P, prove that surface tension of soap solution is given by S=P(r3−r31−r32)4(r21+r22−r2).
Excess of pressure in a soap bubble of radius r1 is
P1−P=4Sr1orP1=P+4Sr1
Similarly, pressure inside the bubble of radius r is
P'=P+(4S)(r)
Since the two bubbles combine under isothermal condition (i.e., temperature remains constant), so Boyle's law holds good during the combination of bubbles. so,
P1V1+P2V2=P'V'
or (P+4sr1)43πr31+(P+4Sr2)43πr32
=(P+4Sr)43πr3
or (P+4sr1)πr31+(P+4Sr2)πr32
=(P+4Sr)πr3
or 4S(r21+r22+r2)=P(r3−r31−r32)
or S=P(r3−r31−r32)4(r21+r22−r2) Proved.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Conceptual Problems
Explore 103 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Advanced problems for competitions
Explore 21 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Long Answer questions
Explore 33 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A soap bubble of radius r si blown up to form of bubble of radius 3r under isothermal conditions . What is the energy spent in doing so if the surface tension of soap solution is S.
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View Solution
Knowledge Check
A soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
A3πσr2B6πσr2C12πσr2D24πσr2Two spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
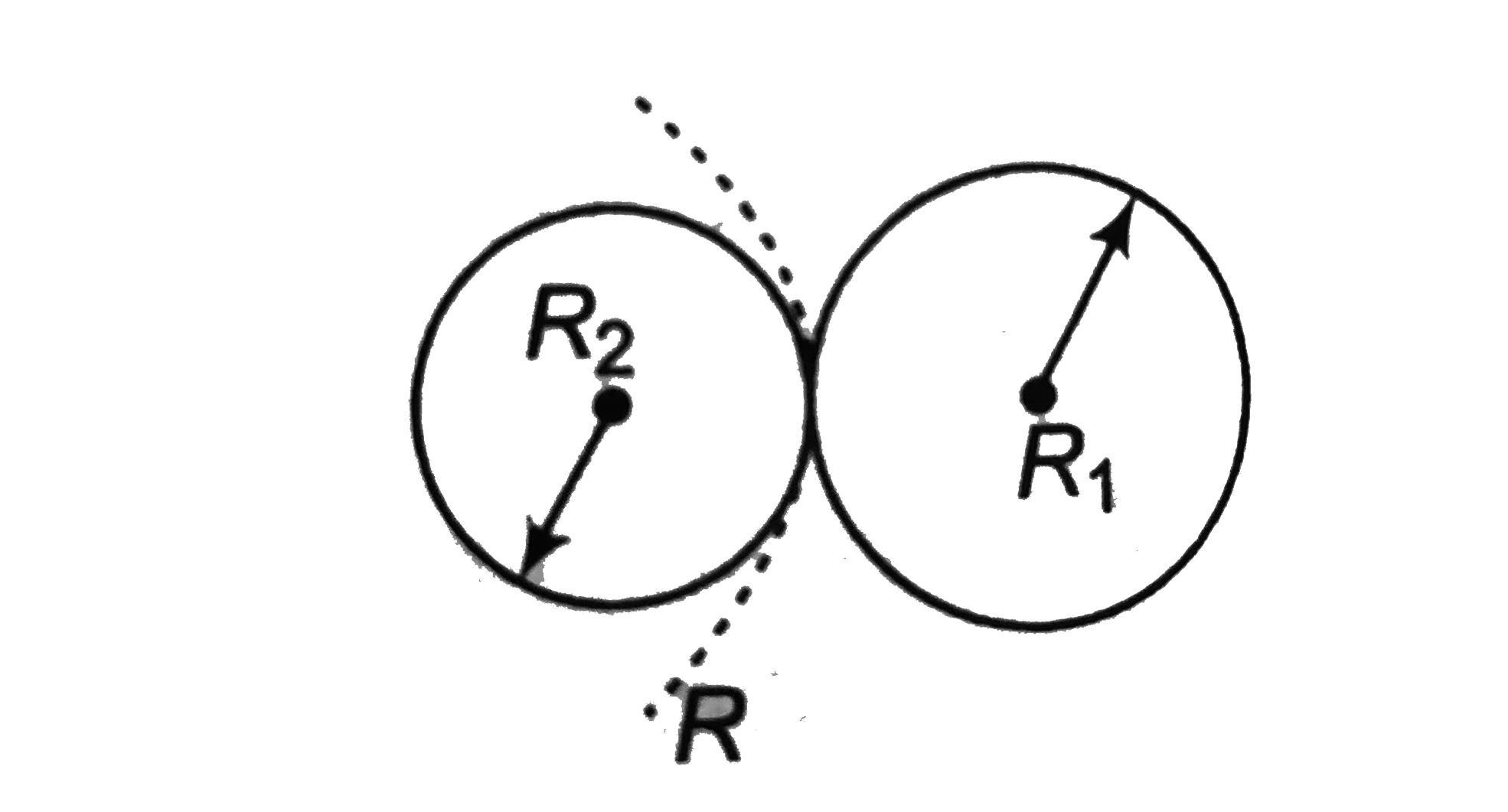 .AR=R1−R2BR=R1−R22C1R=1R2−1R1D1R=1R2+1R1
.AR=R1−R2BR=R1−R22C1R=1R2−1R1D1R=1R2+1R1
Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo soap bubbles of radius R1 and R2 combine isothermally to form a new soap bubble. Find radius of new soap bubble
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
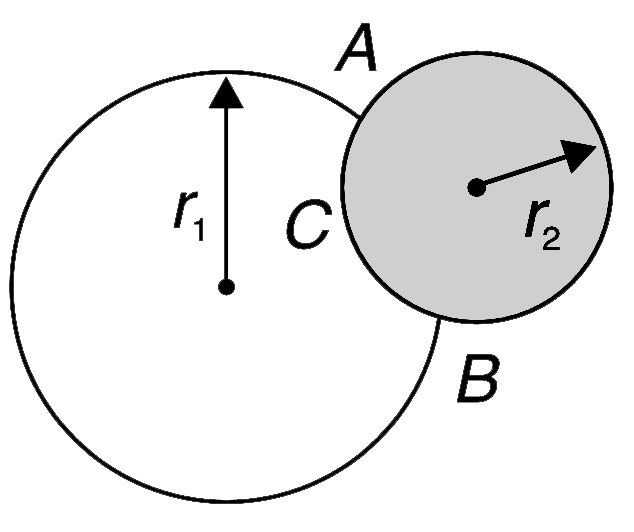
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionA soap bubble of radius R has formed at normal temperature and pressure under isothermal conditions. Complete the work done. The surface tension of soap solution is T.
View Solution

