A capillary tube of 2 mm diameter and 20 cm long is fitted horizontally to a vessel kept full of alcohol of density 0.8g/cm3. The depth of the centre of capillary tube below the free surface of alcohol is 30 cm. If viscosity of alchole is 0.112 poise, find the amount that will flow in 5 minutes.
Here, r=1mm=0.1cm,l=20cm,
ρ=0.8g/cm3,h=30cm,η=0.12poise
Volume of the alcohol that will be flowing per second through the capillary tube is
V=πPr48ηl=πhρgr48ηl
=227×30×0.8×980×(0.1)48×0.12×20=0.385cc/s
Volume flowing out in 5 minutes
=0.385×300=115.5cc
Mass of the liquid flowing out in 5 minutes
=115.5×0.8=92.4g.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Conceptual Problems
103 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions
21 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions
33 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A capillary tube of 1mm diameter and 20 cm long is fitted horizontally to a vessel kept full of alcohol of density 0.8 gm//c.c. The depth of centre of capillary tube below the surface of alcohol is 20 cm. If the visosity of oil is 0.12dynecm−2 s, find the amount of liquid that will flow in 5 minuts.
View SolutionA capillary tube of length 25 cm and diameter 0.1cm is fitted horizontally to a vessel full of a liquid of coefficient of visocity 0.012 cgs unit. The depth of the capillary tube below the surface of liquid is 15 cm. If the density of liquid is 0.8g/cm3, calculate the amount of the liquid that will flow out in 7 minutes. Take g=980cm/s2
View Solution
Knowledge Check
Alcohol of density 8×104kg/m3 and surface tension 22×10−3 N/m rises through a capillary tube of diameter 0.4×10−3 m . The vertical height to which the alcohol will rise is ,
A28×10−4,mB2.8×10−4C0.28×10−4mD0.28×10−4mWater rise in capillary tube when its one end is dipped vertically in it, is 3 cm. If the surface tension of water is 75×10−3Nm, then the diameter of capillary will be (Take angle of contact=0∘C)
A0.1mmB0.5mmC1.0mmD2.0mm
A soap bubble of radius 4 cm and surface tension 30 dyne cm−1 is blown at the end of a tube of length 10 cm and intenal radius 0.2cm If the viscosity of air is 1.89×10−4 poise, Find the time taken by the bubble to be reduced ota radius of 2 cm.
View SolutionThe inner diameter of a metallic tube of density 7gcm3 is 2.5 cm. The thickness of the tube is 0.29 cm. Find the weight of the tube, if it is of length 30cm.
View SolutionWater is flowing through a horizontal tube of radius 5 cm and length 5 cm at the rate of 30 lt/s. Find the pressure required to maintain the flow of water if coefficient of viscosity of water is 0.002 Pa s.
View SolutionA glass capillary tube of inner diameter 0.28mm is lowered verically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as that in the vessel is λ×105N/m2. Then find λ in nearest integer (surface tension of water =0.07N/m and atmospheric pressure =105N/m2) :
View SolutionA capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
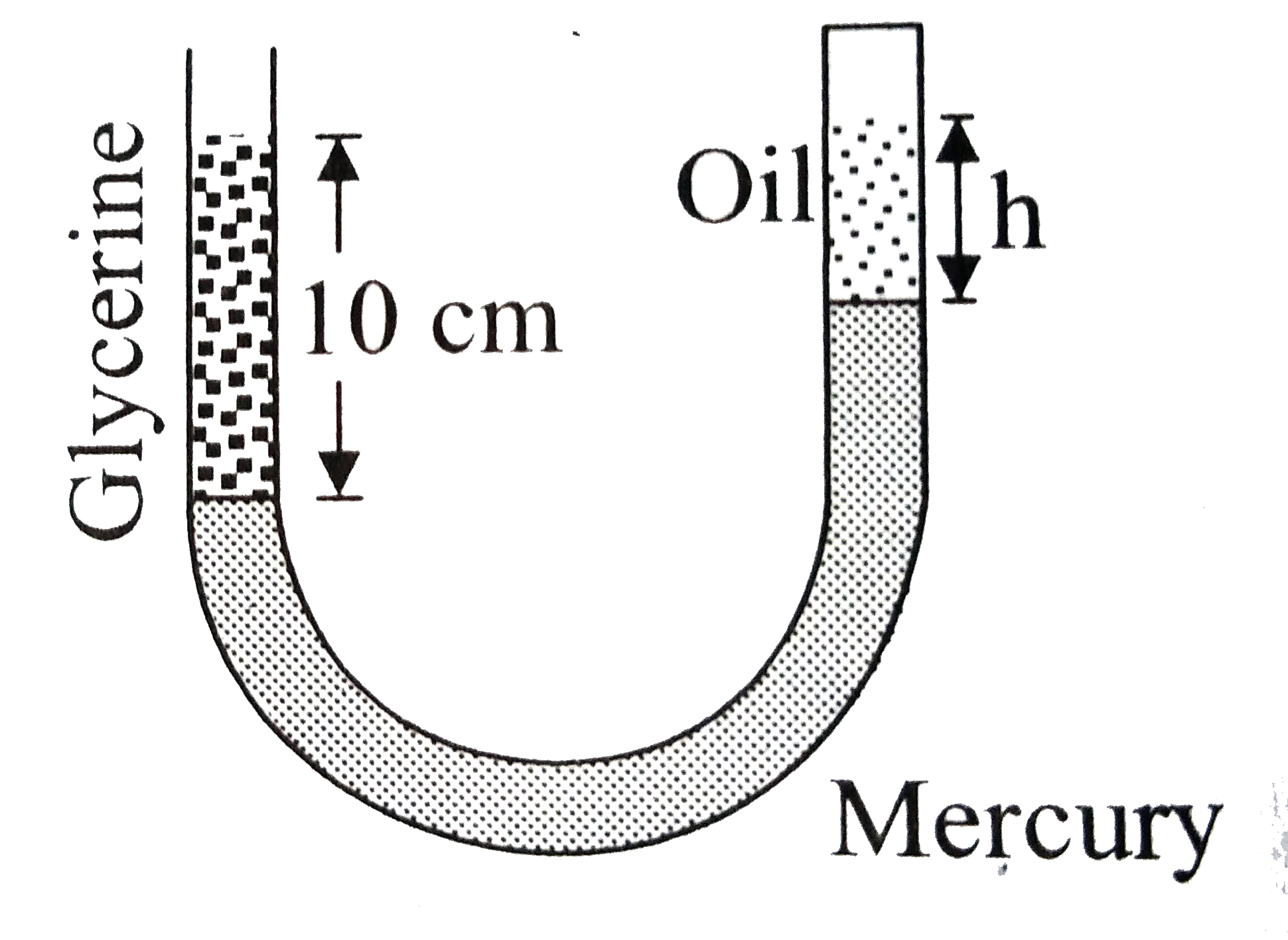
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
View Solution