A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
R/2
R/3
R/5
R/4
The correct Answer is:B
To solve the problem of finding the maximum height attained by a body projected vertically upwards from the surface of a planet with a velocity equal to half the escape velocity, we can follow these steps:
Step 1: Determine the Escape Velocity
The escape velocity ve for a planet of radius R and mass M is given by the formula:
ve=√2GMR
where G is the universal gravitational constant.
Step 2: Calculate the Initial Velocity
Since the body is projected with a velocity equal to half the escape velocity, we have:
v=12ve=12√2GMR=√GM2R
Step 3: Apply Conservation of Energy
We will use the conservation of mechanical energy to find the maximum height h attained by the body. The total mechanical energy at the surface of the planet (initial) is the sum of kinetic energy (KE) and gravitational potential energy (PE):
- Initial Kinetic Energy (KE):
KE=12mv2=12m(√GM2R)2=12m⋅GM2R=mGM4R
- Initial Potential Energy (PE):
PE=−GMmR
Thus, the total initial energy Ei is:
Ei=mGM4R−GMmR=mGM4R−4mGM4R=−3mGM4R
Step 4: Energy at Maximum Height
At the maximum height h, the kinetic energy will be zero, and the potential energy will be:
PE=−GMmR+h
The total energy Ef at maximum height is:
Ef=0−GMmR+h=−GMmR+h
Step 5: Set Initial Energy Equal to Final Energy
By conservation of energy, we set Ei=Ef:
−3mGM4R=−GMmR+h
Step 6: Solve for h
Cancelling GMm from both sides gives:
34R=1R+h
Cross-multiplying yields:
3(R+h)=4R
Thus,
3h=4R−3R=R⟹h=R3
Conclusion
The maximum height attained by the body is:
h=R3
The escape velocity ve for a planet of radius R and mass M is given by the formula:
ve=√2GMR
where G is the universal gravitational constant.
Since the body is projected with a velocity equal to half the escape velocity, we have:
v=12ve=12√2GMR=√GM2R
We will use the conservation of mechanical energy to find the maximum height h attained by the body. The total mechanical energy at the surface of the planet (initial) is the sum of kinetic energy (KE) and gravitational potential energy (PE):
- Initial Kinetic Energy (KE):
KE=12mv2=12m(√GM2R)2=12m⋅GM2R=mGM4R
- Initial Potential Energy (PE):
PE=−GMmR
Ei=mGM4R−GMmR=mGM4R−4mGM4R=−3mGM4R
At the maximum height h, the kinetic energy will be zero, and the potential energy will be:
PE=−GMmR+h
The total energy Ef at maximum height is:
Ef=0−GMmR+h=−GMmR+h
By conservation of energy, we set Ei=Ef:
−3mGM4R=−GMmR+h
Cancelling GMm from both sides gives:
34R=1R+h
Cross-multiplying yields:
3(R+h)=4R
Thus,
3h=4R−3R=R⟹h=R3
The maximum height attained by the body is:
h=R3
Similar Questions
A body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View SolutionA body is projected vertically upward from. the surface of the earth.with a velocity equal to half its escape velocity. If R is radius of the earth, then the maximum height attained by the,body is (Rn). Find n.
View Solution
Knowledge Check
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/9A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A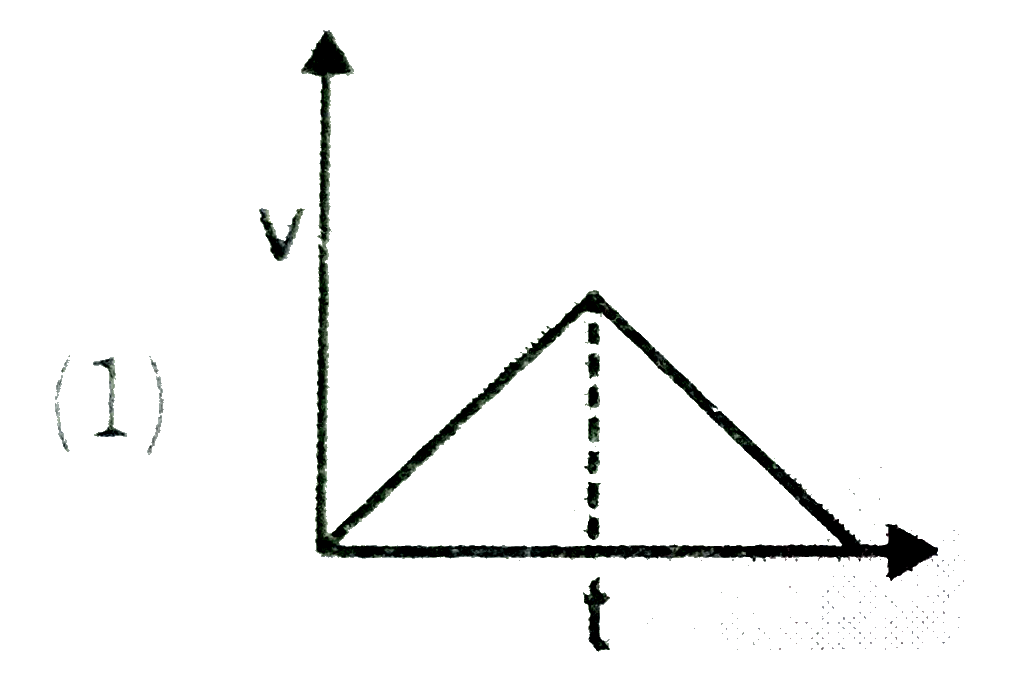 B
B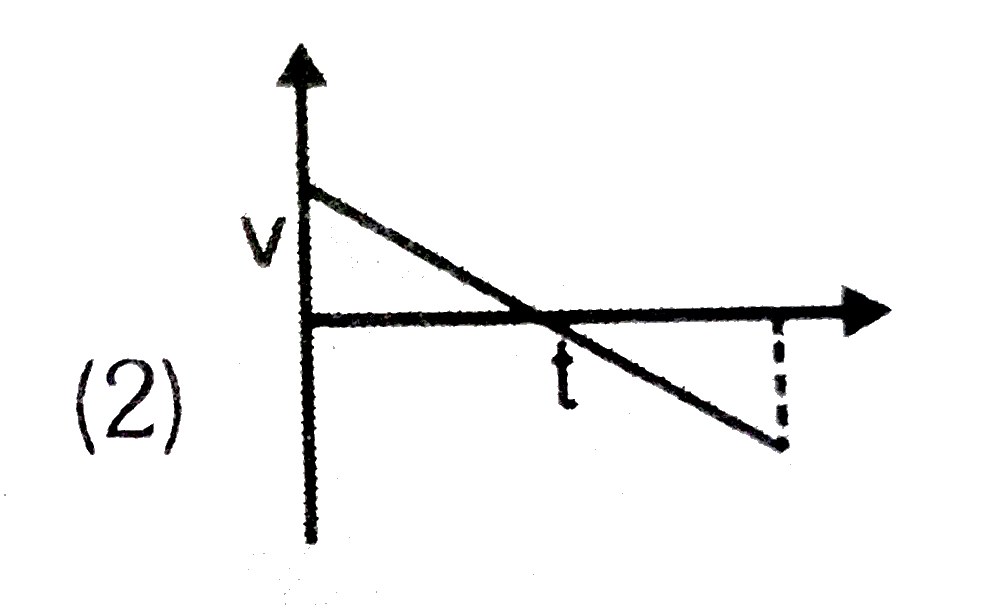 C
C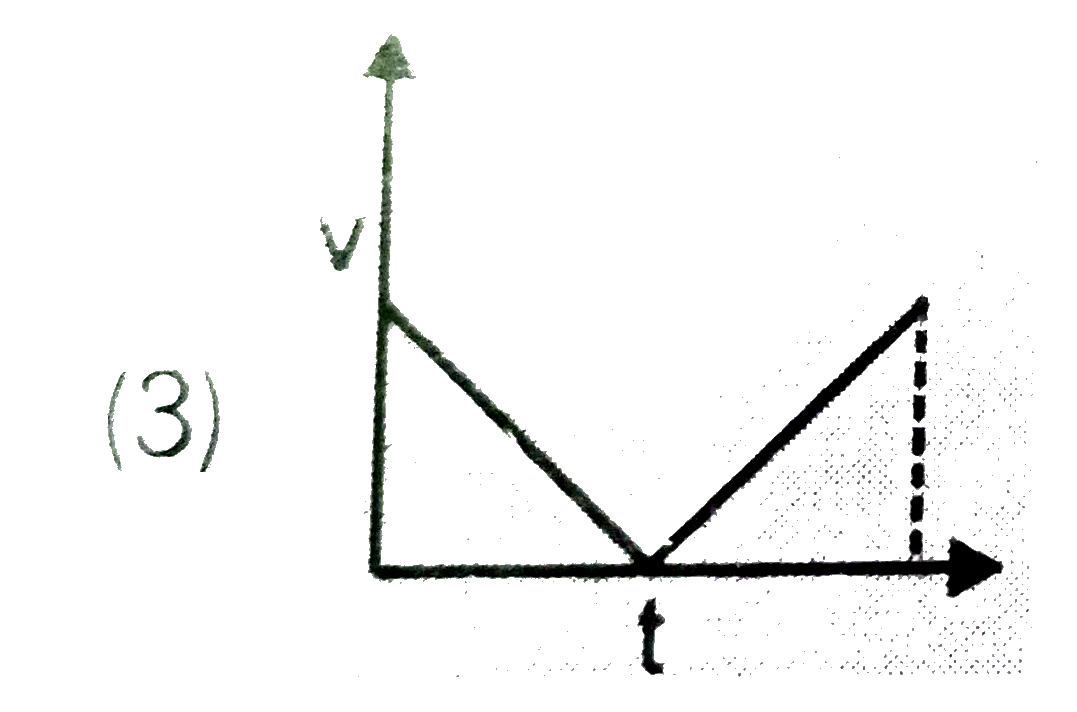 D
D
There is crater of depth R/100 on the surface of the moon (raduis R). A projectile is fired vertically upwards from the crater with a velocity, which is equal to the escape velocity v from the surface of the moon. The maximum height attained by the projectile, is :
A90RB95RC99.5RD50R
A body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA particle is projected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionA particle is projected vertically upward the surface of the earth (radius Re ) with a speed equal to one-fourth of escape velocity. The maximum height attained by it from the surface of the earth is Rek. Find k.
View SolutionA particle is prjected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionA body is projected horizontally from the surface of the earth (radius =R) with a velocity equal to n times the escape velocity. Neglect rotational effect of the earth. The maximum height attained by the body from the earth s surface is R/2. Then, n must be
View Solution

