Find out the degeneracy of hydrogen atom that has the erngy equal to −RH9 (RH = Rydberg costant ).
The correct Answer is:9
Energy in H-atom −RHn2=−RH9
∴N=3
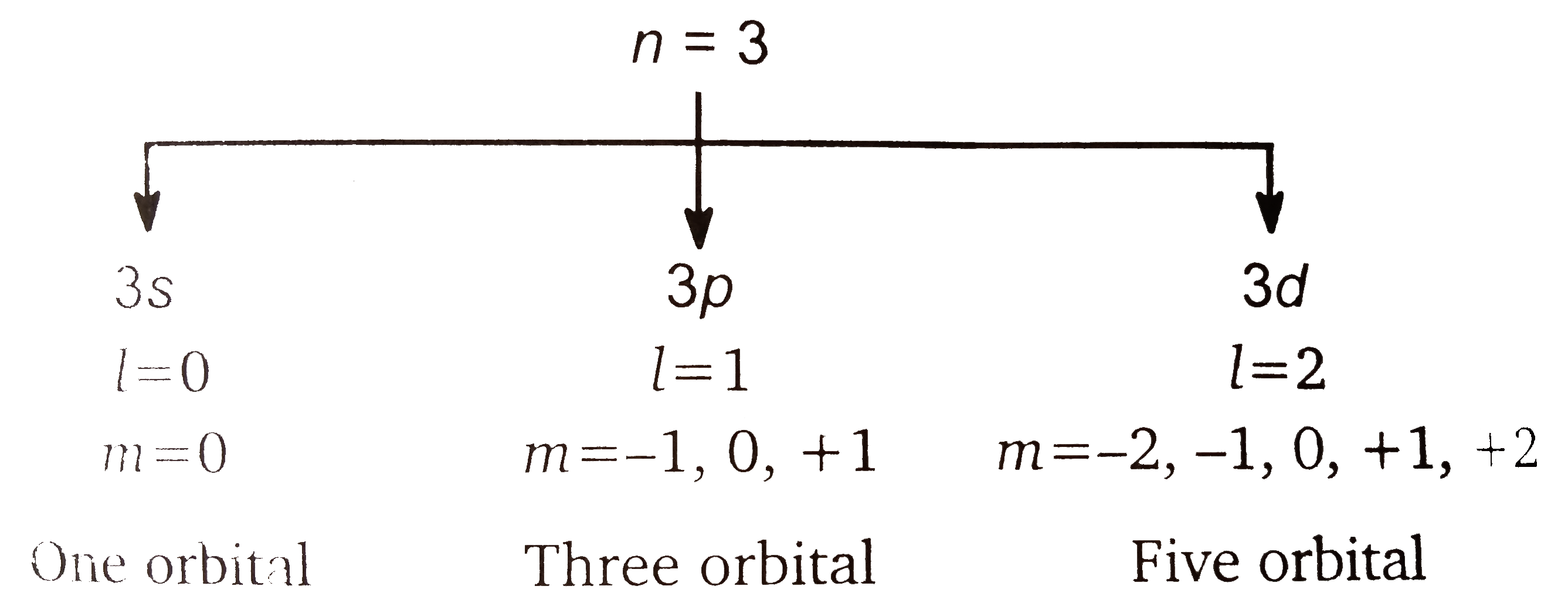
degeneracy =1+3+5=9 .
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 7
33 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 8
19 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 4
39 Videos
- CHEMICAL BONDINGBOOK - P BAHADURCHAPTER - CHEMICAL BONDINGEXERCISE - Exercise 7
11 Videos
Similar Questions
Using Bohr's postulates, derive the expression for the total energy of the electron revolving in nth orbit of hydrogen atom. Find the wavelength of Hα line, given the value of Rydberg constant, R=1.1×107m1
View SolutionAs per Bohr's theory of hydrogen atom the value of Rydberg constant R is ______.
View Solution
Knowledge Check
An electron makes a transition from orbit n=4 to the orbit n=2 of a hydrogen atom. The wave number of the emitted radiations (R= Rydberg's constant) will be
A163RB2R16C3R16D4R16An electron makes a transition from orbit n=4 to the orbit n=2 of a hydrogen atom. The wave number of the emitted radiation (R=Rydberg's cosntant) will be
A163RB2R16C3R16D4R16The Rydberg constant R for hydrogen is
AR=−(14πε0).2π2me2ch2BR=(14πε0).2π2me4ch2CR=(14πε0)2.2π2me4c2h2DR=(14πε0)2.2π2me4ch3
What is the recoil velocity of Hydrogen atom when a photon is emitted due to corresponding transition from n=5 to n=1. (RH = Rydberg's constant, mH, = mass of hydrogen)
View SolutionRydberg constant R is equal to
View SolutionA stationary hydrogen atom emits photon corresponding to the first line of Lyman series. If R is the Rydberg constant and M is the mass of the atom, then the velocity acquired by the atom is
View SolutionWhat is the lowest energy of the spectral line emitted by the hydrogen atom in the Lyman series?
(h = Planck's constant, c = velocity of light, R = Rydberg's constant).
View SolutionThe first emission line of Balmer series in He+ - spectrum has the wave no .in (Cm_1) (R-Rydberg constant)
View Solution