In order to coincide the parabolas formed by singly ionized ions in one spectrograph and doubly ionized ions in the other Thomson's mass spectrograph , the electric fields and magnetic fields are kept in the ratios $1 : 2$ and $3 : 2$ respectively . Then the ratio of masses of the ions is

A

$3 : 4$

B

$1 : 3$

C

$9 : 4$

D

None of thses

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Using $Z^{2} = k (\frac{q}{m}) y$ , where $k = \frac{B^{2} L D}{E}$
For parabolas to coincide in the two photographs , the
$\frac{k q}{m}$ should be same for the two cases . Thus ,
$\frac{B_{1}^{2} L D e}{E_{1} m_{1}} = \frac{B_{2}^{2} L D (2 e)}{E_{2} m_{2}}$
$\Rightarrow \frac{m_{1}}{m_{2}} = {(\frac{B_{1}}{B_{2}})}^{2} \times (\frac{E_{2}}{E_{1}}) \times \frac{1}{2} = \frac{9}{4} \times \frac{2}{1} \times \frac{1}{2} = \frac{9}{4}$

|

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Electric field and magnetic field in Thomson mass spectrograph are applied
ASimultaneously, perpendicular
BPerpendicular but not simultaneously
CParallel but no simultaneously
DParallel simultaneously
Question 2 - Select One
Two particles having same charge and $K E$ enter at right angles into the same magnetic field and travel in circular paths of radii $2 c m$ and $3 c m$ respectively. The ratio of their masses is .
A $2 : 3$
B $3 : 2$
C $4 : 9$
D $9 : 4$
Question 3 - Select One
In a parabola spectrograph, the velocities of four positive ions P,Q,R and S are $v_{1}, v_{2}, v_{3}$ and $v_{4}$ respectively

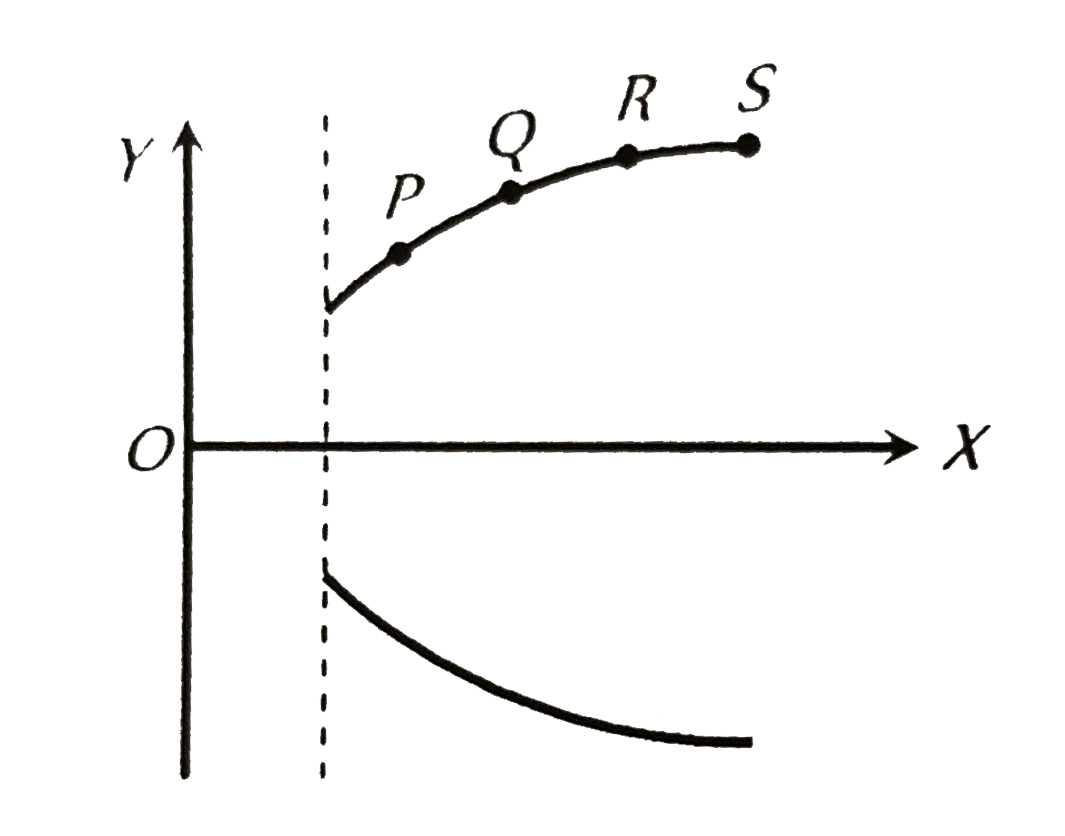A $v_{1} > v_{2} > v_{3} > v_{4}$
B $v_{1} < v_{2} < v_{3} < v_{4}$
C $v_{1} = v_{2} = v_{3} = v_{4}$
D $v_{1} < < v_{2} > v_{3} < v_{4}$

A2Z-DUAL NATURE OF RADIATION AND MATTER-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile