When a charged particle with charge q and mass m enters uniform magnetic field B with velocity v at right angles to B, the force on the moving particle is given by qvB. This force acts as the centripetal force making the charged particle go in a uniform circular motion with radius r=mvBq
Now if a hydrogen ion and a deuterium ion enter the magnetic field with velocities in the ratio 2:1 respectively, then the ratio of their radii will be -
1:2
2:1
1:4
1:1
The correct Answer is:D
To solve the problem, we need to find the ratio of the radii of the circular motion of a hydrogen ion and a deuterium ion when they enter a uniform magnetic field with given velocities.
1. Understanding the Formula for Radius:
The radius r of the circular motion of a charged particle in a magnetic field is given by the formula:
r=mvBq
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- B is the magnetic field strength,
- q is the charge of the particle.
2. Identifying the Particles:
We have two particles:
- Hydrogen ion (H+) with mass mH.
- Deuterium ion (D+) with mass mD=2mH (since deuterium has one proton and one neutron).
3. Given Velocity Ratio:
The velocities of the hydrogen and deuterium ions are given in the ratio:
vH:vD=2:1
This means vH=2v and vD=v for some velocity v.
4. Calculating the Radii:
- For the hydrogen ion:
rH=mHvHBqH=mH(2v)BqH=2mHvBqH
- For the deuterium ion:
rD=mDvDBqD=(2mH)vBqD=2mHvBqD
5. Finding the Ratio of Radii:
We need to find the ratio rHrD:
rHrD=2mHvBqH2mHvBqD=qDqH
Since both hydrogen and deuterium ions have the same charge (q), we have:
rHrD=1
6. Conclusion:
The ratio of the radii of the hydrogen ion to the deuterium ion is:
rHrD=1
Final Answer:
The ratio of their radii is 1:1.
The radius r of the circular motion of a charged particle in a magnetic field is given by the formula:
r=mvBq
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- B is the magnetic field strength,
- q is the charge of the particle.
We have two particles:
- Hydrogen ion (H+) with mass mH.
- Deuterium ion (D+) with mass mD=2mH (since deuterium has one proton and one neutron).
The velocities of the hydrogen and deuterium ions are given in the ratio:
vH:vD=2:1
This means vH=2v and vD=v for some velocity v.
- For the hydrogen ion:
rH=mHvHBqH=mH(2v)BqH=2mHvBqH
- For the deuterium ion:
rD=mDvDBqD=(2mH)vBqD=2mHvBqD
We need to find the ratio rHrD:
rHrD=2mHvBqH2mHvBqD=qDqH
Since both hydrogen and deuterium ions have the same charge (q), we have:
rHrD=1
The ratio of the radii of the hydrogen ion to the deuterium ion is:
rHrD=1
The ratio of their radii is 1:1.
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
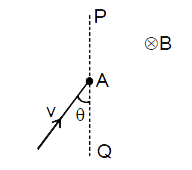
time spentView SolutionA charged particle having charge q is moving in a uniform magnetic field B parallel to the lines of field force, the magnetic force acting on a charge will be qvB
View Solution
Knowledge Check
- Question 1 - Select One
If a charged particle enters perpendicular in the uniform magnetic field then
AEnergy remains constant but moment changesBEnergy and momentum both remains constantCMomentum remains constant but energy changesDNeither energy nor momentum remains constant - Question 2 - Select One
The force acting on a particle of charge q moving in a uniform magnets field with velocity v is
Aparallel to both →v and →BBperpendicular to both →v and →BCparallel to →v and perpendicular to →BDperpendicular to →v and parallel to →B - Question 3 - Select One
A charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqB
When a charged particle enters a uniform magnetic field its kinetic energy
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA charged particle enters in a uniform magnetic field with a certain velocity. The power delivered to the particle by the magnetic field depends on
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View Solution
