A particle of specific charge qm=πC/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆkT. The velocity →v of particle after time t=112s will be (in m/s)
5[ˆi+√3ˆj]
5[√3ˆi+ˆj]
5[√3ˆi−ˆj]
5[ˆi+ˆj]
The correct Answer is:B
Time period T=2πmqB
T=2ππ×2=1s
Thus particle will beat point P after t=112s.
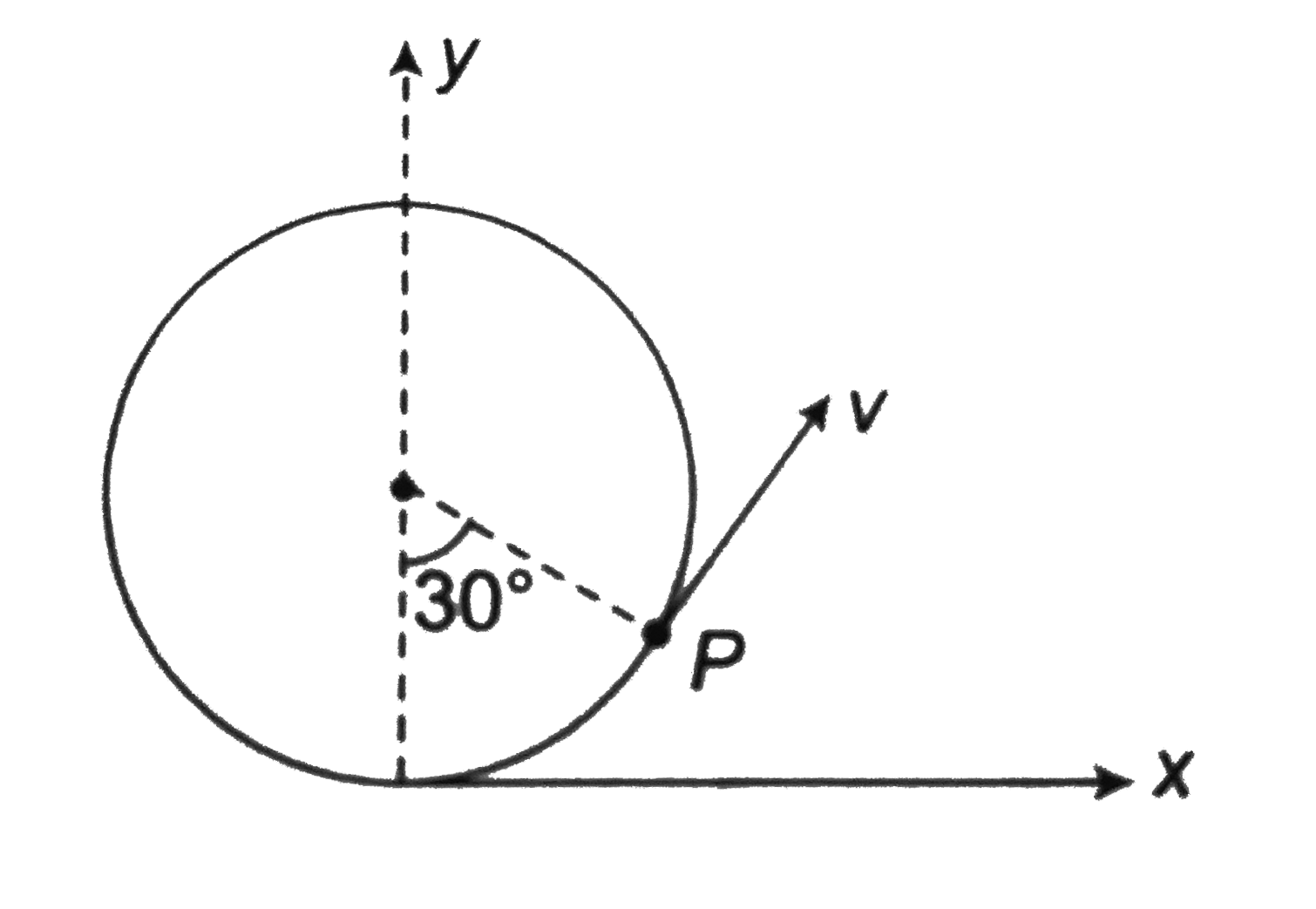
→v=10[cos30ˆi+sin30ˆj]
→v=10[√32ˆi+12ˆj]=5[√3ˆi+ˆj]m/s
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions
47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View Solution
Knowledge Check
A particle of specific charge q/m=(π)C/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆK Tesla. The velocity →V of the particle after time t=1/6 s will be
A(5ˆi+5√3ˆj)m/sB10ˆjm/sC(5√3ˆi+5ˆj)m/sD−10ˆjm/sA particle of specific charge qm=πCkg−1 is projected from the origin toward positive x-axis with a velocity of 10ms−1 in a uniform magnetic field →B=−2ˆkT. The velocity →v of particle after time t=112s will be (in ms−1)
A5[ˆi+√3ˆj]B5[√3ˆi+ˆj]C5[√3ˆi−ˆj]D5[ˆi+ˆj]A charged particle of specific charge (charge/mass) α released from origin at time t=0 with velocity →v=v0(ˆi+ˆj) in uniform magnetic field →B=B0ˆi. Coordinates of the particle at time t=π/(B0α) are
A(v02B0α,√2v0αB0,−v0B0α)B(v02B0α,0,0)C(0,2v0B0α,v0π2B0α)D(v0πB0α,0,−2v0B0α)
What is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionA particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=πm2qB.
View SolutionIn a right handed coordinate system XY plane is horizontal and Z-axis is vertically npward. A uniform magnetic field exist in space in vertically npward direction with magnetic induction B. A particle with mass m and charge q is projected from the origin of the coordinate system at t=0 with a velocity vector given as
→v=v1ˆi+v2ˆk
Find the velocity vector of the particle after time t.
View SolutionA charge particle moves with velocity →V in a uniform magnetic field →B . The magnetic force experienced by the particle is
View SolutionThe electric field acts positive x-axis. A charged particle of charge q and mass m is released from origin and moves with velocity →v=v0ˆj under the action of electric field and magnetic field, →B=B0ˆi. The velocity of particle becomes 2v0 after time √3mv0√2qE0. find the electric field:
View Solution
