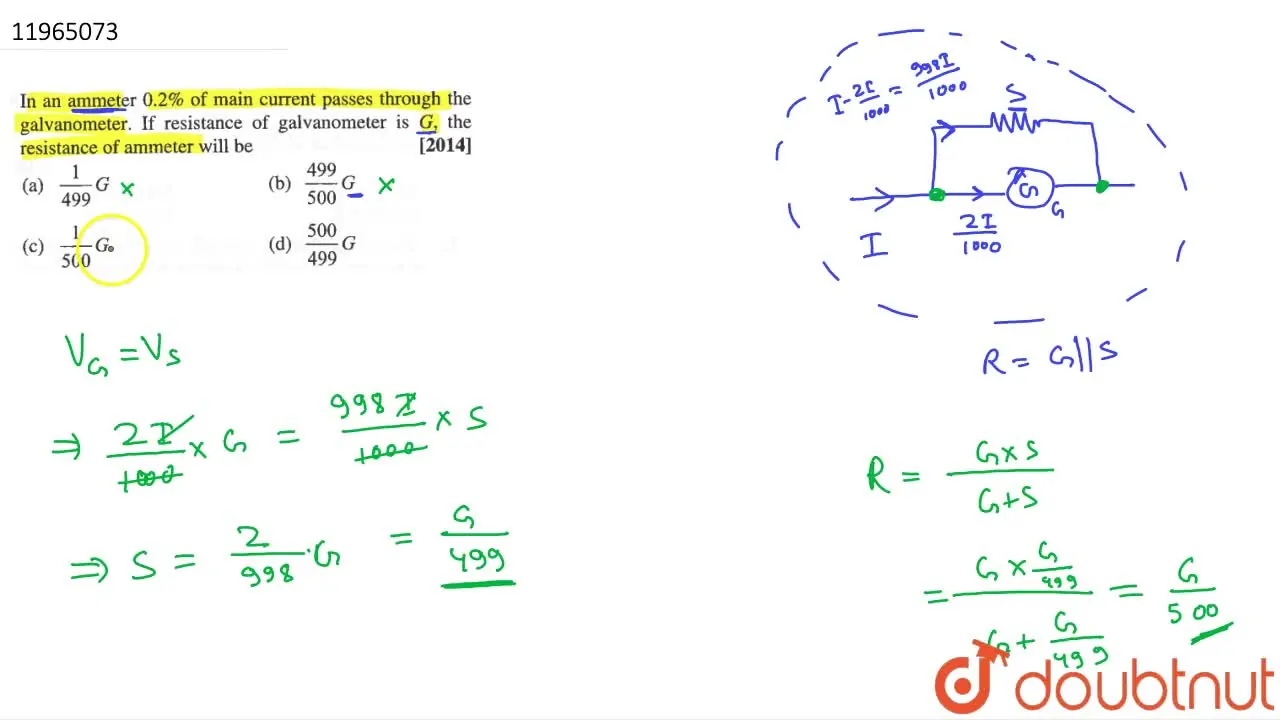
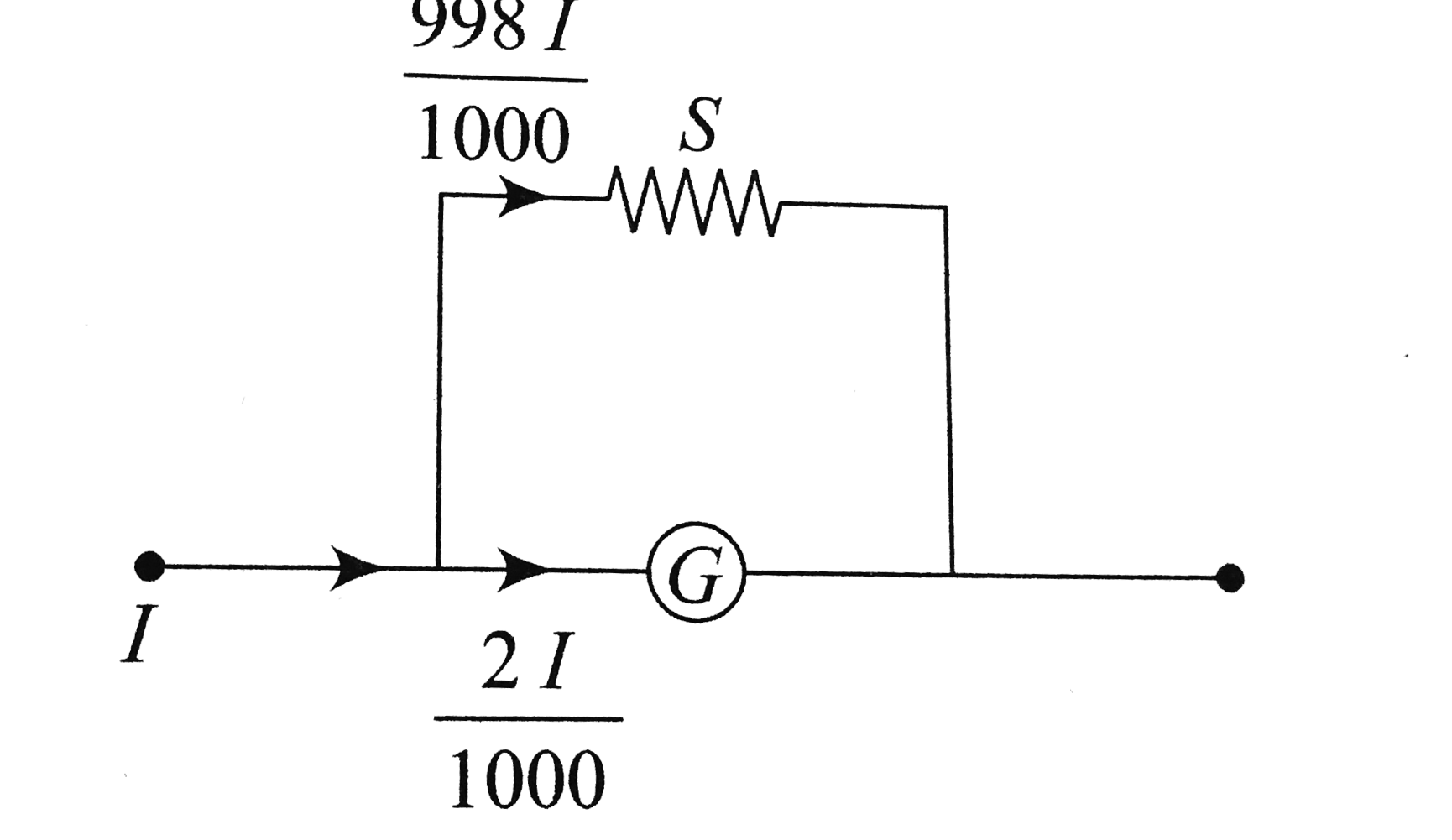
In a ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
1499G
499500G
1500G
500499G
The correct Answer is:C
(c ) As 0.2% of main current passes through the galvanometer, hence 9981000I current through the shunt.
2I100
(2I1000)G=(998I1000)S⇒G499
Total resistance of ammeter
R=SGS+G=(G499)G(G499)+G=G500
Related Playlists
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section - C1videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - AIIMS Questions36videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section B - Assertion Reasoning28videos
CURRENT ELECTRICITY
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test30videos
ATOMIC PHYSICS
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
In an ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
View SolutionIn an ammeter 0⋅2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
View SolutionIn a ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
View SolutionIn a ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
View SolutionIn an ammeter 5% of the main current is passing through the galvanometer. If the resistance of galvanometer is G, then the resistance of shunt S will be
View SolutionIn an ammeter 10% of main current is passing through the galvanometer. If the resistance of the galvanometer is G, then the shunt resistance, in ohms is
View SolutionIn an ammeter, 4% of the main current is passing through the galvanometer. If shunt resistance is 5 Ω, then resistance of galvanometer will be
View SolutionAssertion : In a shunted galvanometer, only 10% current passes through the galvanometer. The resistance of the galvanometer is G. Then resistance of the shunt is G/9.
Reason : If S is the shunt, then voltage across S and G is same.View SolutionIn an ammeter, 4% of the main current is passing through the galvanometer. If shunt resistance is 5 Ω, then resistance of galvanometer will be
View SolutionIf 2% current passes through galvanometer. Shunt resistance is 5 ohms then resistance of galvanometer is what?
View Solution