If the wire has resistively per unit area of cross-section.the resistance between A and B is
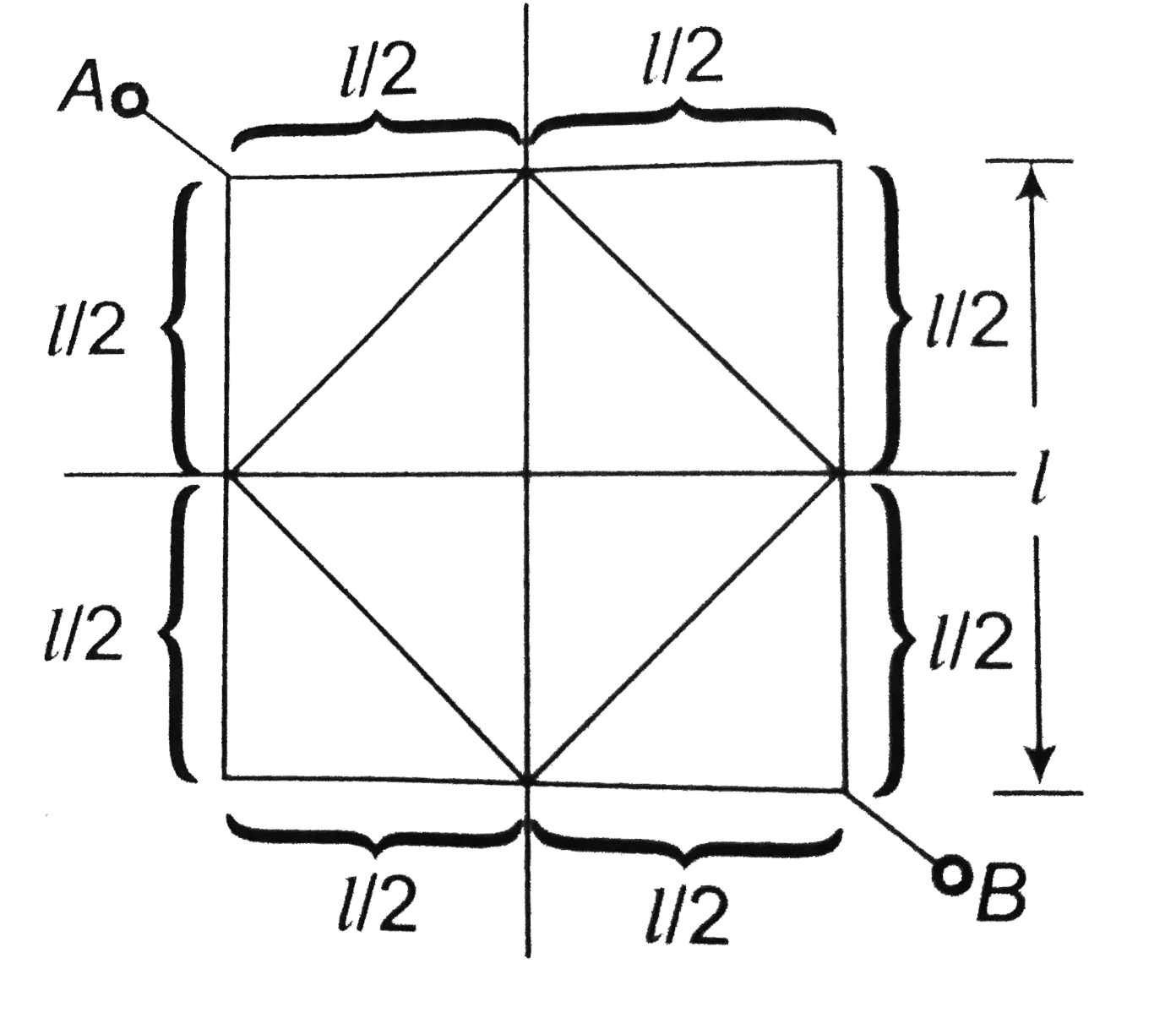
ρl√2
√2ρl
2ρl
none of these
The correct Answer is:A
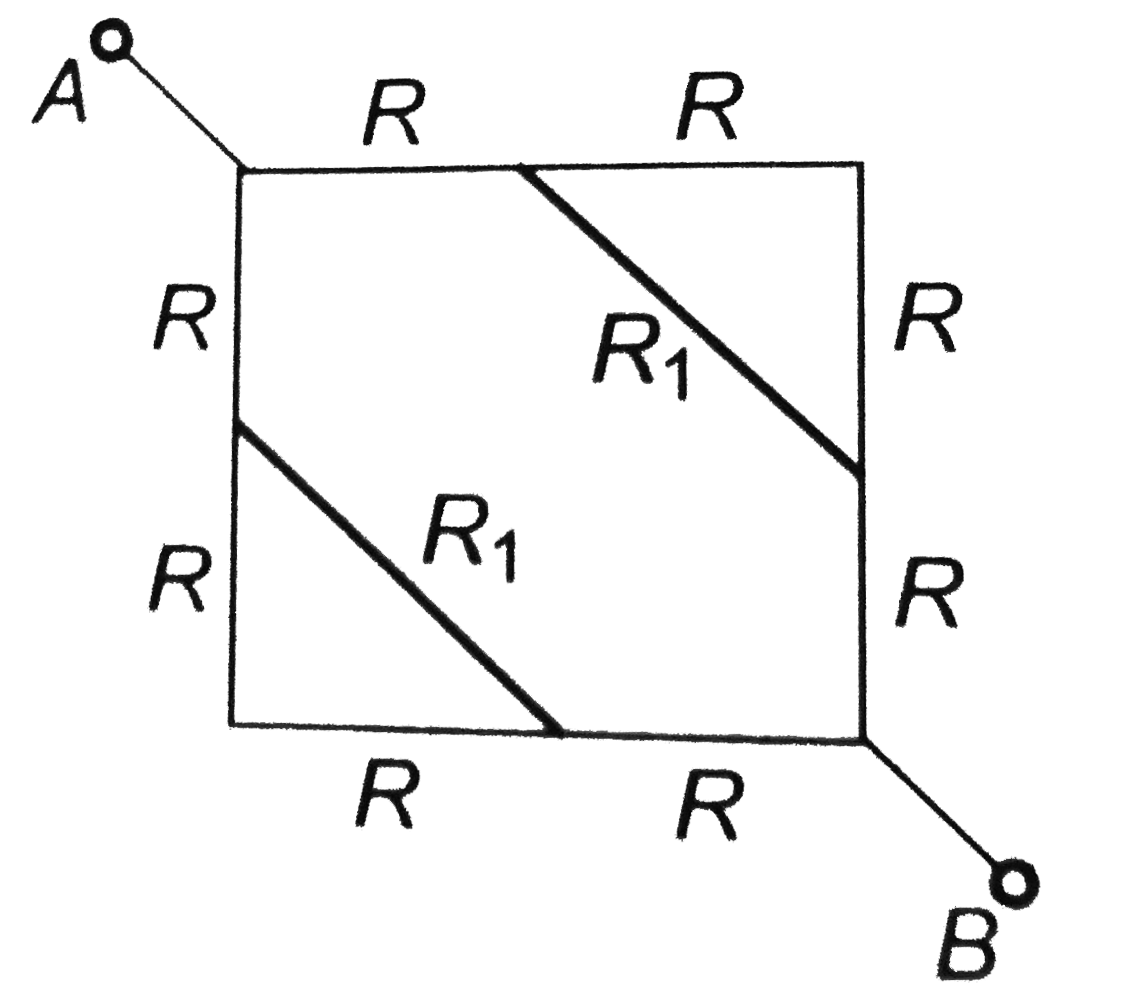
(a) The figure can be redrawn as :
R=ρl2
R1=ρl√2
Req=12[2RR12R+R1=2R]=ρl√2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section - A
1 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section B - Assertion Reasoning
28 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Heating Effect Of Current
40 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Two wires are of same length and same area of cross-section. If first wire has resistivity ρ1 and temperature coefficient of resistance α1 but second wire has resistivity ρ2 and temperature coefficient of resistance α2. Their series equivalent resistance is independent of small temperature changes. Then
View SolutionThe specific resistance and area of cross section of the potentiometer wire are ρ' and A respectively. If a current i passes through the wire, its potential gradient will be
View Solution
Knowledge Check
The specific resistance per unit area of cross section of a wire is equivalent to –
Acharge/currentBresistance/lengthCpotential gradientDcurrent/areaBraking froce per unit area of cross section of a wire is called
Ayield pointBtensile stressCductilityDbreaking stressA battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
Abe halvedBbe doubledCbecome zeroDremain unchanged
A wire of resistance 4Ω is stretched to twice its original length. In the process of stretching, its area of cross-section gets halved. Now, the resistance of the wire is
View SolutionTwo copper wires A and B of length l and 2l respectively, have the same area of cross-section. The ratio of the resistivity of wire A to the resistivity of wire B is
View SolutionIf the resistivity of a potentiometer wire be ρ and area of cross-section be A , then what will be potential gradient along the wire
View SolutionWhen length of a metal wire is doubled and area of cross-section is reduced to half, then its resistance becomes
View SolutionWhen the length and area of cross-section both are doubled, then its resistance
View Solution
