How much kinetic energy will be gained by an particle in going from a point at to another point at
The correct Answer is:A
To find the kinetic energy gained by an alpha particle when moving from a point at 70 V to another point at 50 V, we can follow these steps:
Step 1: Understand the concept of potential difference
The kinetic energy gained by a charged particle moving through a potential difference is equal to the work done on the particle by the electric field. This work done can be calculated using the formula:
Work Done=Charge×Potential Difference
Step 2: Identify the charge of the alpha particle
An alpha particle consists of 2 protons and 2 neutrons. The charge of a proton is approximately e=1.6×10−19 coulombs. Therefore, the total charge Q of an alpha particle is:
Q=2×e=2×1.6×10−19C=3.2×10−19C
Step 3: Calculate the potential difference
The potential difference ΔV that the alpha particle moves through is:
ΔV=Vinitial−Vfinal=70V−50V=20V
Step 4: Calculate the work done (or kinetic energy gained)
Using the formula for work done:
Work Done=Q×ΔV
Substituting the values we have:
Work Done=(2×e)×(20V)
=2×(1.6×10−19C)×(20V)
=2×1.6×20×10−19
=64×10−19J
Since 1eV=1.6×10−19J, we can convert this to electron volts:
Kinetic Energy=64×10−19J1.6×10−19J/eV=40eV
Final Answer
The kinetic energy gained by the alpha particle is 40 eV.
---
The kinetic energy gained by a charged particle moving through a potential difference is equal to the work done on the particle by the electric field. This work done can be calculated using the formula:
Work Done=Charge×Potential Difference
An alpha particle consists of 2 protons and 2 neutrons. The charge of a proton is approximately e=1.6×10−19 coulombs. Therefore, the total charge Q of an alpha particle is:
Q=2×e=2×1.6×10−19C=3.2×10−19C
The potential difference ΔV that the alpha particle moves through is:
ΔV=Vinitial−Vfinal=70V−50V=20V
Using the formula for work done:
Work Done=Q×ΔV
Substituting the values we have:
Work Done=(2×e)×(20V)
=2×(1.6×10−19C)×(20V)
=2×1.6×20×10−19
=64×10−19J
Since 1eV=1.6×10−19J, we can convert this to electron volts:
Kinetic Energy=64×10−19J1.6×10−19J/eV=40eV
The kinetic energy gained by the alpha particle is 40 eV.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor
32 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor With Dielectric
32 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
The kinetc energy of a chargd particle decreased by 10 J as it moves from a point at potential 100 V to a point at potential 200V . Find the charge on the particle.
View SolutionA particle is projected from point A perpendicular to inclined plane with a velocity 50m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Time taken by particle in going from point A to point B is
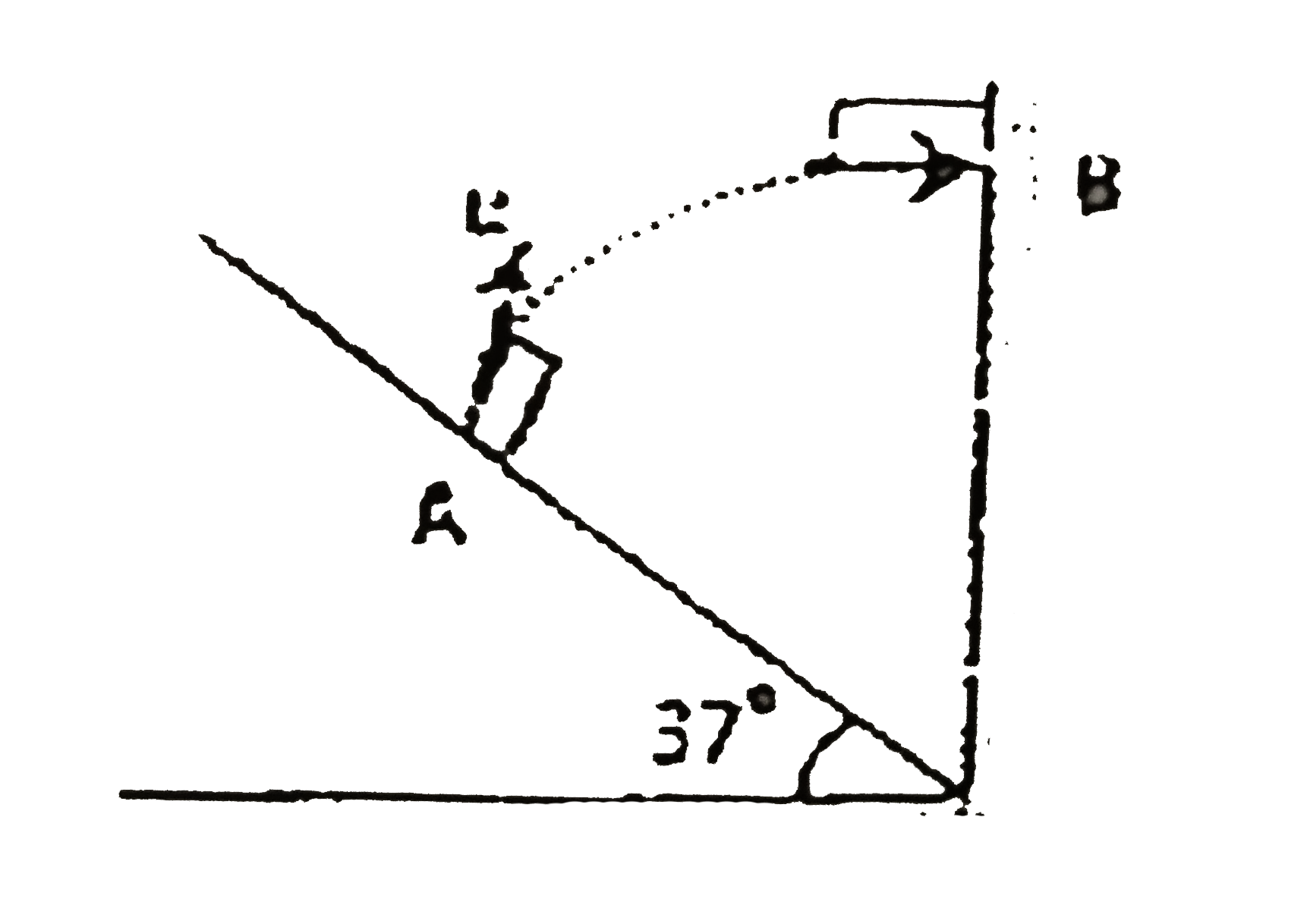
View Solution
Knowledge Check
In the Q.122 how much distance is covered by the particle in returning to the starting point?
A2r0aBr0aCr02aDr04aA particle moves on a path as shown. The particle takes 10 seconds in going from starting point to the final point. What is the average velocity vector of the particle ?
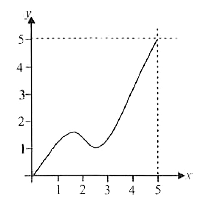 A0.5ˆi+ˆjB0.5ˆi+2.5ˆjC0.5ˆi+0.5ˆjDNone of these
A0.5ˆi+ˆjB0.5ˆi+2.5ˆjC0.5ˆi+0.5ˆjDNone of theseA particle is exeuting SHM. At a point x=A/3, kinetic energy of the particle of the particle is K, where A is the particle At a point x=2A/3, kinetic energy of the particle will be:
A2KBK√2C58KD53K
If 20J of work has to be done to move an electric charge of 4C from a point, where potential is 10V to another point, where potential is V volt, find the value of v.
View SolutionAn α-particle after passing through a potential difference of 2×106V falls on a silver foil. The atomic number of silver is 47. Calculaye (i) the kinetic energy of the α-particle at the time of falling on the foil (ii) the kinetic energy of the α-particle at a distance of 5×10−14 m from the nucleus and (iii) the shortest distance from the nucleus of silver to which the α-particle reaches.
View SolutionFigure (a) and (b) show the field lines of a positive and negative point charge respectively.
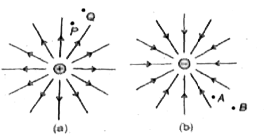
(a) Give the signs of the potential difference . Vp−VQ,VB−VA
(b) Give the sign of the potential energy difference if a small negative charge is moved from points Q to P from point A to B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
( d) Give the sign of the work done by the external agency in moving a samall negative charge from B to A .
(e ) Does the kinetic energy of a small negative charge increase or decrease in going from B to A ?
View SolutionIn one experiment , a proton having kinetic energy of 1 eV is accelerated through a potential difference of 3 V. In another experiment, an α-particle having initial kinetic energy 20 eV is retarded by a potential difference of 2 V. Calculate the ratio of de-Broglie wavelengths of proton and α - particle.
View SolutionThe potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with coordinates (3,3), only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates (1,1) is
View Solution
