A sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
54e.s.u.
14e.s.u.
30e.s.u.
36e.s.u.
The correct Answer is:D
To find the charge on the inner sphere, we can follow these steps:
Step 1: Understand the configuration
We have an inner sphere of radius r1=4cm charged to a potential of V=3e.s.u. and an outer hollow sphere of radius r2=6cm which is earthed (grounded).
Step 2: Use the formula for electric potential
The potential V at the surface of a charged sphere can be expressed as:
V=kQr
where k is a constant (Coulomb's constant), Q is the charge on the sphere, and r is the radius of the sphere.
Step 3: Set up the equation for the inner sphere
For the inner sphere, we can write:
3=kQ4
Here, Q is the charge on the inner sphere.
Step 4: Rearrange to find Q
Rearranging the equation gives:
Q=3⋅4/k
Since we are working in electrostatic units (e.s.u.), we can take k=1 for simplicity in this context:
Q=3⋅4=12e.s.u.
Step 5: Consider the effect of the outer sphere
The outer sphere is earthed, meaning it will have a charge induced on it to maintain a potential of zero. The charge on the outer sphere will be equal and opposite to the charge on the inner sphere. Thus, the outer sphere will have a charge of −Q.
Step 6: Calculate the total charge
Since the inner sphere has a charge of Q=12e.s.u., the charge on the inner sphere is:
Q=12e.s.u.
Final Answer
The charge on the inner sphere is 12e.s.u..
---
We have an inner sphere of radius r1=4cm charged to a potential of V=3e.s.u. and an outer hollow sphere of radius r2=6cm which is earthed (grounded).
The potential V at the surface of a charged sphere can be expressed as:
V=kQr
where k is a constant (Coulomb's constant), Q is the charge on the sphere, and r is the radius of the sphere.
For the inner sphere, we can write:
3=kQ4
Here, Q is the charge on the inner sphere.
Rearranging the equation gives:
Q=3⋅4/k
Since we are working in electrostatic units (e.s.u.), we can take k=1 for simplicity in this context:
Q=3⋅4=12e.s.u.
The outer sphere is earthed, meaning it will have a charge induced on it to maintain a potential of zero. The charge on the outer sphere will be equal and opposite to the charge on the inner sphere. Thus, the outer sphere will have a charge of −Q.
Since the inner sphere has a charge of Q=12e.s.u., the charge on the inner sphere is:
Q=12e.s.u.
The charge on the inner sphere is 12e.s.u..
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Relation Between Electric Field And Potential
24 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A sphere of radius 0.03m is suspended within a hollow sphere of radius 0.05m. If the inner sphere is charged to a potential of 1500 volt and outer sphere is earthed. Find the capacitance and the charge of the inner sphere.
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere si earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the latter is much smaller ?
View Solution
Knowledge Check
A sphere of 10 cm diameter is suspended within a hollow sphere of 12 cm diameter. If the inner sphere be charged to a potential of 15,000 V and the outer sphere be earthed, the charge on the inner sphere is
A5×10−7CB6×10−7CC7×10−7CD8×10−7CA metal sphere of radius r is charged to certain potential V. Then the charge on the metal sphere
AIs more if its is hollowBIs more if its is solidCWill have same charge irrespective of being hollow or solidDCannot be charged if it is hollowA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
A400VB450VC500VD300V
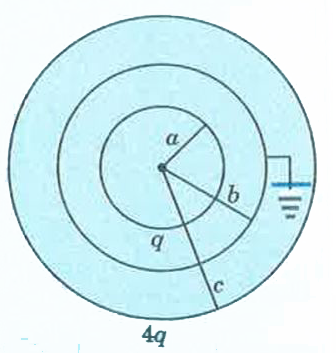
There are three concentric metallic spherical shells of radius a, b and c respectively as shown in the figure. The innermost sphere is given a charge q and the outermost sphere is given a charge 4q while the middle sphere is earthed. Find the charges appearing on the inner and outer surfaces of middle sphere.
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10 V. What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 5 cms is charged such that the potential on its surface is 10 volts. The potential at the centre of the sphere is
View SolutionA hollow metal sphere of radius 5cm is charged such that the potential on its surcace is 10V. The potential at the centre of the centre of the sphere is -
View Solution
