A point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
qε0
qπε0
q4ε0
q6ε0
The correct Answer is:D
To find the electric flux through the square due to a point charge q placed at a distance a2 directly above the center of the square, we can follow these steps:
1. Understanding the Configuration:
- We have a square of side a.
- The point charge q is located at a distance a2 above the center of the square.
2. Constructing a Gaussian Surface:
- To calculate the electric flux through the square, we can use Gauss's law. We will consider a cube (Gaussian surface) that has the square as one of its faces. The cube will have a side length of a.
3. Applying Gauss's Law:
- According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
- Here, qenc is the charge enclosed by the Gaussian surface, which in this case is q.
4. Calculating Total Flux:
- Since the charge is at the center of the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
5. Symmetry Consideration:
- The cube has 6 faces, and due to symmetry, the electric flux will be equally distributed among all the faces. Therefore, the flux through each face of the cube is:
Φface=Φtotal6=q6ϵ0
6. Identifying the Square Face:
- Since the square is one of the faces of the cube, the electric flux through the square is:
Φsquare=q6ϵ0
Final Answer:
The electric flux through the square is:
Φsquare=q6ϵ0
- We have a square of side a.
- The point charge q is located at a distance a2 above the center of the square.
- To calculate the electric flux through the square, we can use Gauss's law. We will consider a cube (Gaussian surface) that has the square as one of its faces. The cube will have a side length of a.
- According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
- Here, qenc is the charge enclosed by the Gaussian surface, which in this case is q.
- Since the charge is at the center of the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
- The cube has 6 faces, and due to symmetry, the electric flux will be equally distributed among all the faces. Therefore, the flux through each face of the cube is:
Φface=Φtotal6=q6ϵ0
- Since the square is one of the faces of the cube, the electric flux through the square is:
Φsquare=q6ϵ0
The electric flux through the square is:
Φsquare=q6ϵ0
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Problems Based On Mixed Concepts
40 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion
37 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm. The magnitude of the flux through the square is
View Solution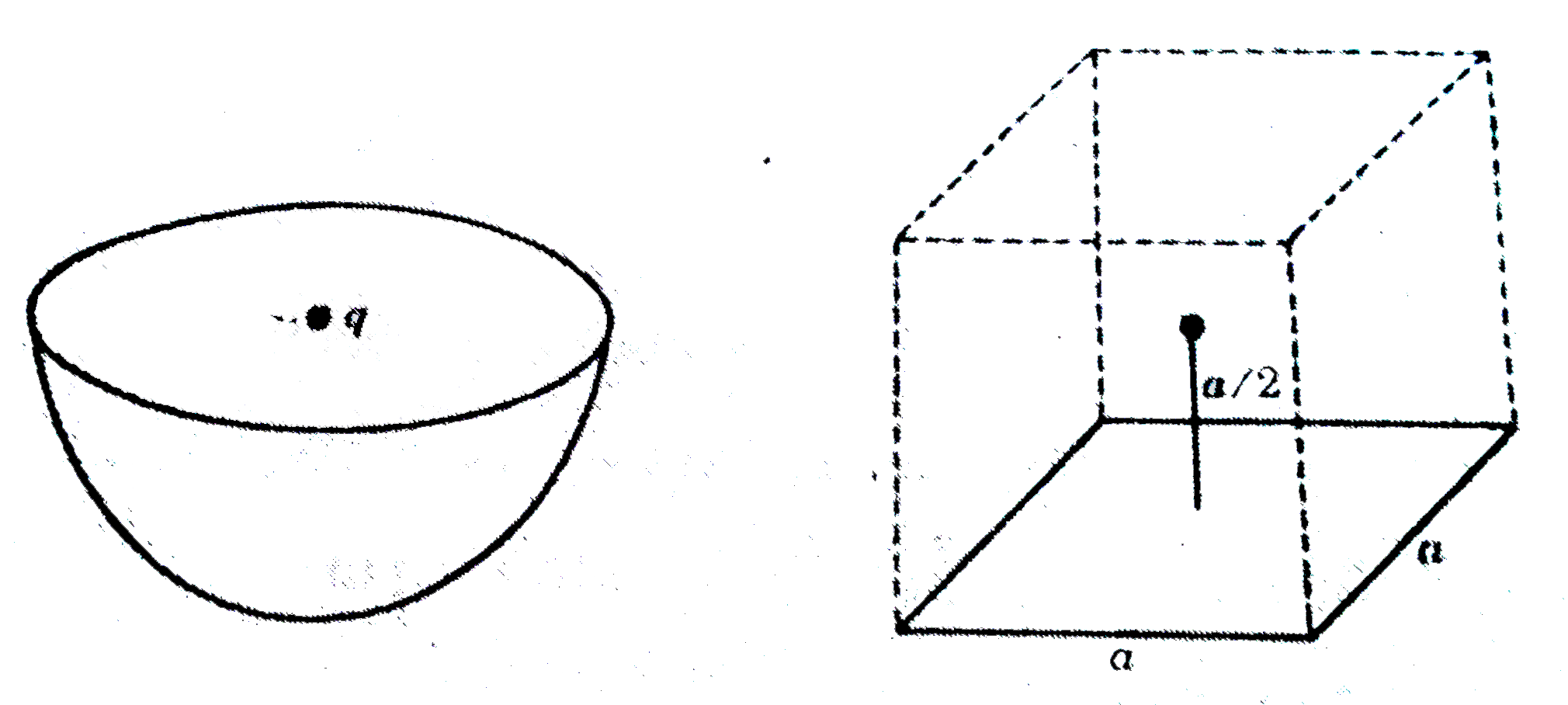
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
View Solution
Knowledge Check
A point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
Aqε0Bqπε0Cq4ε0Dq6ε0A point charge q is placed at a distance a2 directly above the centre of a horizontal square of side 'a' and another point charge -q is placed at a distance 'a' directly below one of its (the square's) corners. The electric flux through the square is :
Aq6∈0Bq8∈0Cq24∈0D5q24∈0A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
Aε0B1ε0Cε0×10−6D1ε0×10−6
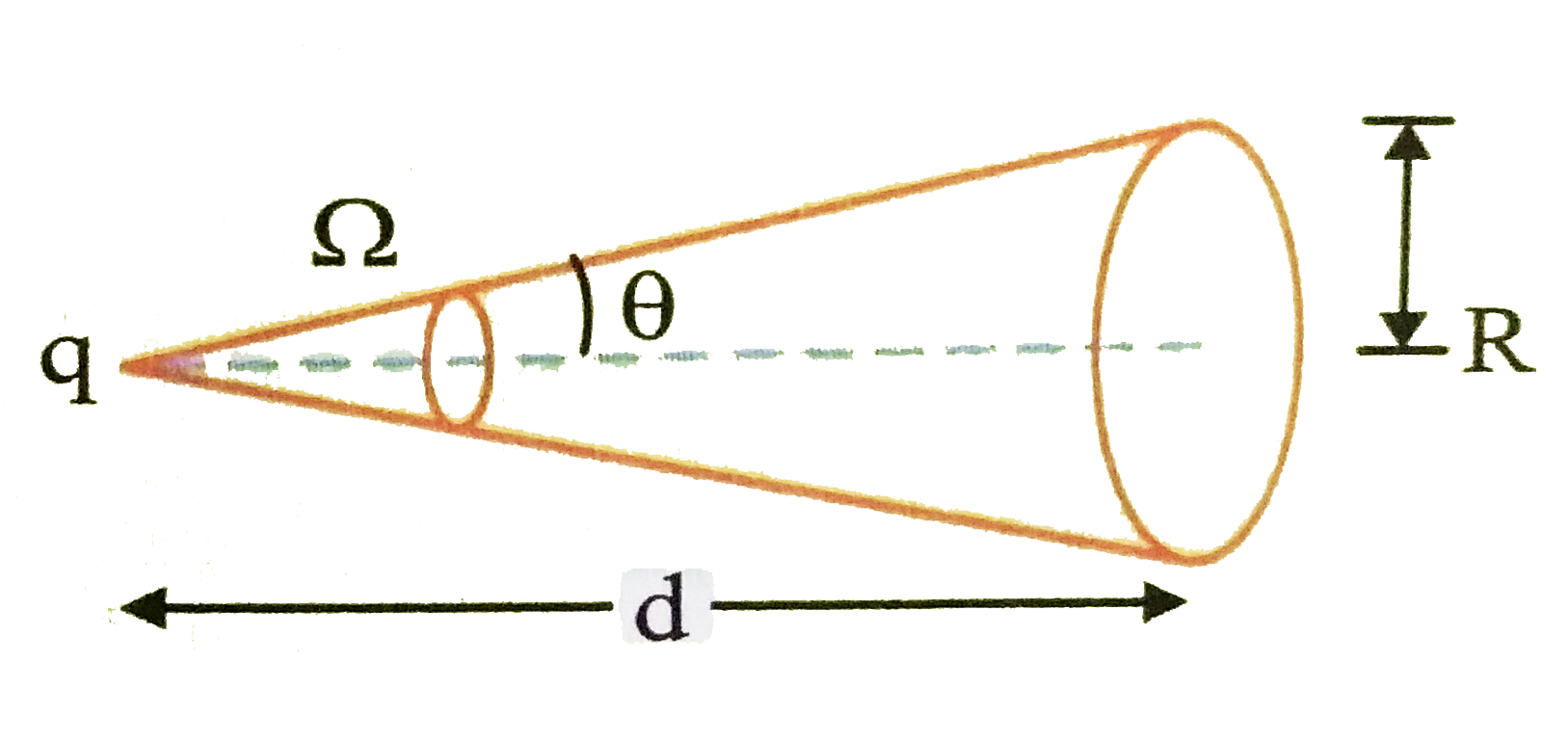
A point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
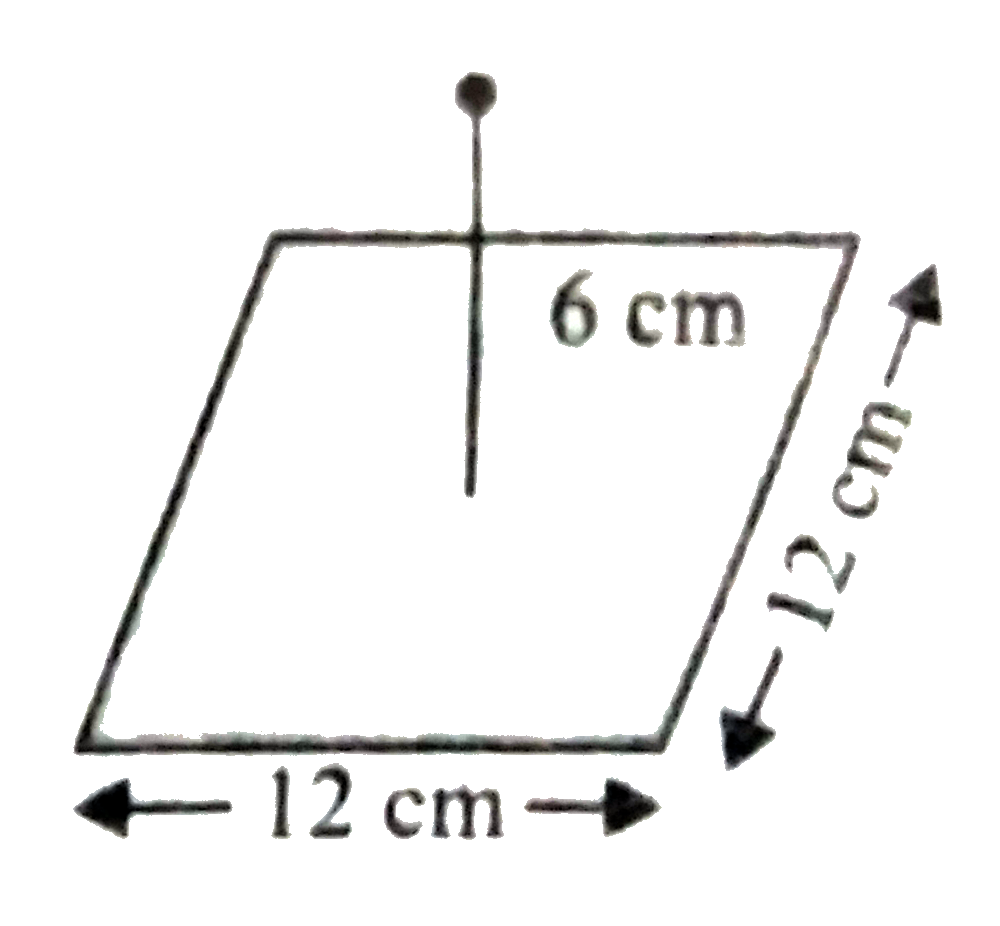
View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
View Solution(a) Define electric flux. Is is the scalar or a vector quantity?
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss's law to obtain the expression for the electric flux through the square.
(b) If the point charges is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.

View SolutionDefine electric flux, Is it a scalar or a vector quantity? A point charg q is at a distance of d2 directly above the centre of a square of side 'd' Use Gauss' law to obtain the expression for the electric flux through the square.
(b) If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled , explain how the electric flux will be affected.
View SolutionA point charge Q is placed at the corner of a square of side a, then find the flux through the square.

View Solution
