In ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
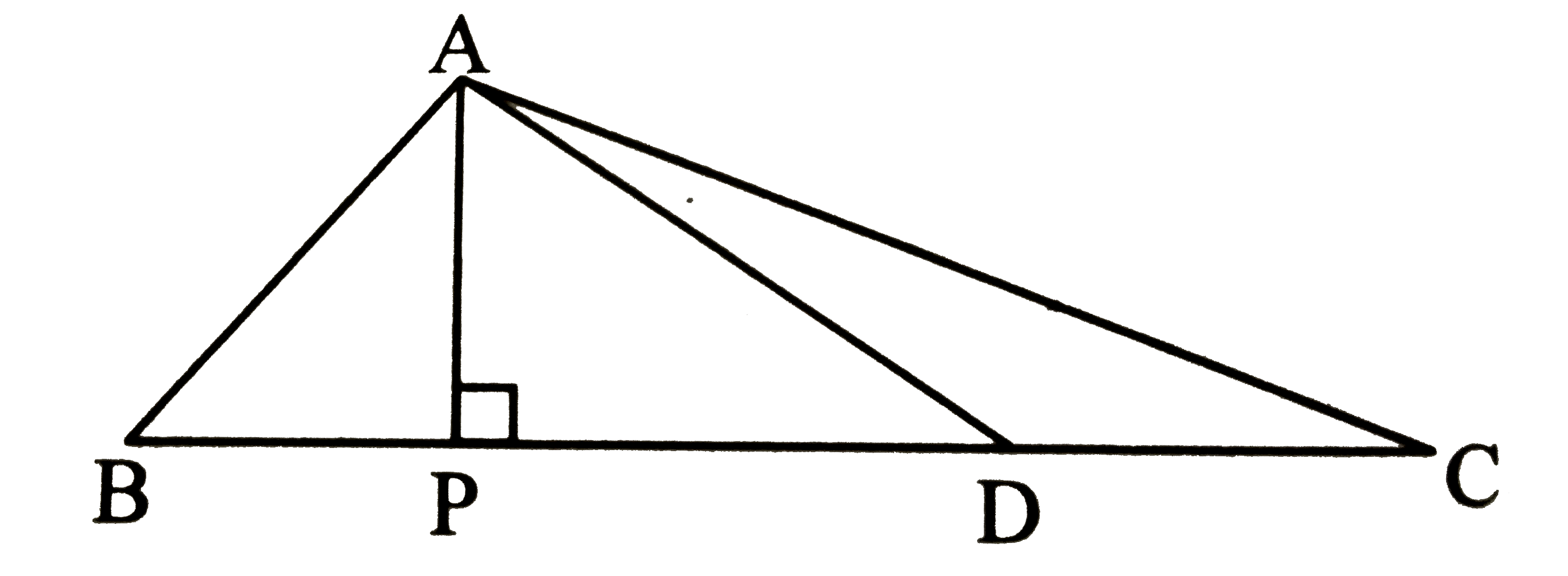
The correct Answer is:35 ii.32
Step by step video & image solution for In DeltaABC,point D is on side BC such that DC = 6, BC = 15. find (i)A(DeltaABD):A(DeltaABC) and (ii) A(DeltaABD):A(DeltaADC). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Additonal Problems for Practice(Based on Practice Set 1.2)
11 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Additonal Problems for Practice(Based on Practice Set 1.3)
7 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Multiple Choice Questions
28 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
In ΔABC,B - D - C and BD = 7, BC = 20, then find the ratio
A(ΔABD)A(ΔABC)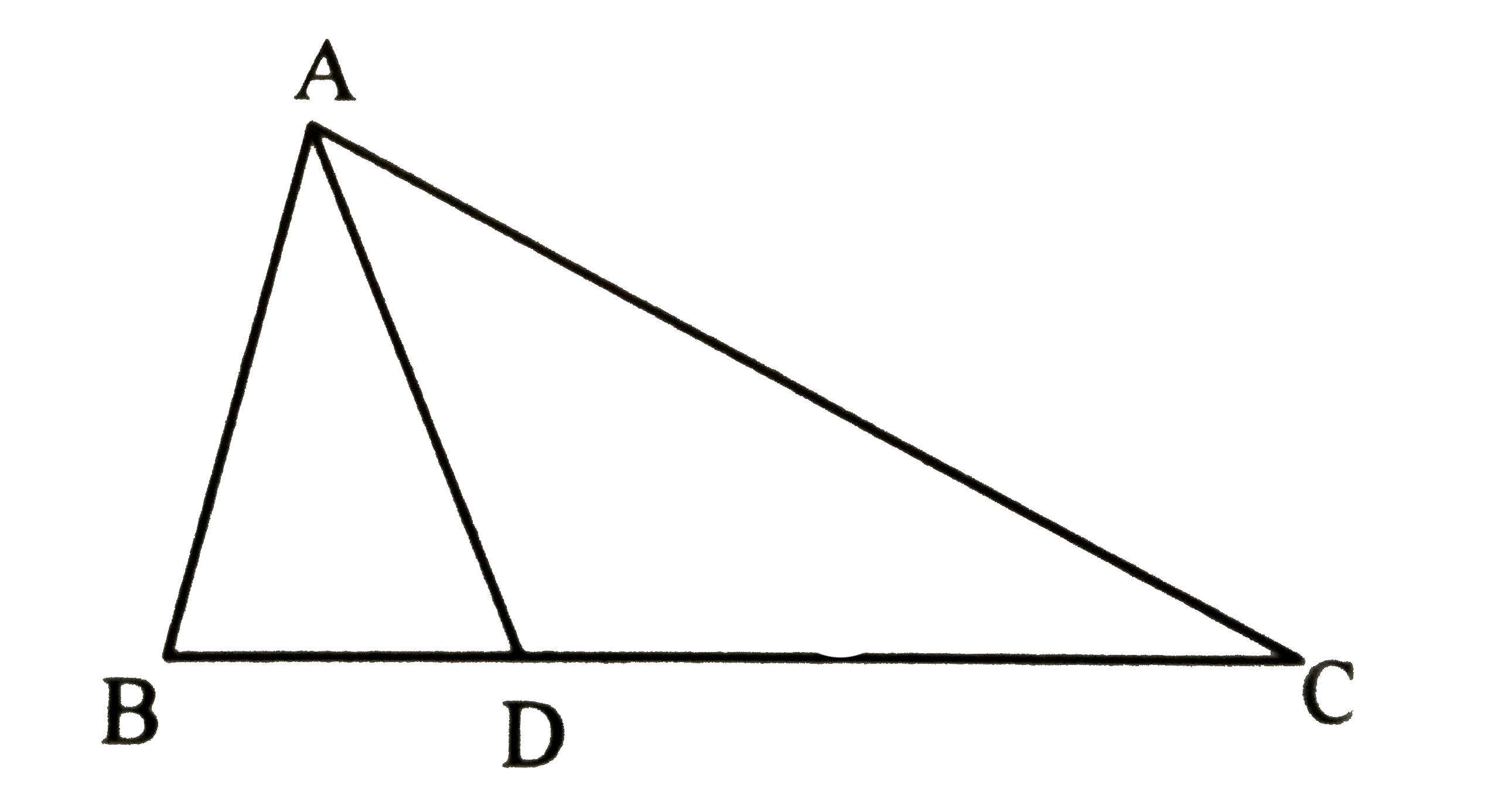
View SolutionIn ΔABC,B - D - C and BD = 7, BC = 20, then find the ratio.
A(ΔABD)A(ΔADC)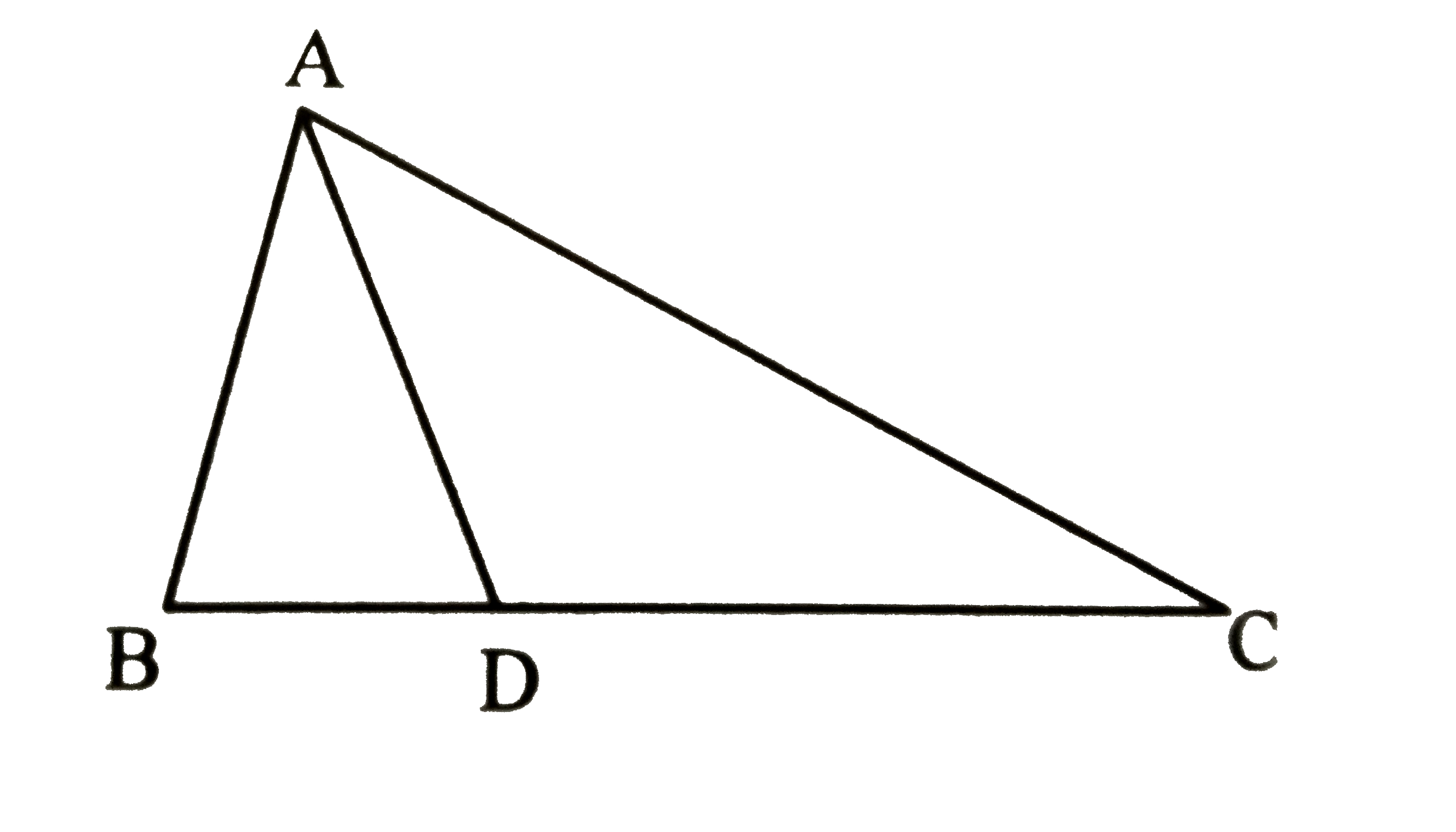
View SolutionIn ΔABC,AB+BC>
View SolutionIn the given figure, in ΔABC, point D is on side AC. If AC = 16, DC = 9 and BP⊥ AC then, find the following rations.
i. A(ΔABD)A(ΔABC)
ii.A(ΔBDC)A(ΔABC)
iii. A(ΔABD)A(ΔBDC)
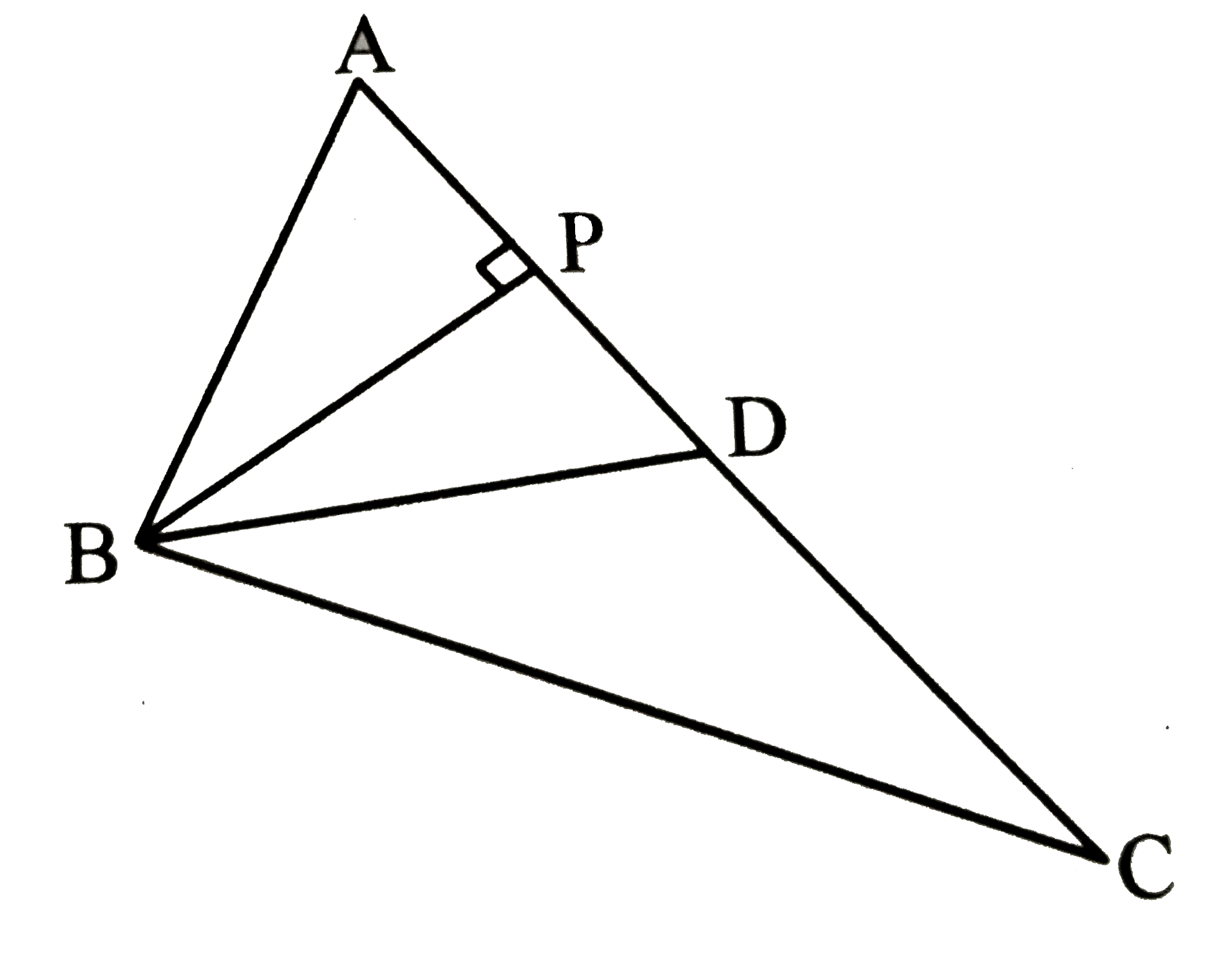
View SolutionIn ΔABC,B - D - C and BD = 7, BC = 20, then find following rations.
A(ΔADC)A(ΔABC)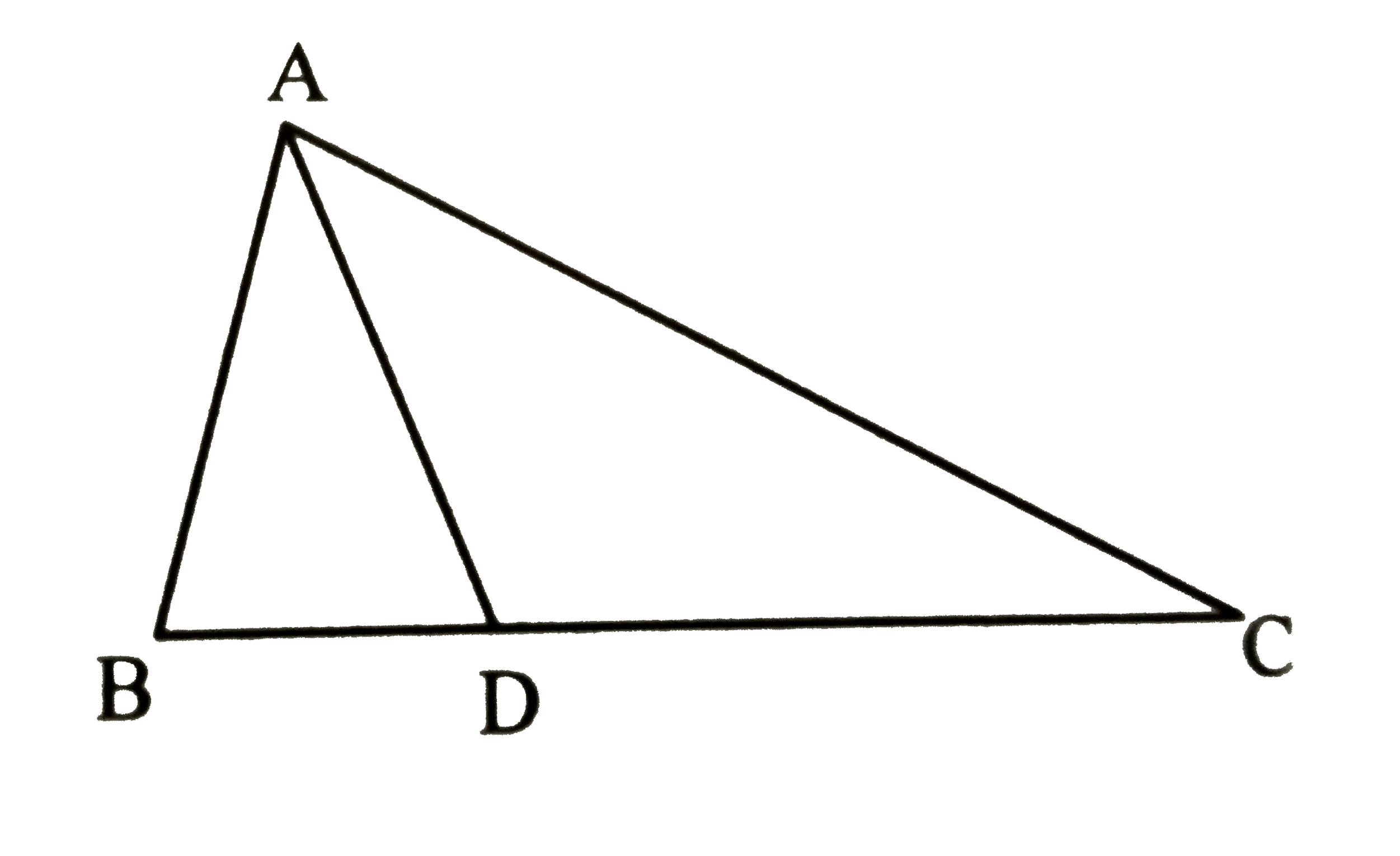
View SolutionIn ΔABC,B−D−C and BD=7,BC=20, then find followig ratios:

A(ΔABD)A(ΔADC)
A(ΔABD)A(ΔABC)
A(ΔADC)A(ΔABC)
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionIn the adjoining figure PQ⊥BC,AD⊥BC, then find following ratios:
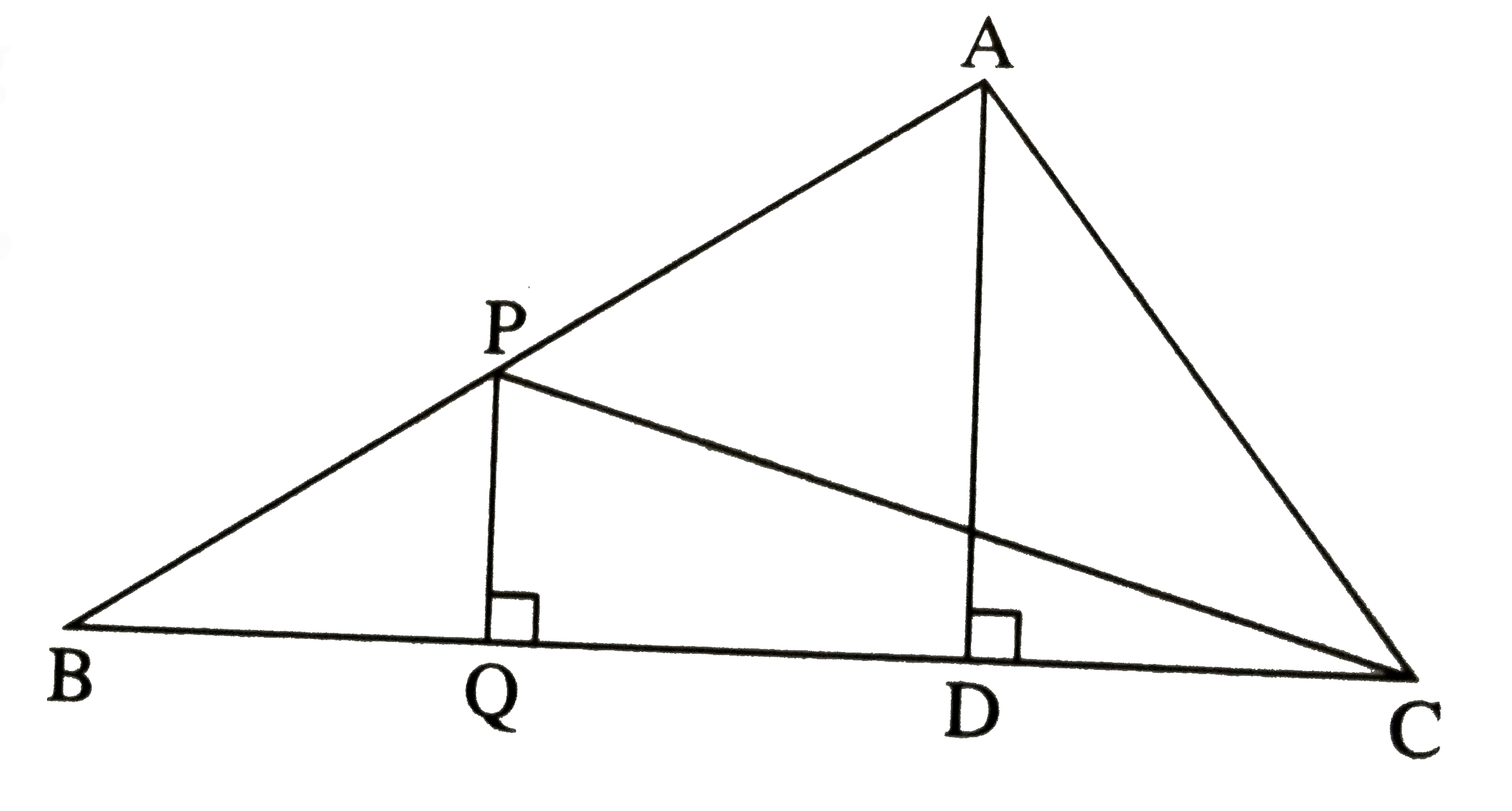
(i( A(ΔPQB)A(ΔPBC) (ii) A(ΔPBC)A(ΔABC)
(iii) A(ΔABC)A(ΔADC)(iv) A(ΔADC)A(ΔPQC)
View Solution
