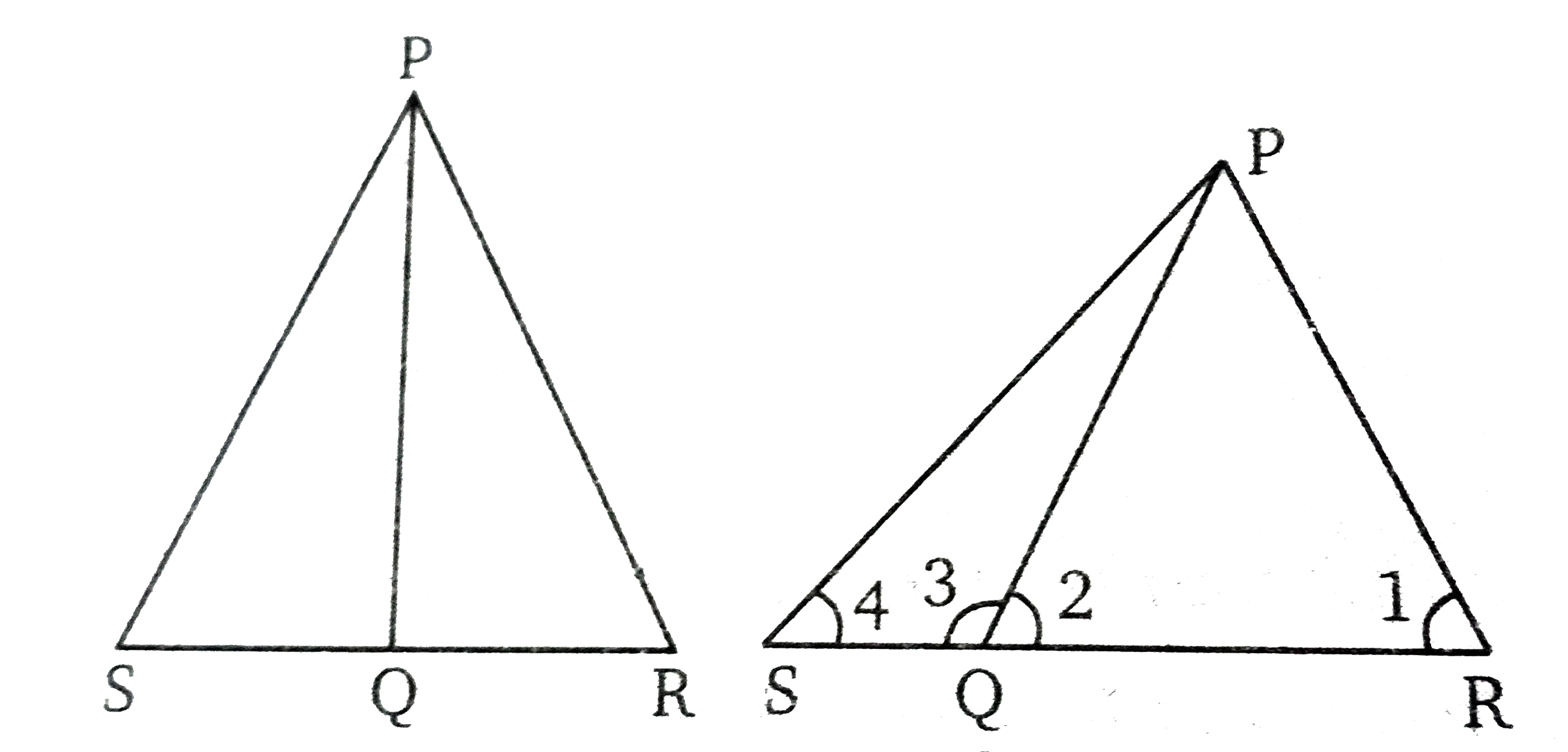
PC=PR तो सिध्द करो कि PS>PQ
ΔPQRमें,
PQ=PR [दिया है]
⇒ ∠PRQ=∠PQR [∵ समान भुजाओं के सम्मुख कोण समान होते हैं] ...(i)
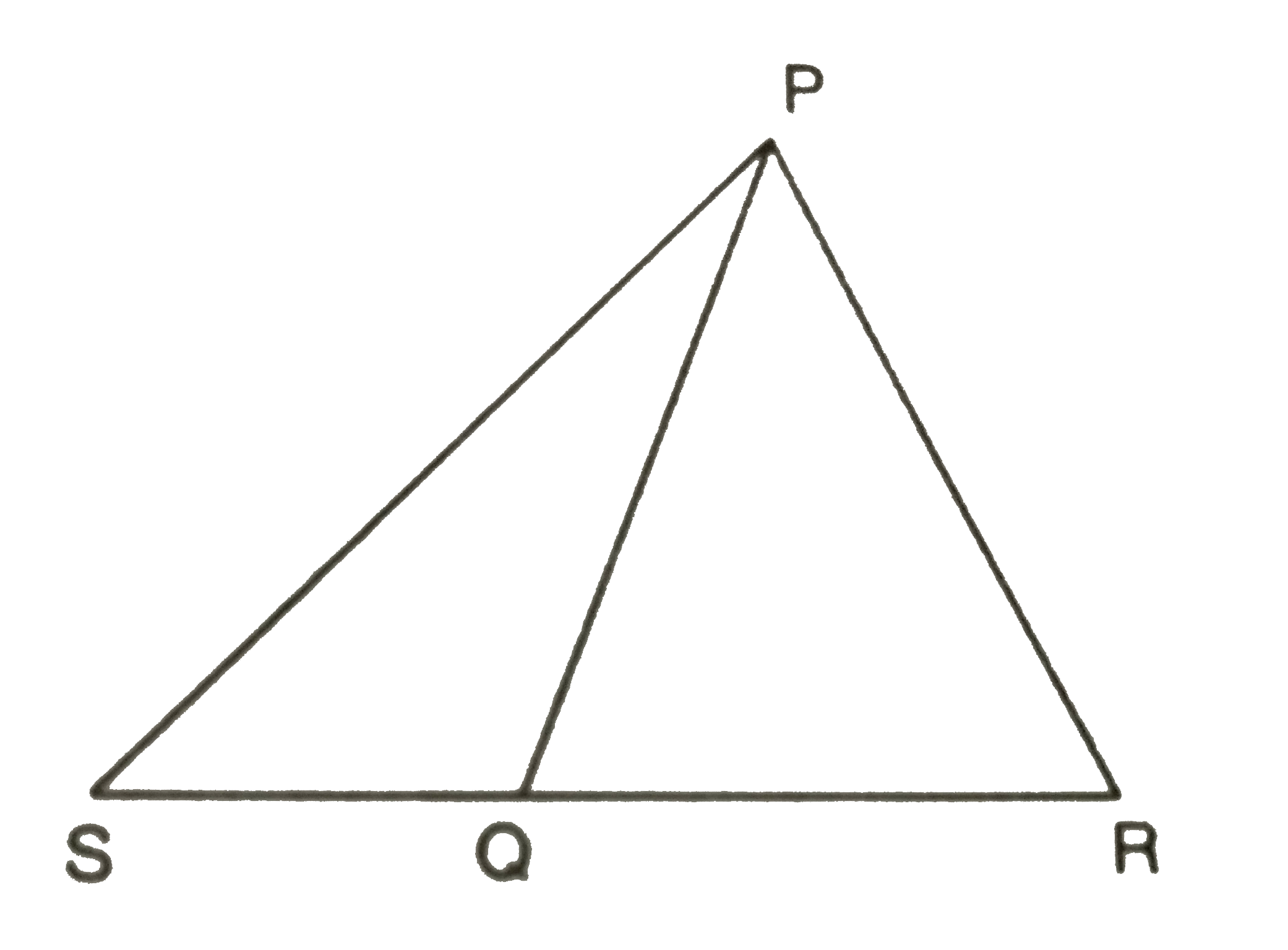
ΔPSQमें, SQ को R तक बढ़ाया है |
∴ बहिष्कोण∠PQR>∠PSQ [∵ त्रिभुज का बहिष्कोंण अपने प्रत्येक सम्मुख अन्तः कोणों से बड़ा होते है |] ...(ii)
(i)तथा (ii)से,
∠PRQ>∠PSQ
⇒ ∠PRS>∠PSR [:'∠PRQ=∠PRSतथा∠PSQ=∠PSR]
इसी प्रकार ΔPSRमें,
∠PRS>∠PSR
⇒ PS>PR [∵ बड़े कोण के सामने की भुजा बड़ी होती है]
परन्तु PR=PQ [दिया है]
∴ PS>PC
Topper's Solved these Questions
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:प्रश्नावली 10.1
Explore 13 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:प्रश्नावली 10.2
Explore 3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:बहु विकल्पीय प्रश्न
Explore 20 Videos
- सांखि्यिकीय आँकड़ों का सारणीयनBook:RD SHARMAChapter:सांखि्यिकीय आँकड़ों का सारणीयनExercise:बहु विकल्पीय प्रश्न
Explore 10 Videos
Similar Questions
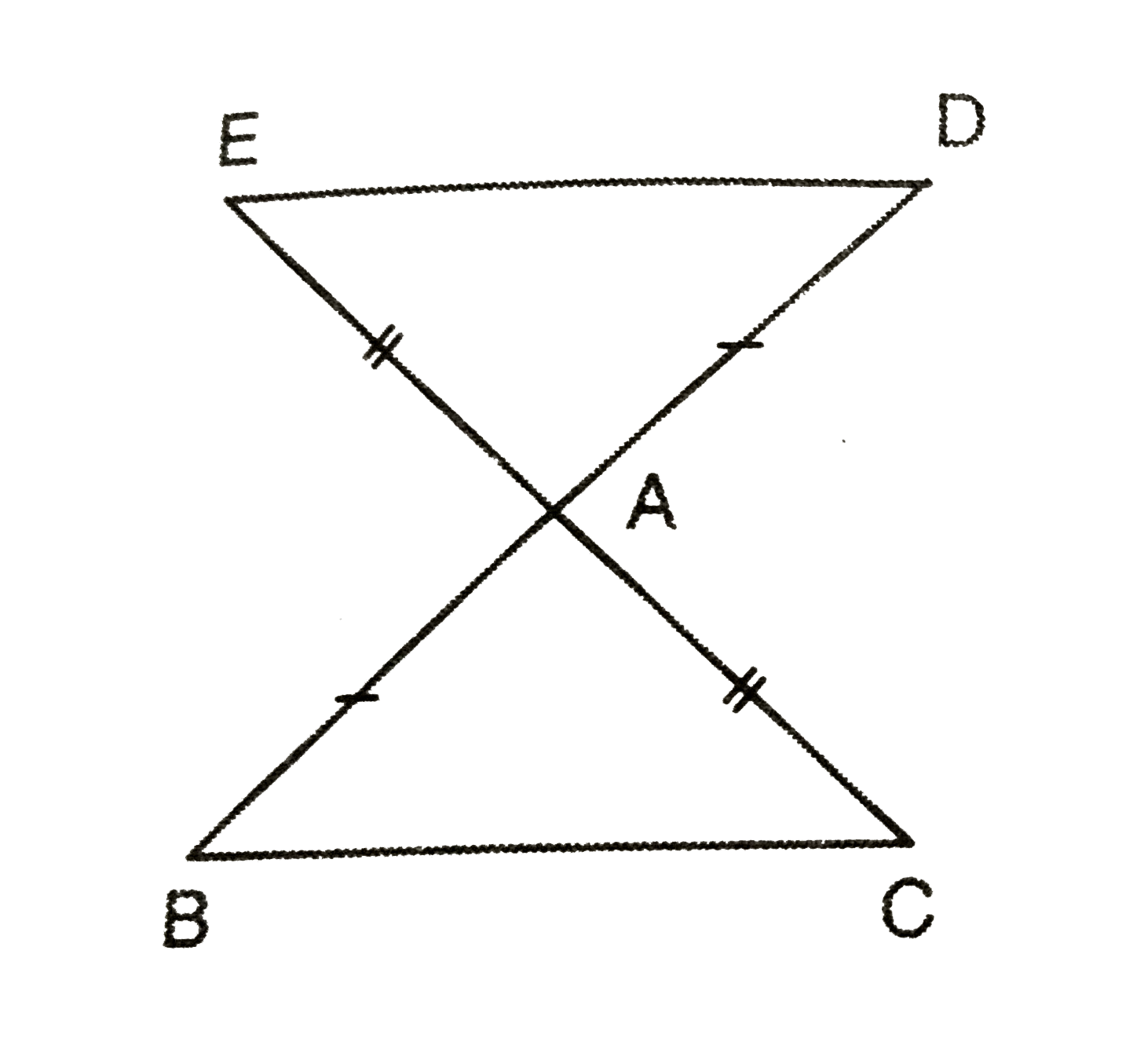
भुजाएँ BA तथा CA तथा इस प्रकार बढ़ाई गई कि BA=AD तथा CA=AE हैं | सिध्द कीजिए कि रेखाखण्ड DE∣∣BC है |
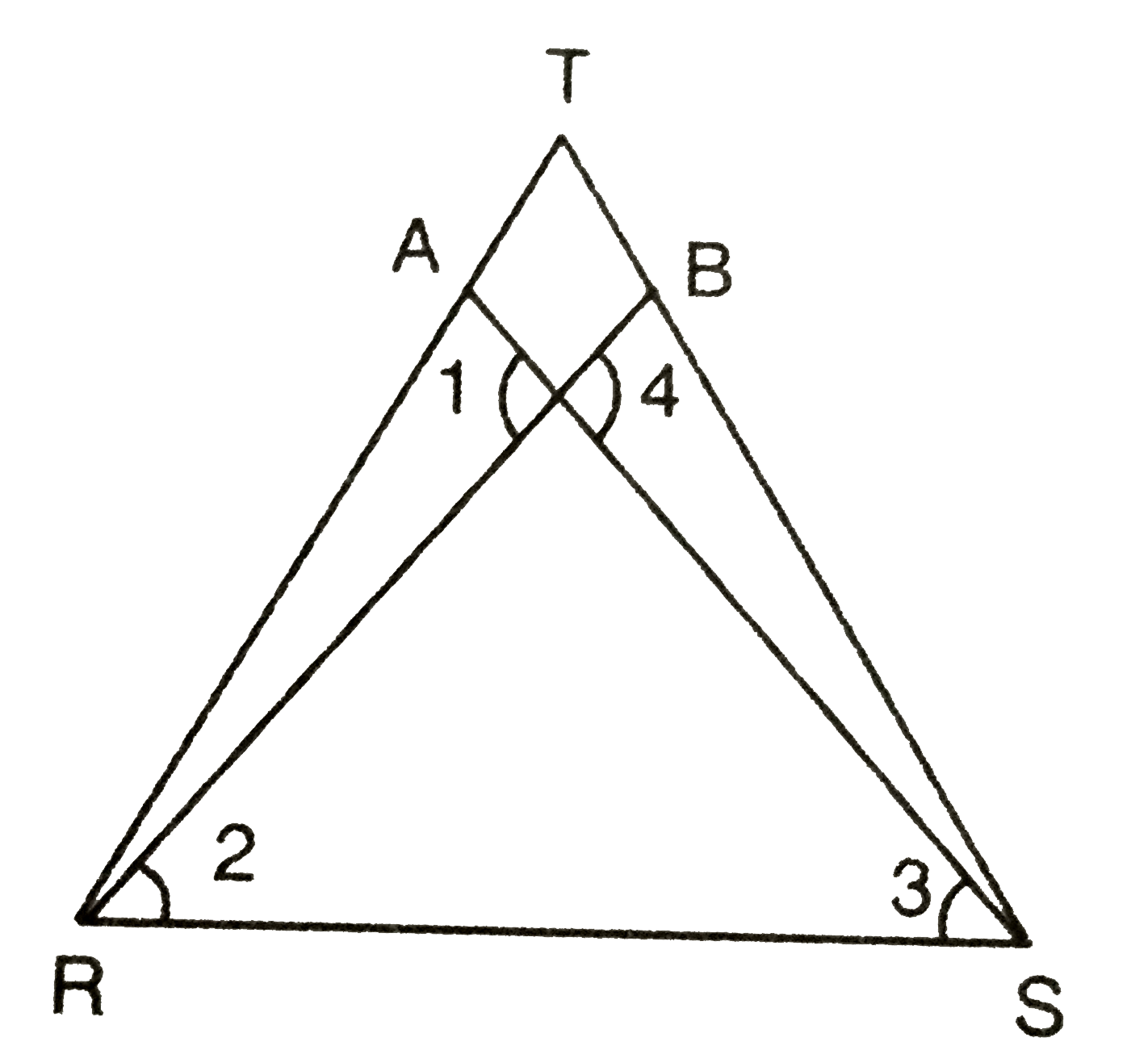
View Solutionयह दिया है RT=TS ∠1=2√3 तथा ∠4=2Sqrt(3)तो, दर्शाइए कि ΔRBT≅ΔSAT
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionप्रेक्षणो के सग्रह में से उच्चतम एव न्यूनतम प्रेक्षणो के अन्तर को कहते है ?
View SolutionIn Figure, PQ=PR . Show that PS>PQ
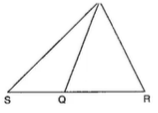
View SolutionIn Figure, PQ=PR. Show that PS>PQ
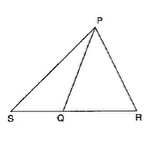
View SolutionIn the adjoining figure, PQ=PR. Show that PS>PQ.
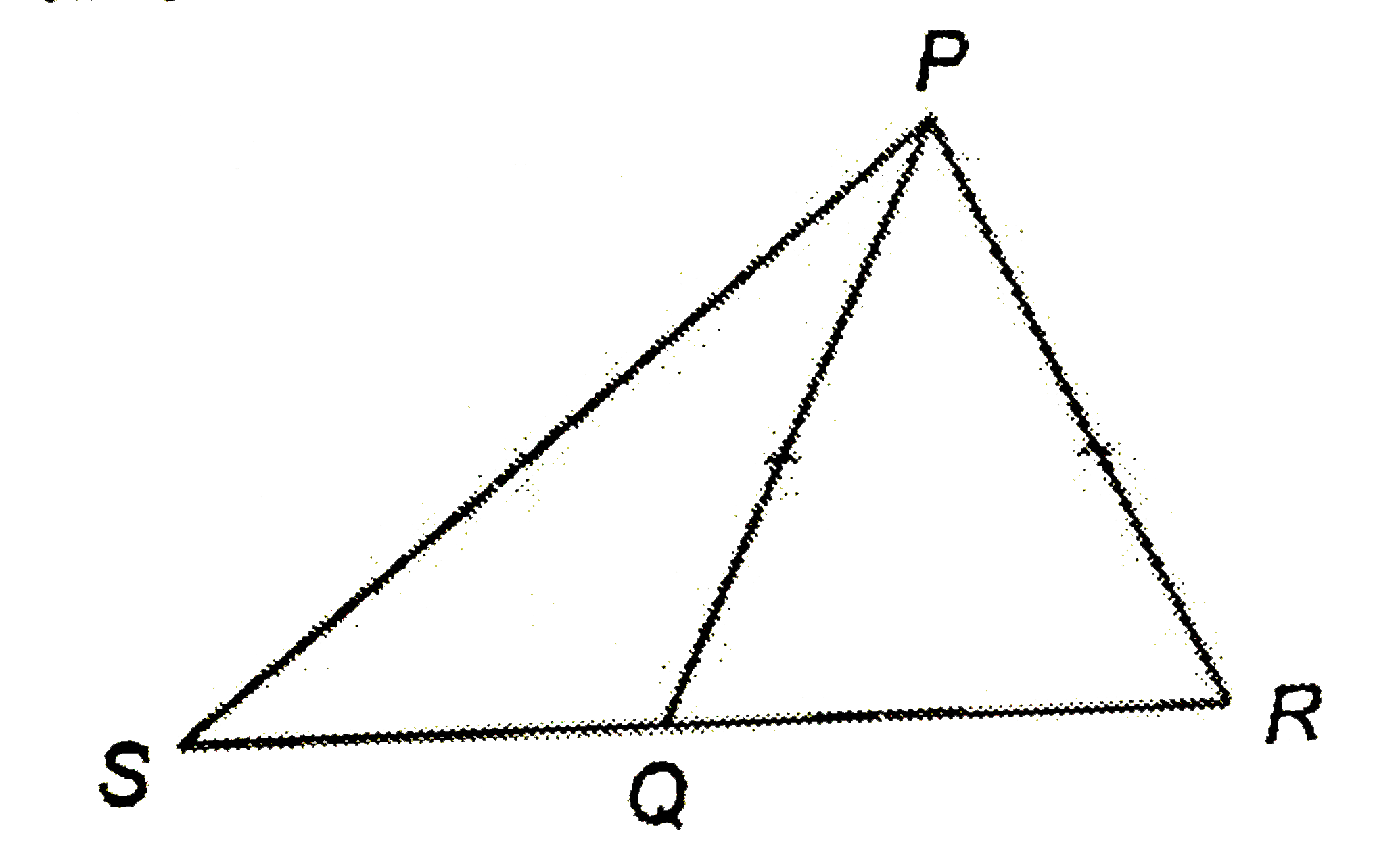
View SolutionIn the given figure, AP⊥QR,PR>PQandPQ=PS. Show that AR>AQ.

View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
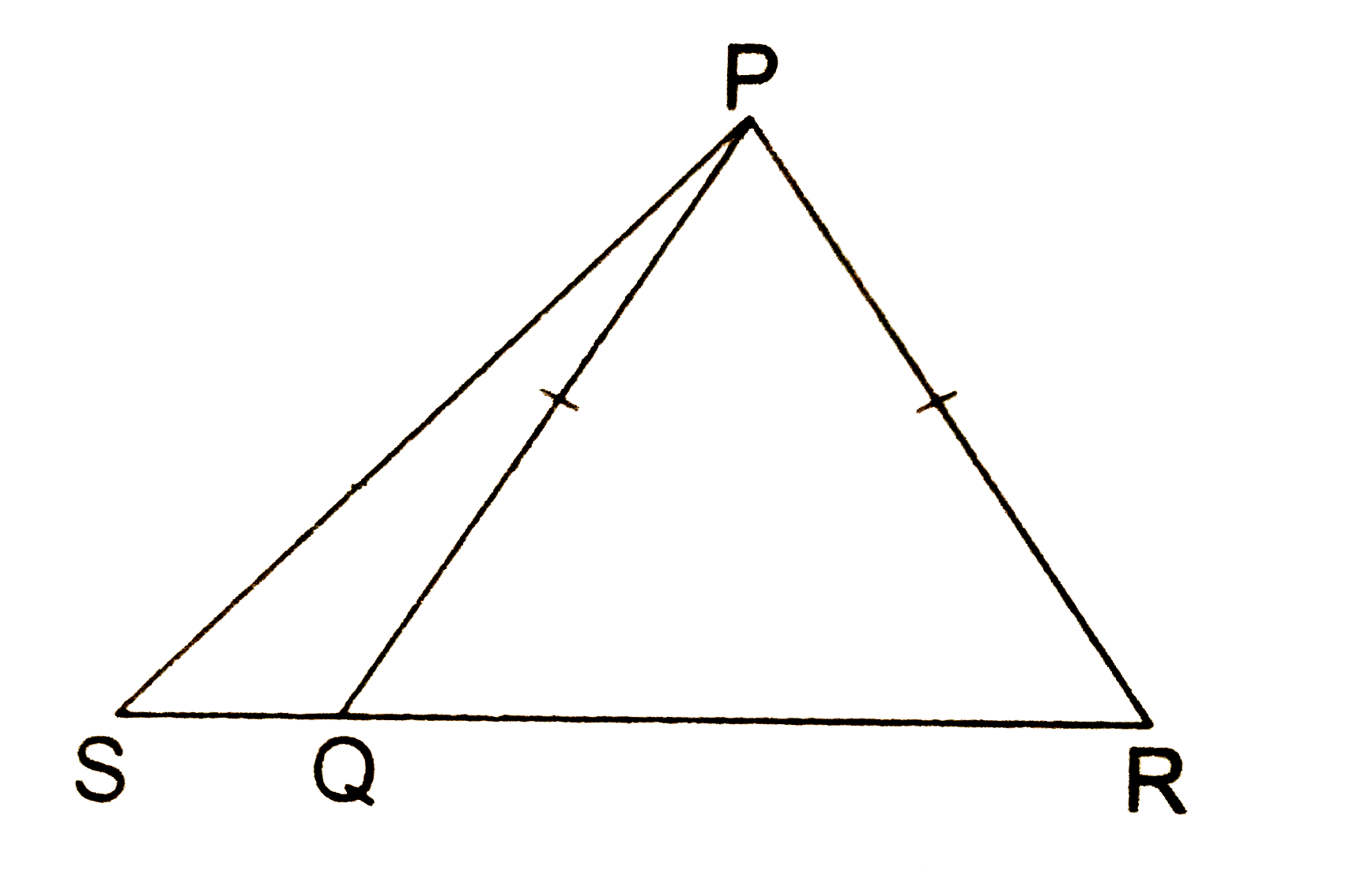
View Solutionआकृति में, PR>PQ है और PS, ∠QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR>∠PSQ है।

View Solutionदी गई आकृति में PR>PQ और PS, P का समद्विभाजक है | दिखायें कि x>y.
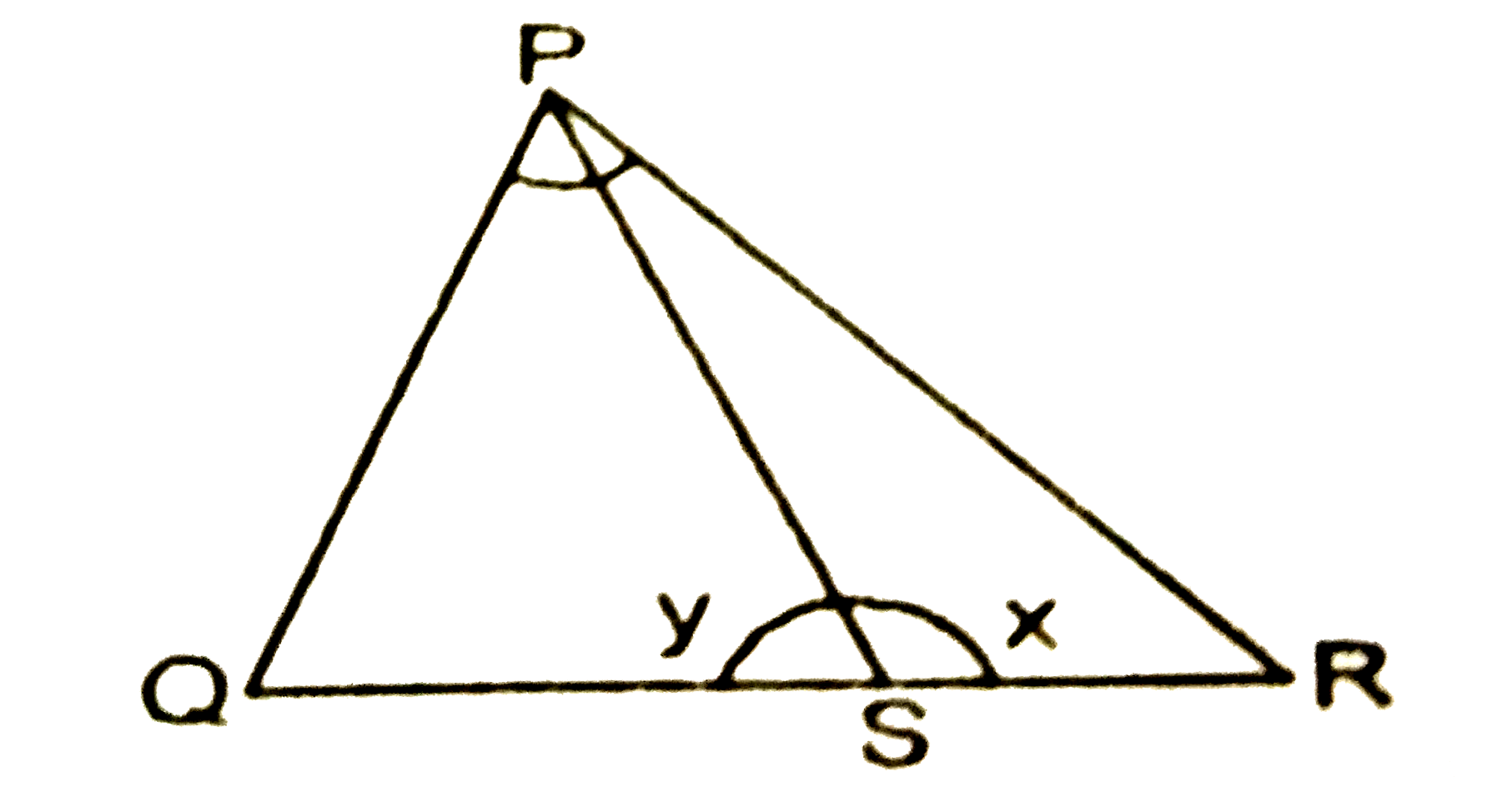
View Solutionदिये गये चित्र में , ΔPSR की भुजा SR पर एक बिंदु Q इस प्रकार है कि PQ = PR तो दिखाइये कि PS>PQ
View Solutionयदि चतुर्भुज PQRS कि भुजाओं PS तथा RS पर क्रमशः T तथा U इस प्रकार हैं कि PQ=RQ, anglePQT=angleRQUतथाangleTQS=angleUQS तो, सिध्द करो कि QT=QU.
View Solutionआकृति में PR = PQ तो सिद्ध करें की PS>PQ
View Solutionएक ΔPSR कि भुजा SR पर एक बिंदु Q इस प्रकार स्थित है की PQ = PR है। सिद्ध कीजिए की PS>PQ
View Solution

