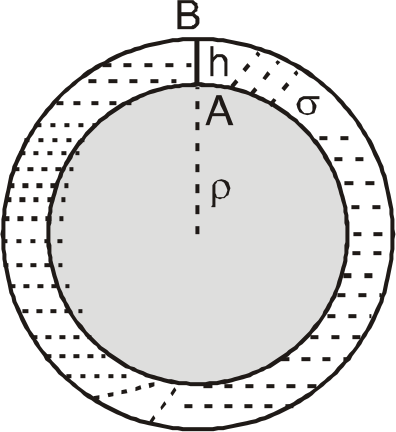
Suppose the earth was covered by an oceam of uniform depth h,(hltltR)

Suppose the earth was covered by an ocean of uniform depth $h, (h < < R)$ Let $σ$ be density of ocean and $p$ be mean density of earth. Let $Δ g$ be the approximate difference of value of net acceleration duet to gravity between the bottom of the ocean and top $(Δ g = g + (top) - g_{bottom})$ . Choose the correct option.
A $Δ g = \frac{4}{3} π G h [2 ρ - 3 σ]$
B $Δ g = \frac{4}{3} G π h [3 σ - 2 ρ]$
C $Δ g = \frac{4}{3} G π h [2 σ - 3 ρ]$
D $Δ g = \frac{4}{3} G π h [3 ρ - 3 σ]$
One end of a string of length $L$ is tied to the ceiling of a lift acceleration upwards with an acceleration $2 g$ . The other end of the string is free. The linear mass density of the string varies linearly from $0 \to λ$ from bottom to top. Choose the correct option(s)
AThe velocity of the wave in the string will be 0.
BThe acceleration (relative to string) of the wave on the string will be $3 g / 4$ every where.
CThe time taken by a pulse to reach from bottom to will be $\sqrt{8 L / 3 g}$ .
DThe time taken by a pulse to reach from bottom to top will be $\sqrt{4 L / 3 g}$ .
Let $g_{h}$ and $g_{d}$ the acceleration due to gravity at height h above the earth s surface and at depth d below the earth surface respecitively if $g_{h} = g_{d}$ then the releation between h and d is
A $d = h$
B $d = \frac{h}{2}$
C $d = \frac{h}{4}$
D $d = 2 h$

One end of a string of length $L$ is tied to the ceiling of a lift acceleration upwards with an acceleration $2 g$ . The other end of the string is free. The linear mass density of the string varies linearly from $0 \to λ$ from bottom to top. Choose the correct option(s)