Three projecties are thrown all with same speed u but at different angles of projection (θ>θ2>θ3) all taken from horizontal. Maximum height attained by projectile (3) is H. Range of (1) & (3) is same & that of (2) is maximum for the given speed. At height H, speeds are v1,v2&v3 as shown. Total time of flights are T1,T2&T3. Choose the correct statement(s).
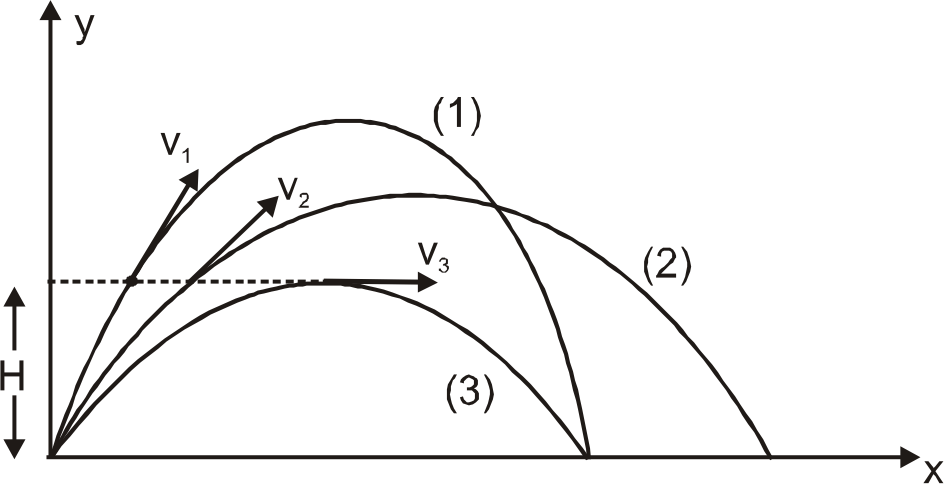
v1>v2>v3
v1=v2=v3
T21,T22&T23 are in AP
θ,θ2&θ3 are in AP
from work energy theorem
v1=v2=v3
θ1+θ2=90∘&θ2=45∘
⇒θ1+θ32=θ2⇒θ1,θ2&θ3 are in AP
T1=2usinθ1g⇒T2=2usin45∘g⇒T3=2ucosθ1g
⇒T21+T232=T22⇒T21,T22&T23 are in AP
Topper's Solved these Questions
Similar Questions
A particle is thrown with speed of 50m/s at an angle of projection 37∘ with the horizontal. Find (a) the time of flight, (b) the maximum height attained and ( c) the horizontal range.
(sin37∘=35,cos37∘=45)
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectily
View Solution
Knowledge Check
Two particles projected form the same point with same speed u at angles of projection αandβ strike the horizontal ground at the same point. If h1andh2 are the maximum heights attained by the projectile, R is the range for both and t1andt2 are their times of flights, respectively, then
Aα+β=π2BR=4(√h1h2)Ct1t2=tanαDtanα=(√h1h2)A body is thrown up with a speed u, at an angle of projection θ If the speed of the projectile becomes u√2 on reaching the maximum height , then the maximum vertical height attained by the projectile is
Au24gBu23gCu22gDu2gTwo stones are thrown with same speed u at different angles from ground n air if both stones have same range and height attained by them are h1andh2, then h1+h2 is equal to
Au2gBu22gCu23gDu24g
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in the two cases:-
View SolutionA projectile has the same range R for two angles of projections but same speed. If T1 and T2 be the times of flight in the two cases, then
Here θ is the angle of projection corresponding to T1.
View SolutionTwo balls are thrown with the same speed from a point O at the same time so that their horizontal ranges are same. If the difference of the maximum height attained by them is equal to half of the sum of the maximum heights, then the angles of projection for the balls are
View SolutionTwo stones are projected with the same speed but making different angles with the horizontal. Their horizontal ranges are equal. The angle of projection of one is π3 and the maximum height reached by it is 102 m. Then the maximum height reached by the other in metres is
View SolutionA projectile thrown with an initial speed u and the angle of projection 15∘ to the horizontal has a range R. If the same projectile is thrown at an angle of 45∘ to the horizontal with speed 2u, what will be its range ?
View Solution

