Magnetic field is uniform and has a magnitude B in the interior of a very solenoid far from its ends. One of the ends of the solenoid is closed with a thin flat plastic cover. A single small electrical loop of radius R lies on the cover so that its center is on the axis of the solenoid. The electrical current flowing in the loop in I. If the mechanical tension in the loop's wire is BIRx, then the value of x :

B at end =12 B at interior =12 B
IdL(B2)=2Tsindθ
dL=R(2dθ)
IR.2dθB2=2Tdθ
T=BIR2

Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
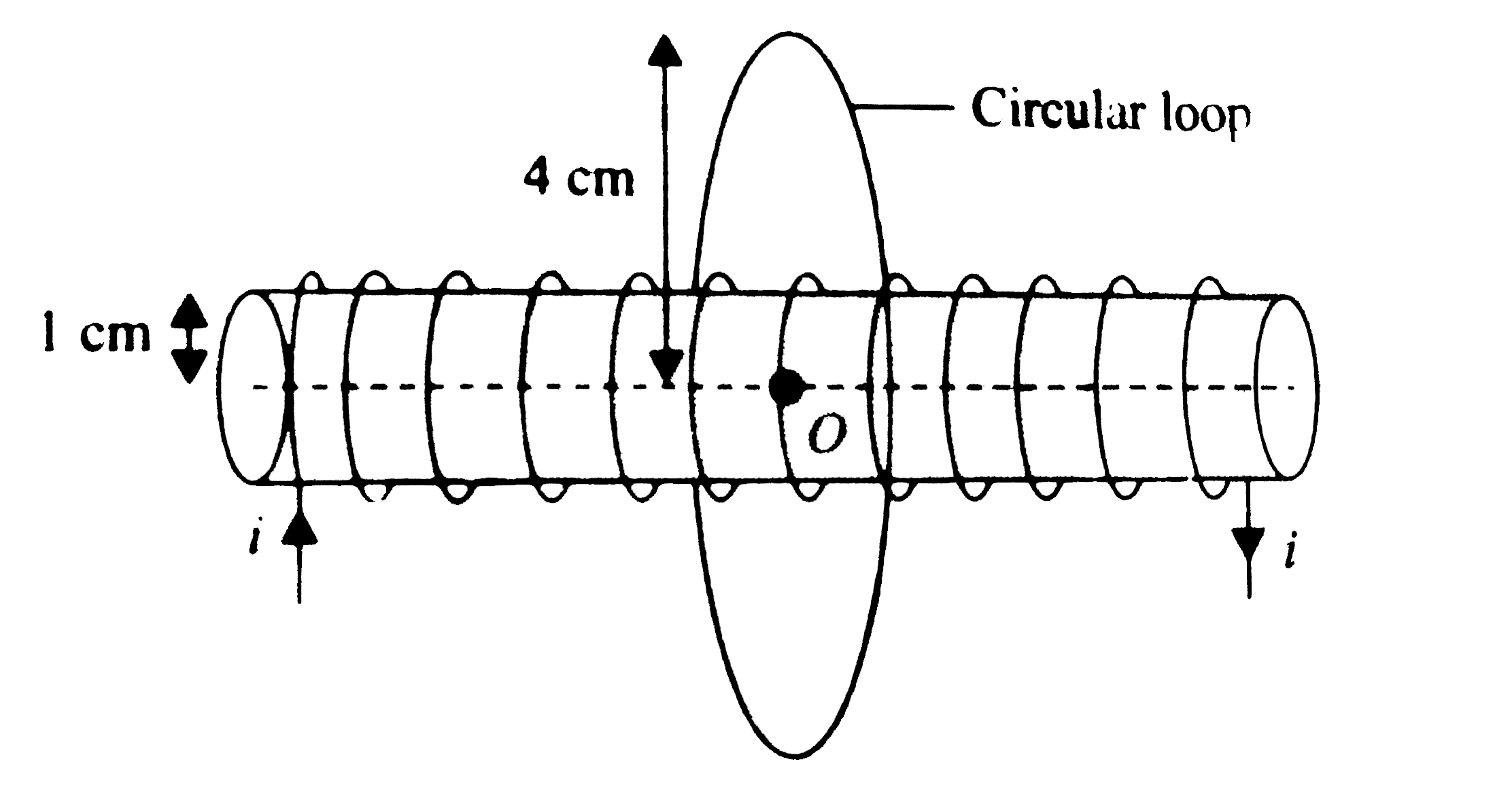
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionAssertion : The magnetic filed at the ends of a very long current carrying solenoid is half of that at the center. Reason : If the solenoid is sufficiently long, the field within it is uniform.
View SolutionA long solenoid has 800 turns per metre length of solenoid A current of 1.6 A flow through it. The magnetic induction at the end of the solenoid on its axis is
View Solutionएक परिनालिका I में विद्युत प्रवाहित होने के उपरान्त चुम्बकीय क्षेत्र B है |परिनालिका की लम्बाई व फेरो की संख्या को दुगुना करने की पर चुम्बकीय क्षेत्र प्राप्त करने के लिए प्रवाहित धारा करनी पड़ेगी -
View SolutionMagnetic Field Due To Current Carrying Loop | Solenoid
View SolutionAssertion: Intensity of magnetic field due to a solenoid near its ends is only half of its magnitude inside the solenoid.
Reason: If solenoid is made very long then magnetic field inside the solenoid becomes uniform.
View Solution(A) : The magnetic field at the ends of a very long current carrying solenoid is half of that at the centre.
(R) : If the solenoid is sufficiently long, the field within it is uniform.
View Solution(A) : Solenoid produces uniform magnetic field along its axis.
(R) : Field of a solenoid is independent of its radius.
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionA long solenoid has 800 turns per metre length of solenoid A currentof 1.6 A flow through it. The magnetic induction at the end of the solenoid on its axis is
View Solution