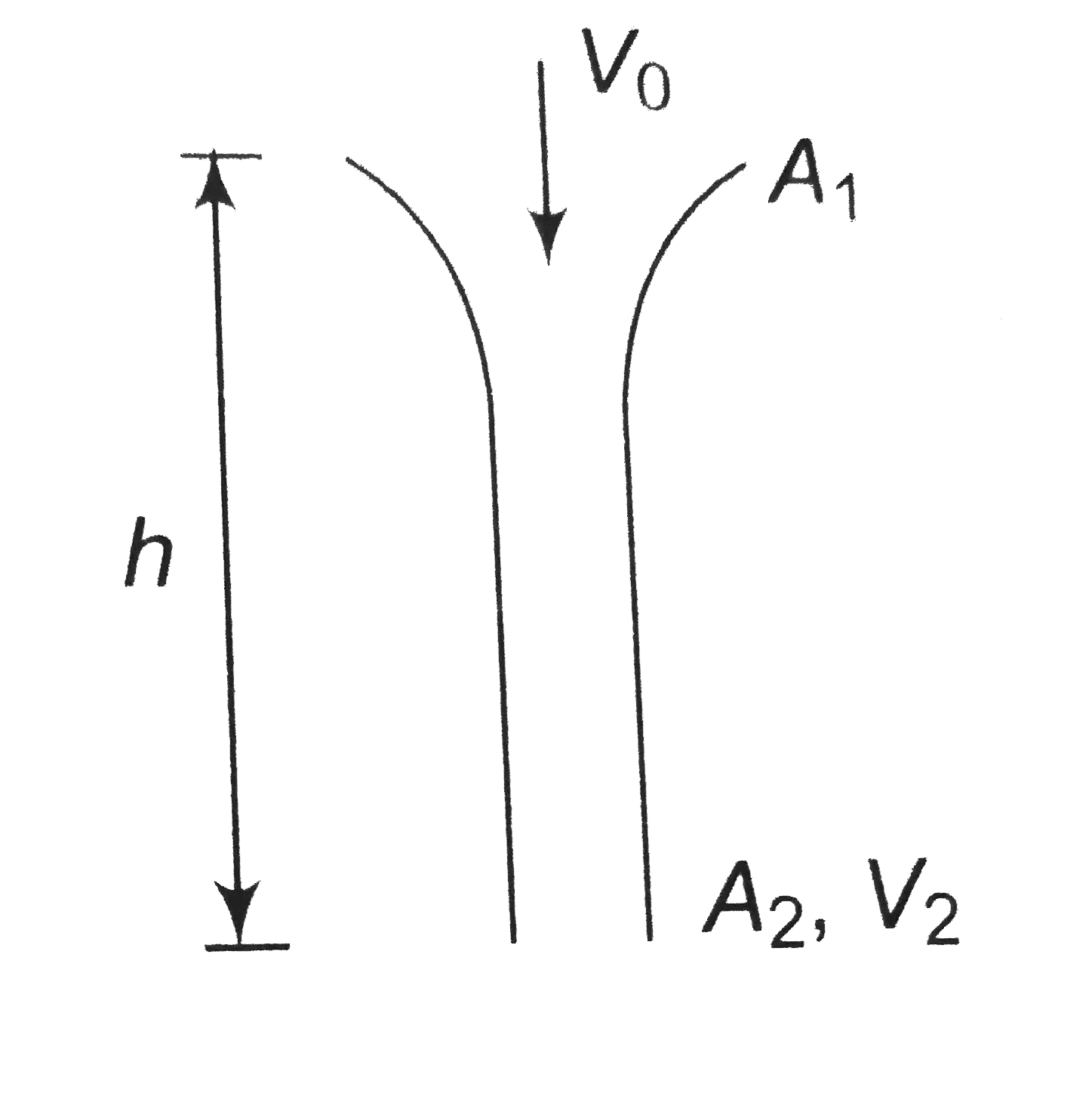
Water from a tap emerges vertically downwards with an initial velocity V0. Assume pressure is constant throughout the stream of water and the flow is steady. Find the distance form the tap at which cross-sectional area of stream is half of the cross-sectional area of stream at the tap.
V20/2g
3V20/2g
2V20/2g
5V20/2g
The correct Answer is:B
V22=V20+2gh
and A1V0=A2V2
Solving ,A2A1=V0√V20+2gh
A2/A1=12=V0√V20+2gh
4V20=V20+2gh
h=3V202g.
Topper's Solved these Questions
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Application Of Bernoulli'S Theorem And Velocity Of Efflux
Explore 19 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Problems Based On Mixed Concepts
Explore 29 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Buoyancy And Floatation
Explore 40 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
Water from a tap emerges vertically downwards an intial speed of 1 m/s . The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is contant throughout the stream of water and that the flow is steady . The cross-sectional area of the steam. 0.15 m below the tap is
View SolutionWater from a tap emerges vertically downward with an initial speed of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the flow is steady. What is the cross-sectional area of the stream 0.15 m below the tap? Use g=10ms−2.
View Solution
Knowledge Check
Water from a tap emerges vertically downwards with an initial spped of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
A(a) 5.5×10−4m2B(b) 1.0×10−5m2C(c) 5.0xx10^-5m^2D(d) 2.0xx10^-5m^2Water from a tap emerges vertically downward with an initial speed of 3.0 m/s. The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is constant throughout the stream of water and that the flow is steady. The cross-sectional area of the stream 2 m below the tap is:
A0.7×10−5m2B10−4m2C4.3×10−5m2D2.8×10−5m2Water from a tap emerges vertically downwards with iitial velocity 4ms−1. The cross-sectional area of the tap is A. The flow is steady and pressure is constant thorughout the stream of water. The distance h vertically below the tap, where the cross-sectional area of the stream becomes (23)A is (g=10m/s2)
A0.5 mB1 mC1.5 mD2.2 m
The water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionA laminar stream is flowing vertically down from a tap of cross-section area 1cm2. At a distance 10 below the tap, the cross-section area of the stream has reduced to 1/2cm2. Find the volumetric flow rate of water from the tap.
View SolutionIn the previous question, at the mouth of the tap the area of cross-section is 2.5cm2 and the speed of water in 3m/s. The area of cross-section of the water column 80cm below the tap is.
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
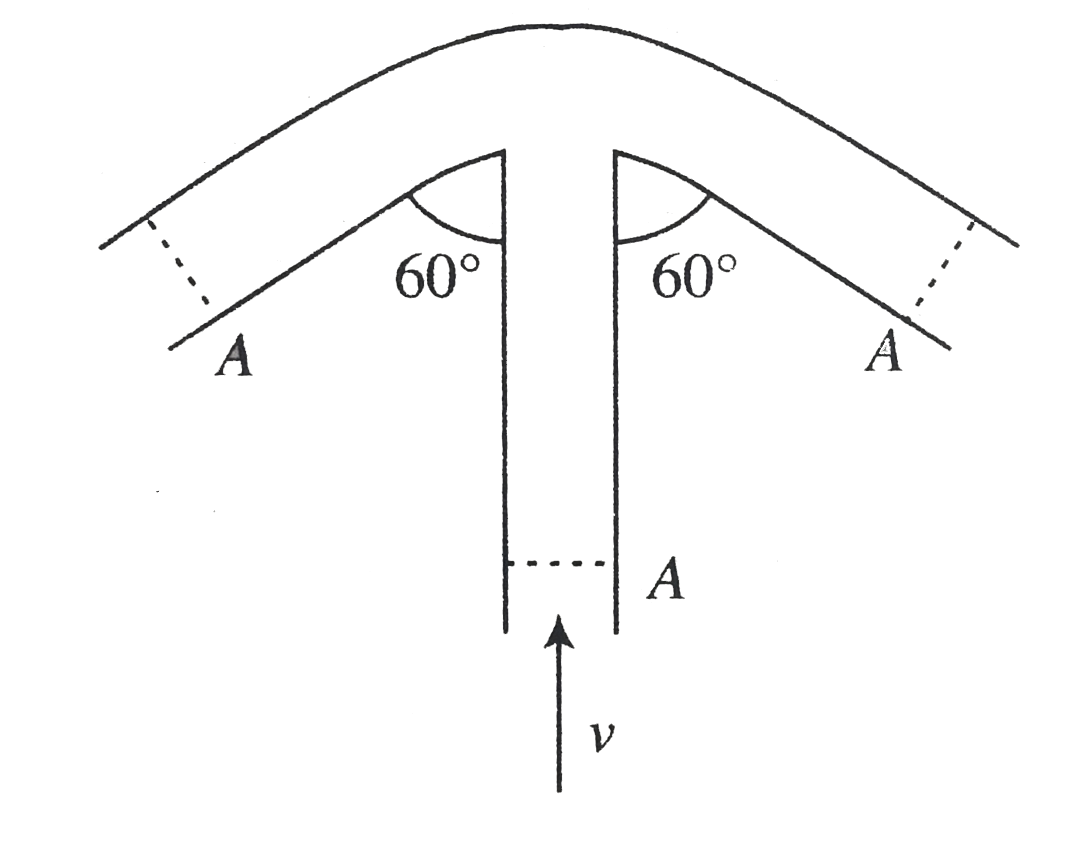
View SolutionAn ideal liquid of density ρ is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
View Solution

