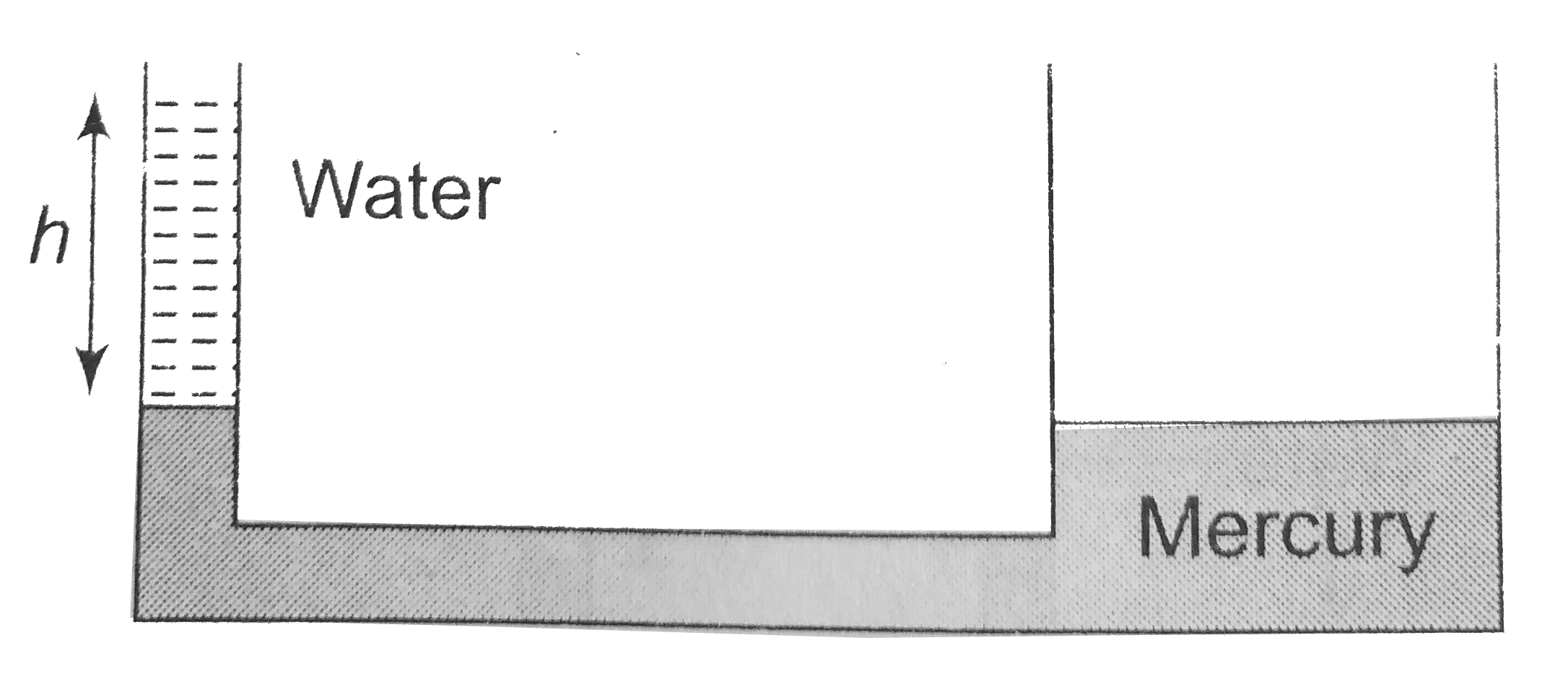
Two communicating vessels contain mercury. The diameter of one vessel in n times larger then the diameter of the other. A column of water of height h is poured into the left vessel. The mercury level will rise in the right hand vessel (s = relative density of mercury and ρ = density of water) by
n2h(n+1)2s
h(n2+1)s
h(n+1)2s
hn2s
The correct Answer is:B
(b) 
If the level in narrow tube goes down be h1 then in wider tube goes up to h2,
Now,πr2h1=π(nr)2h2⇒h1=m2h2
Now, pressure at point A = pressure at point B
Hρg=(h1+h2)ρ'g
⇒h=(n2h2+h2)sg((Ass=ρ'ρ)⇒h2=h(n2+1)s
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Buoyancy And Floatation40videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Continuity Equation And Bernoulli'S Theorem32videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
Similar Questions
Two communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height 70cm is poured into the narrow vessel. How much will the mercury level rise in the other vessel and how much will it sink in the narrow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is poured into the broad vessel?
View SolutionTwo cylindrcal vesels placed on a horizontal table contain water and mercury respectively up to the same height. There is a small hole in the walls of each of the vessels at half the height of liquids in the vessels. Find out the ratio of the velocities of efflux of water and mercury from the holes. Whcih of the two jets of liquid will fall at a greater distance on the table from the vessel? Relative density of mercury with respect to water = 13.6
View Solution
Knowledge Check
- Question 1 - Select One
in previous question, if 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relvative density of mercury = 13.6)
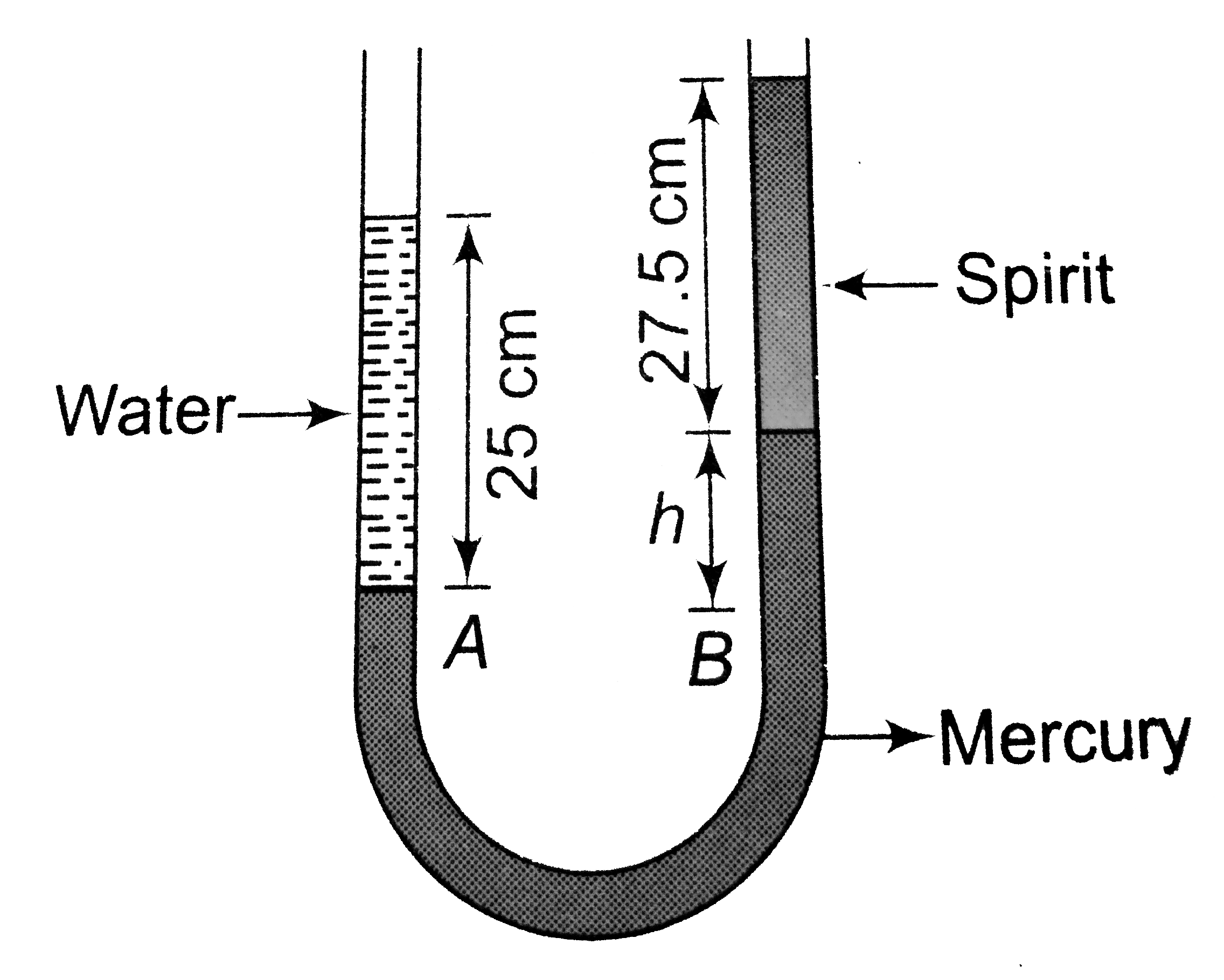A0.20 cmB0.22 cmC0.27c mD0.26cm - Question 2 - Select One
A cylindrical vessel 60 cm in diameter is partially filled with water. A sphere 30 cm in diameter is gently dropped into the vessel and is completely immersed. To what further height will the water in the cylinder rise ?
A15 cmB30 cmC40 cmD25 cm - Question 3 - Select One
An open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
A0.82 cmB1.35 cmC0.41 cmD2.32 cm
(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?View SolutionThe height of mercury which exerts the same pressure as 20 cm of water column, is
View SolutionA steel ball floats in a vessel with mercury. How will the volume of the part of the ball submerged in mercury change if a layer of water completely covering the ball is poured above the mercury?
View SolutionThe temperature of an air bubble while rising from bottom to surface of a lake remains constant but its diameter is doubled if the pressure on the surface is equal to h meter of mercury column and relative density of mercury is then the depth of lake in metre is -
View SolutionA cylinder of iron floats vertically and fully immersed in a vessel containing mercury and water. Find the ratio of the length of the cylinder immersed in water to that immersed in mercury. (Relative density of mercury = 13.6 and that of iron = 7.78)
View Solution