Distance of the centre of mass of a solid uniform cone from its vertex is $z_{0}$ . If the radius of its base is R and its height is h then $z_{0}$ is equal to:

A

$\frac{h^{2}}{4 R}$

B

$\frac{3 h}{4}$

C

$\frac{5 h}{8}$

D

$\frac{3 h^{2}}{8 R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let distnace of c.m from the vertex, $Z_{0} = y_{c m}$

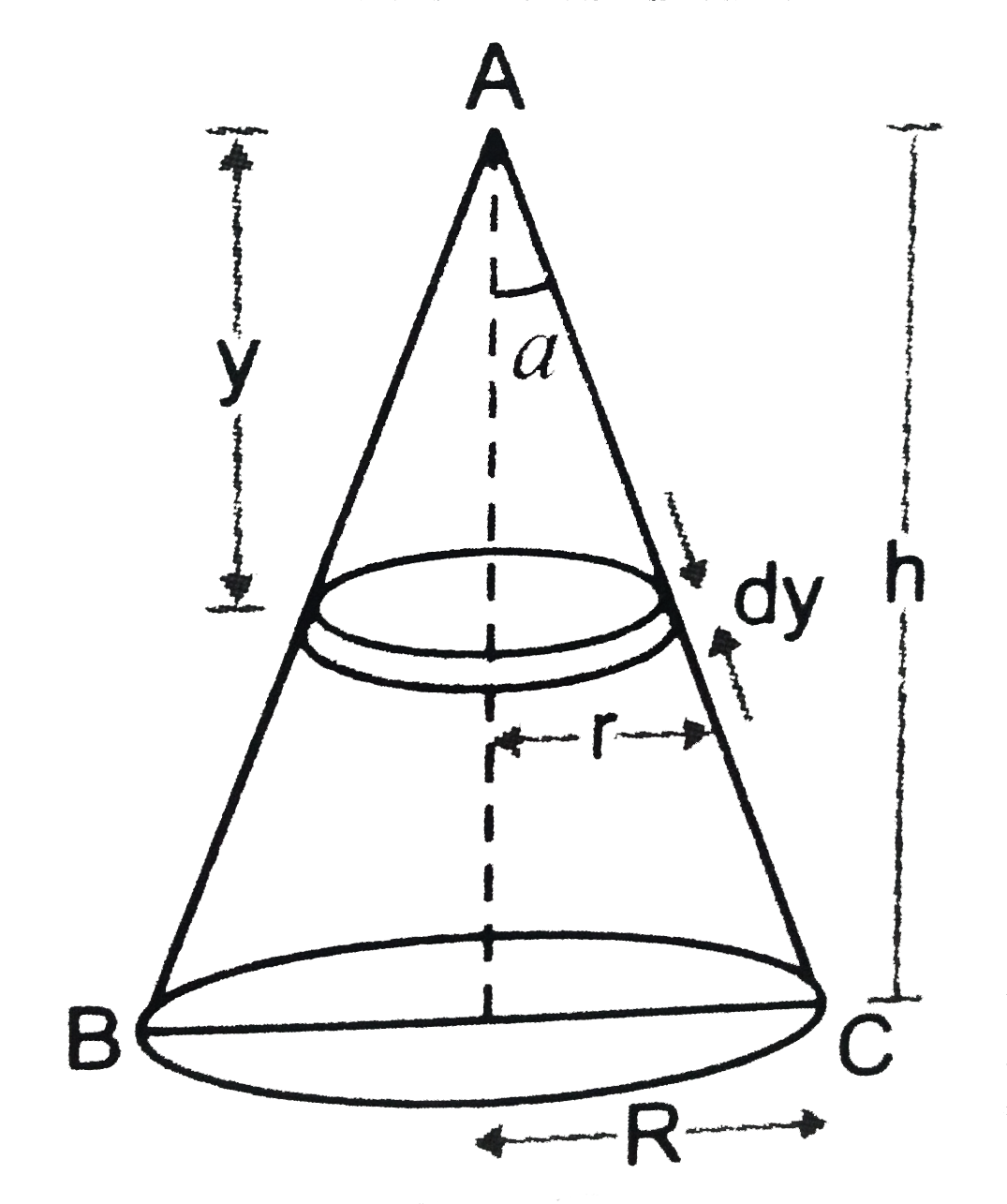
Let density of cone $= ρ$
$Z_{0} = y_{c m} = \frac{\int y d m}{\int d m}$
$= \frac{\int_{0}^{h} y π r^{2} d y ρ}{\frac{1}{3} π R^{2} h ρ} = \frac{\int_{0}^{h} r^{2} y d y}{\frac{1}{3} R^{2} h}$ ..(i)
As $\frac{r}{R} = \frac{y}{h}, ∴ r = \frac{y}{h} R$ , putting value of y in (i)
$Z_{0} = y_{c m} = \frac{\int_{0}^{h} 3 y^{3} d y}{h^{3}} = \frac{3 {[\frac{y^{4}}{4}]}_{0}^{h}}{h^{3}} = \frac{3}{4} h$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Distance of the centre of mass of a solid uniform cone from its vertex is $z_{0}$ . If the radius of its base is R and its height is h then $z_{0}$ is equal to:
A $\frac{b^{2}}{4 R}$
B $\frac{3 b}{4}$
C $\frac{5 h}{8}$
D $\frac{3 h^{2}}{8 R}$
Question 2 - Select One
The centre of mass of a solid cone along the line form the center of the base to the vertex is at
AOne-fourth of the height
BOne-third of the height
COne-fifth of the height
DNone of these
Question 3 - Select One
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
A $\frac{R}{2}$
B $\frac{R}{3}$
C $\frac{2 R}{2}$
D $\frac{2 R}{3}$

PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-Focus Multiple Choice Questions I.

Distance of the centre of mass of a solid uniform cone from its vertex...
01:59

Home
Ask Doubt
Profile