Three identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
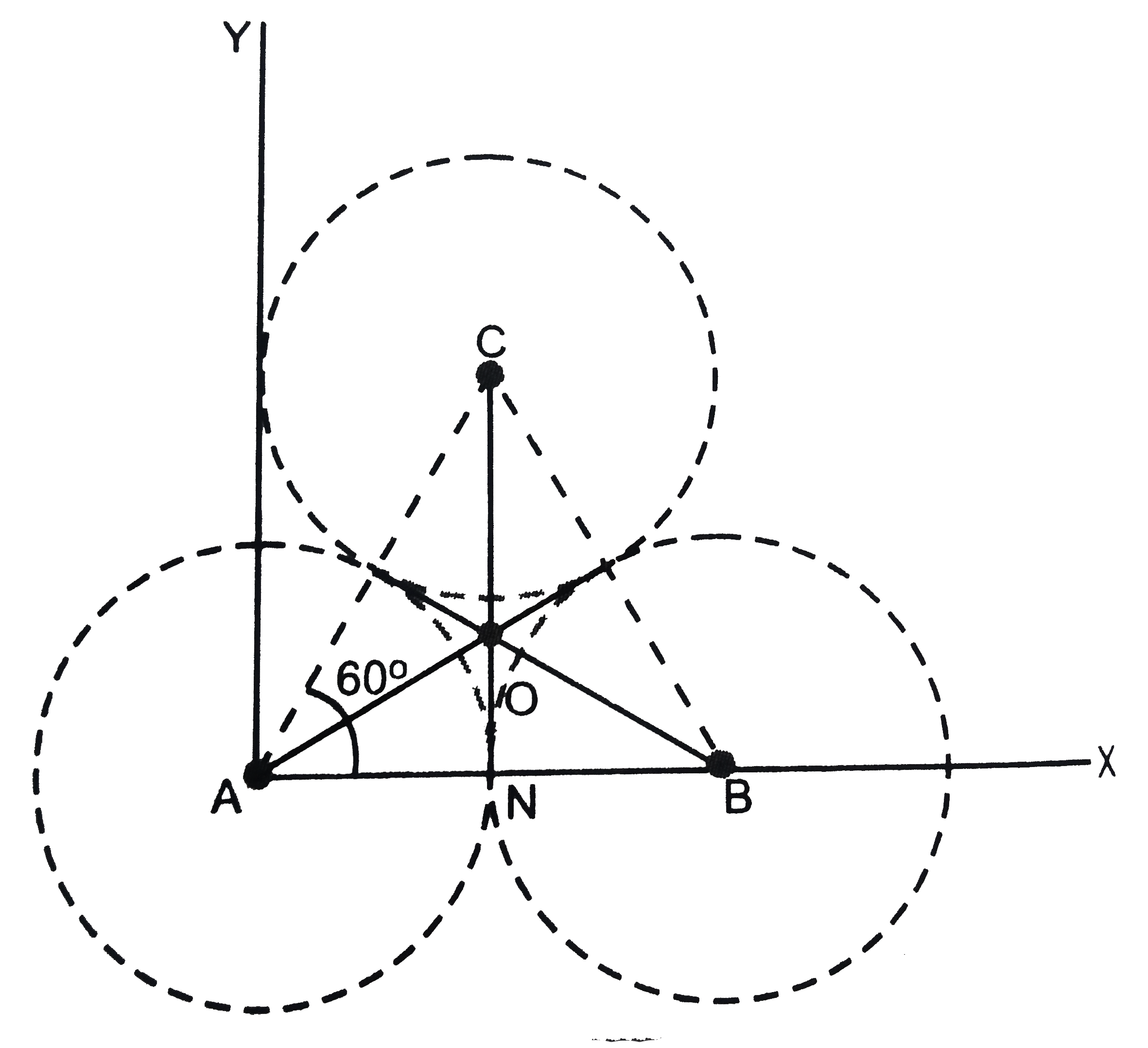
The centre of three spheres lie at the vertices A,B,C of an equilibrium triangle, Fig. Centre of mass is at the centroid of ΔABC.
Taking A as the origin, the co-ordinates of the three vertices of the triangle are :
A(x1,y1)=0,0,B(x2,y2)=2r,0
and C(x3,y3)=r,r√3
∴ Co-ordinates of centre of mass O are
x=m(x1+x2+x3)3m=0+2r+r3=r
y=m(y1+y2+y3)3m=0+0+r√33=r√3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE E
Explore 1 Video
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:MULTIPLE CHOICE QUESTIONS-I
Explore 1 Video
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE C
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Determine the position of the centre of mass of a hemisphere of radius R.
View SolutionThree identical spheres each of mass M and radius R are arranged in a row touching each other and their centres collinear.The moment of inertia of the system about an axis passing through the centre of the middle sphere and perpendicular to the line joining their centres is "
View Solution
Knowledge Check
Three identicle particle each of mass 1kg are placed with their centres on a straight line. Their centres are marked A,BandC respectively. The distance of centre of mass of the system from A is.
AKL+KM+LM3BKL+KM3CKL+LM3DKM+LM3Three identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
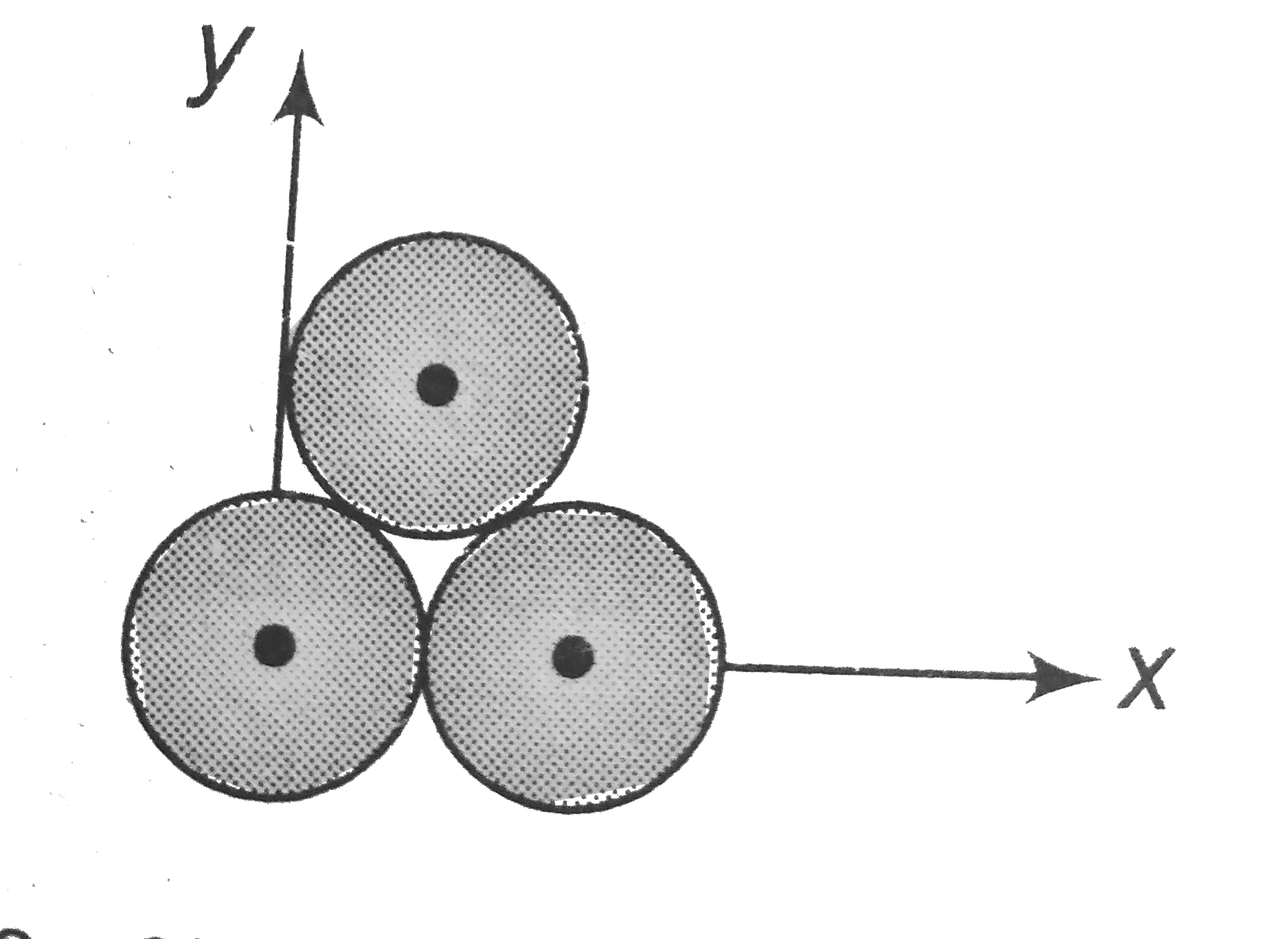 .A(R,R)B(0,0)C(R2,R2)D(R,R√3)
.A(R,R)B(0,0)C(R2,R2)D(R,R√3)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
Three identical particles each of same mass are placed touching each other with their centres on a straight line.Their centres are at A,B,and C respectively.Then distance of centre of mass of the system from A is
View SolutionThree identical spheres, each of mass 1 kg are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked P, Q, R respectively, the distance of centre of mass of the system from P (origin) is
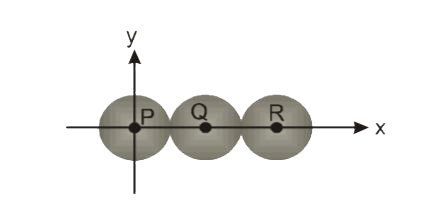
View SolutionFour identical bodies each of mass 1 kg are placed touching to each other with centres on a straight line. If their centres are marked A, B, C and D respectively, then the distance of centre of mass of the system from B will be

View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View Solution

