The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
The correct Answer is:B
At x=±xm the particle tuns back. Therefore, its stone II reaches the bottom earlier than stone I. K=0. The total energy E is in the form of potential energy i.e.V=E.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:JEE (Main and Advanced)
Explore 82 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Comprehension
Explore 9 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Problems For Practice
Explore 76 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
The energy of a particle executing simple harmonic motion is given by E=Ax2+Bv2 where x is the displacement from mean position x=0 and v is the velocity of the particle at x then choose the correct statement(s)
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View Solution
Knowledge Check
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
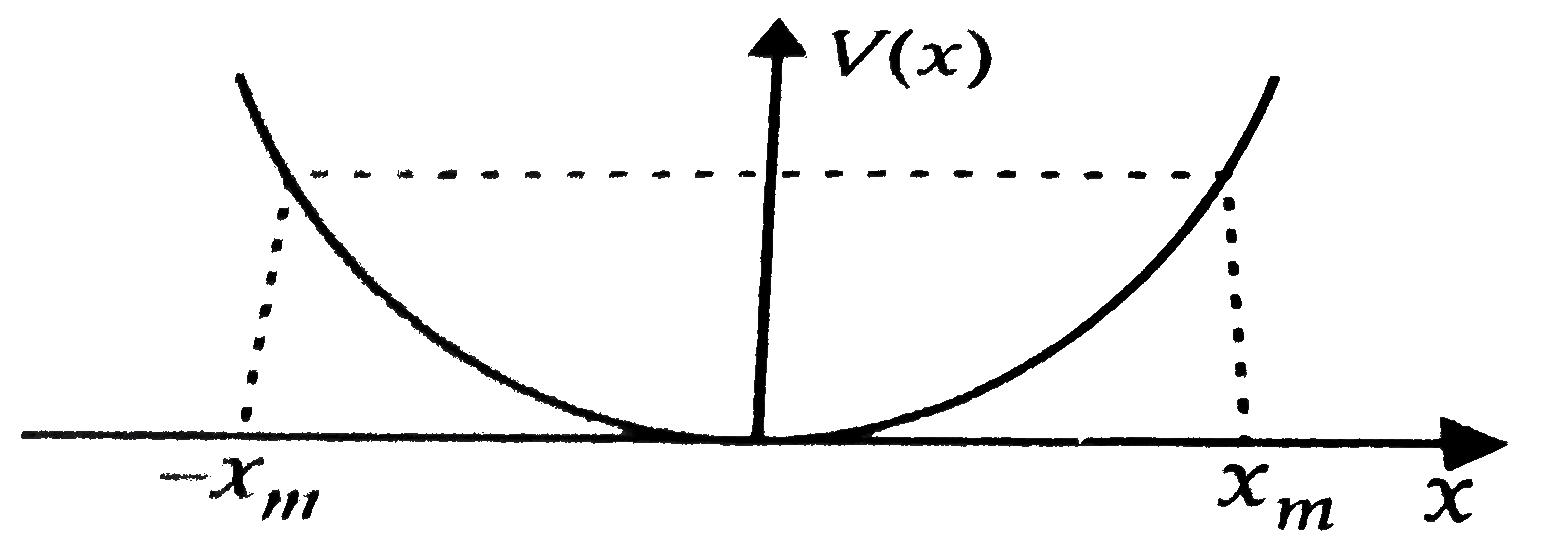 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt EThe potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
A√xBxCx2Dx3The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.A(a) independent of x.B(b) ∝x2C(c ) prop xD(d) propx^(1//2)
A particle is executing simple harmonic motion between exterme positions given by (−1,−2,−3)cm and (1,2,1)cm. Its amplitude of oscillation is
View SolutionThe potential energy of a particle with displacement X is U(X). The motion is simple harmonic, when (K is a positive constant)
View SolutionConsider the following statements. The total energy of a particle executing simple harmonic motion depends on its
(1) Amplitude
(2) Period
(3) Displacement Of these statements
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0andU=0 for x≥0. If total mechanical energy of the particle is E, is speed at x=√2Ek is
View SolutionThe potential energy of a 1kg particle free to move along the x-axis is given by V(x)=(x44−x22)J The total mechanical energy of the particle is 2J then the maximum speed (∈m/s) is
View Solution

