The motion of a particle of mass m is given by x=0 for t<0s,x(t)=Asin4πt for 0<t<(14)s(A>0),and x=0 for t>(14)s.
The force at t=(1/8) s on the particle is 16π2Am
The particle is acted upon by an impulse of magnitude 4π2Am at t=0s and t=(1/4)s
The particle is not acted upon by any force
The particle is not acted upon by a constant force
The correct Answer is:a,b,d
Here, x=0, for t<0s
x(t)=Asin4πt for 0<t<14s
x=0 for t>14s
For 0<t<14s
υ(t)=dxdt=4πAcos4πt,a(t)=dυdt−16π2Asin4πt
At t=18sa(t)=−16π2Asin4π×18=−16π2A×1
F=ma(t)=−16π2Am
Impulse = change in linear momentum) at t=0 is same as at t=14sec
Further as F depends on A which is not constant therefore the particle is not acted upon by a constant force .
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Fill in the blanks
20 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Problems for practice
112 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Value Based Questions with Answers
5 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View SolutionFig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View Solution
Knowledge Check
The motion of a particle of mass m is given by x=0 for t<0 s, x (t) = Asin4πtfor0<t(1/4)s(A>0) and x=0 for t>(1/4) s Which of the following statement(s) is (are) true?
AThe force at t=(1/8) s on particle is −16π2 A-mBThe particle is acted upon by an impulse of magnitude (4π2A−m) at t=0 s and t=(1/4) s.CThe particle is not acted upon by any forceDThe particle is not acted upon by a constant forceFigure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
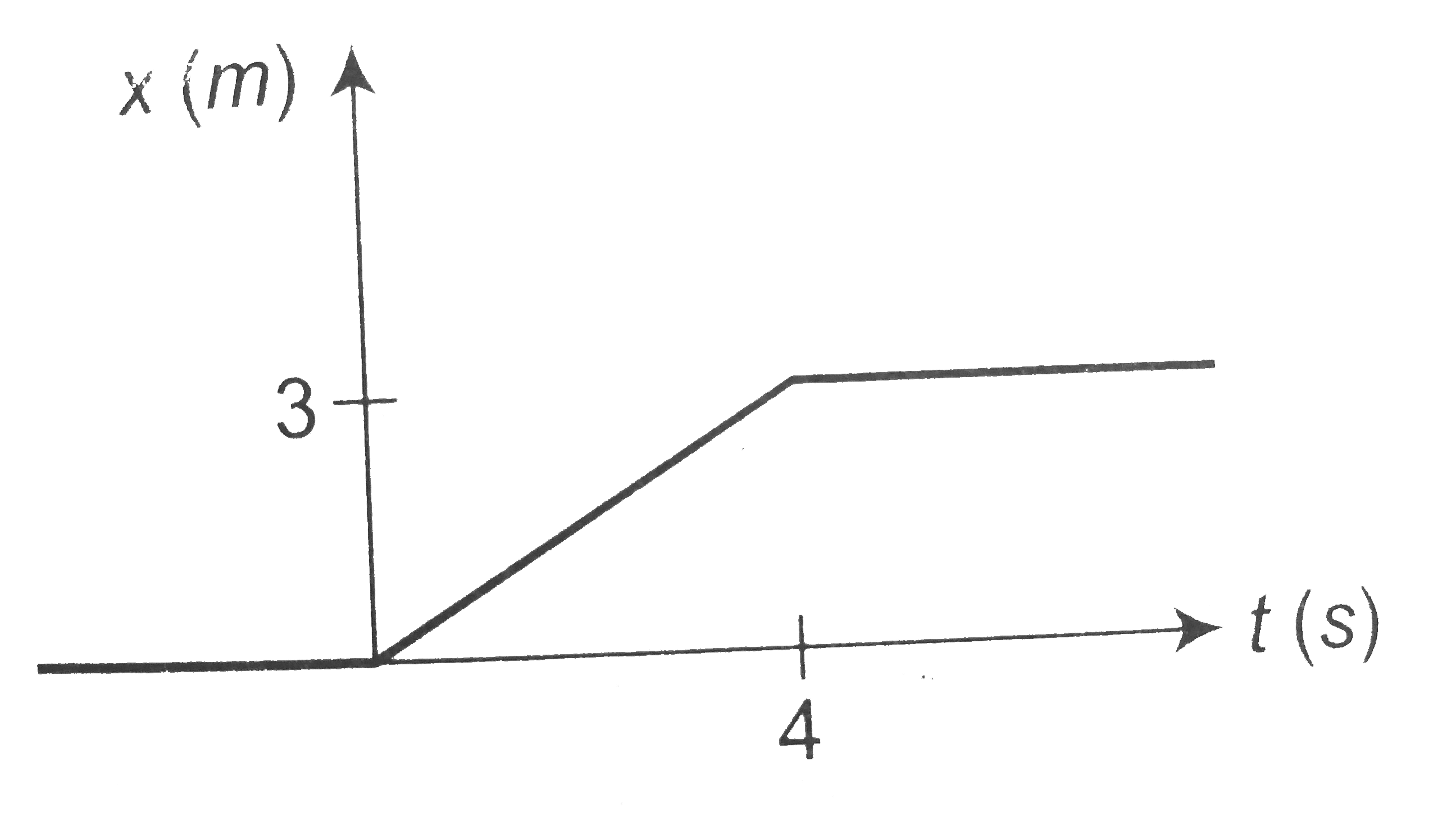 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3The equation of linear S.H.M. of a particle is given by x=0.5sin[4πt−π3], the term π3 represents
Athe phase of S.H.M.Bthe initial of S.H.M.Cangular frequency of S.H.M.Dperiod of S.H.M.
Shown the position time graph of a particle of mass 4 kg What is the force on the particle for t<0,0<t<4s motion only
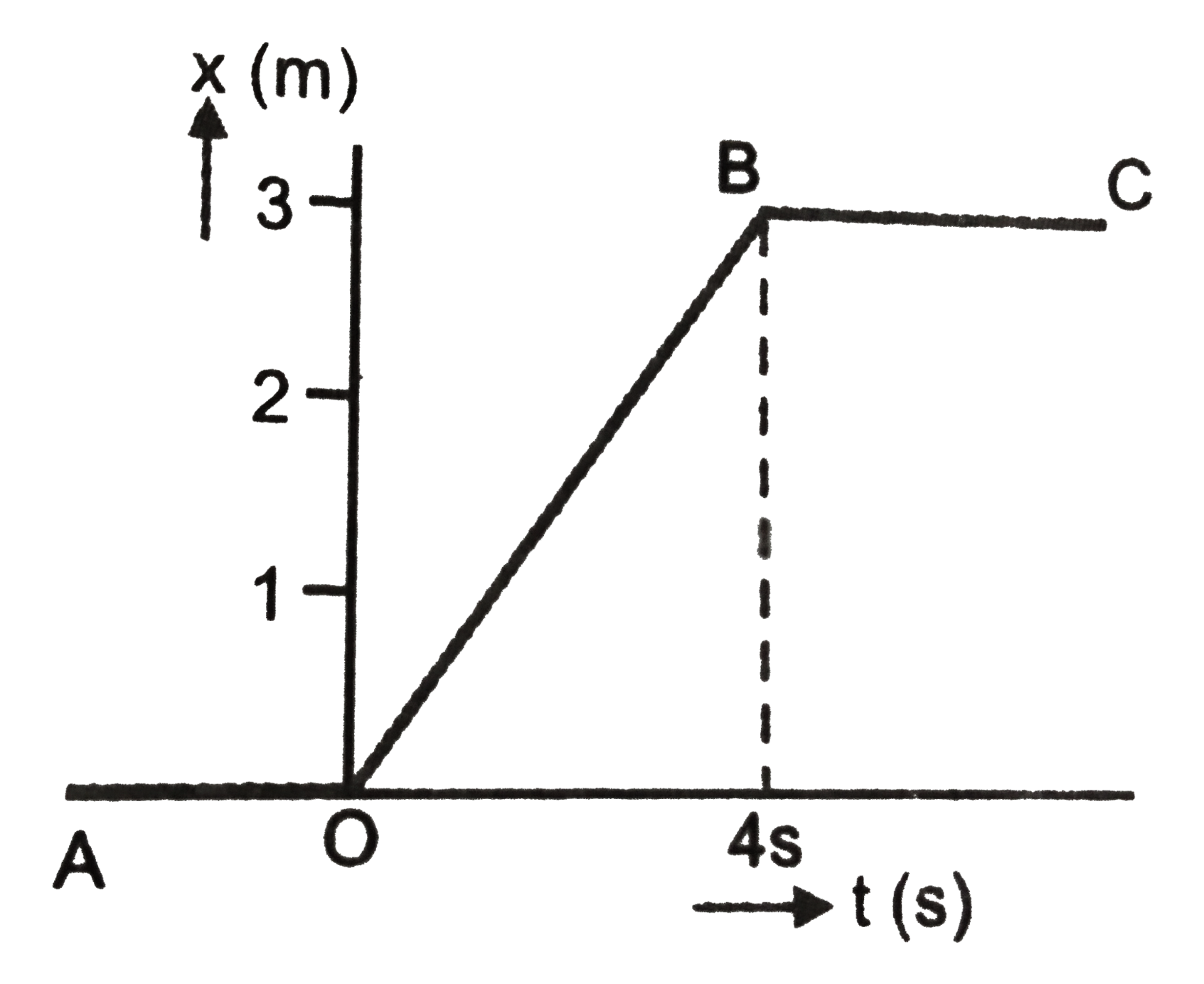 .
.
View SolutionThe displacement of a particle of mass 0.1 kg from . its mean position is given by, y = 0.05 sin 4π(5t+0.4) (where all the quantities are in S.I. unit). Period of motion is 0.1 s. The total energy of the particle is
View SolutionThe equation of a wave on a string of linear mass density 0.04kgm−1 is given by y=0.02(m)sin[2π(t0.04(s)−x0.50(m))]. The tension in the string is :
View Solutionthe equation of a wave on a string of linear mass density 0.04kgm−1 is given by
y=0.02(m)sin[2π(t0.04(s)−x0.50(m))].
Then tension in the string is
View SolutionThe acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
View Solution
