Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.
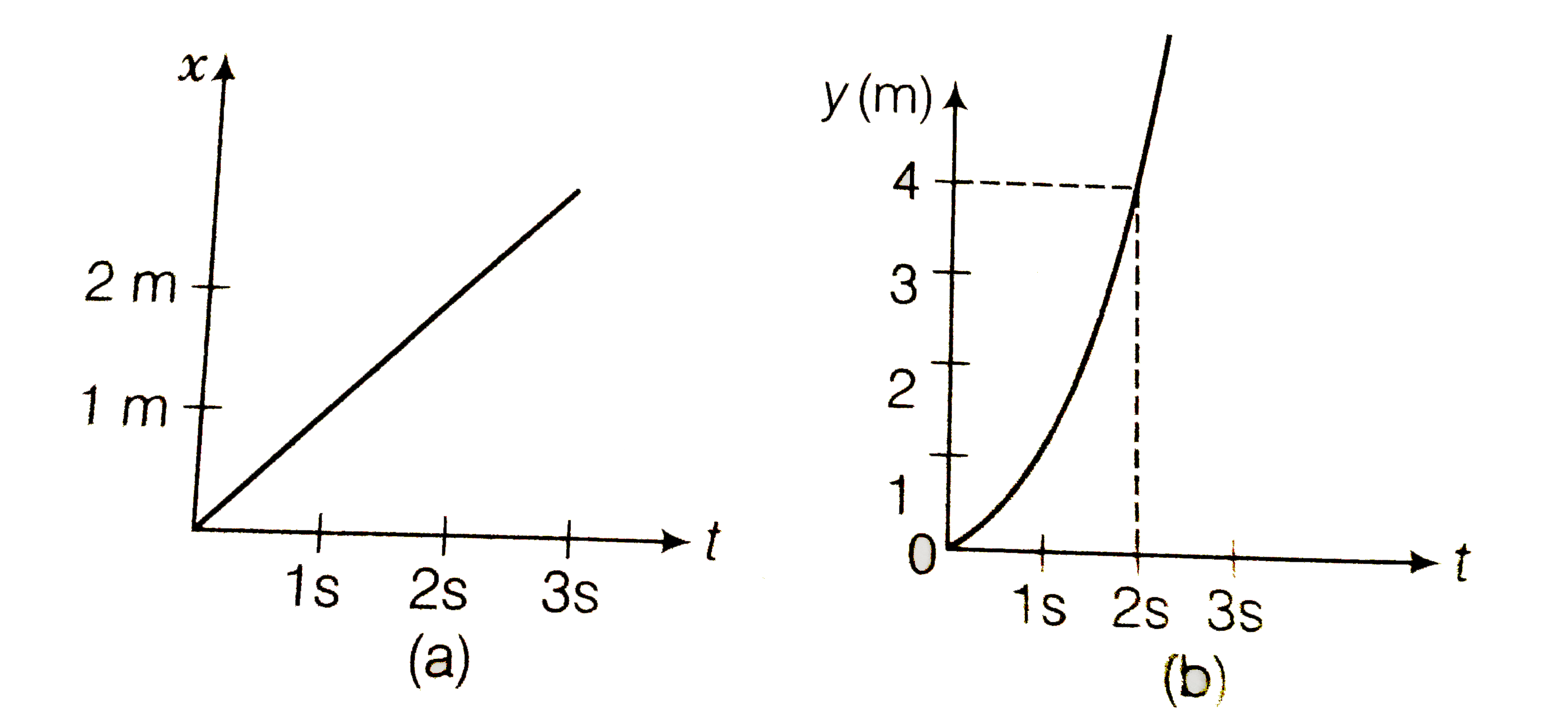
If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
As (x,t) diagram of particle is a st line , motion along X-axis is unifrom
From x=ut,u=xt=22=1m/s
Force along X-axis is zero
The (y,t) diagram is a parabola. If a is unifrom acceleration along Y-axis then from y=12at2
4=12ax22,a=2m/s2
As F=ma∴F=5001000×2=1N along Y-axis .
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Higher order thinking skills
Explore 10 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Value Based Questions with Answers
Explore 5 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Additional Examples / Exercises
Explore 6 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.

If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
View Solution

Figure shows (vx,t) and (vy,t) diagram for a body of unit mass. Find the force as a function of time.
View Solution
Knowledge Check
If a particle moves 5m in +x- direction. Show the displacement of the particle-
A5ˆjB5ˆiC−5ˆjD5ˆkThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 A(a) 300JB(b) −300JC(c) 400JD(d) −400J
A(a) 300JB(b) −300JC(c) 400JD(d) −400JThe motion of a particle of mass (m) is described by y=ut+12gt2 . Find the force acting on the particle
A2 mg,BmgCmg2,D4mg
In the given figure, find the force acting on a particle of mass 1 kg.
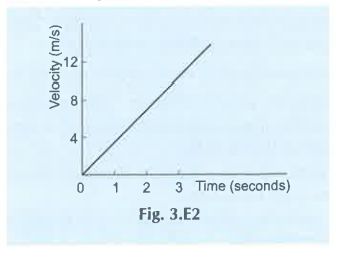
View SolutionFigure 3.E2 shows the velocity -time graph for a particle moving in a fixed direction. Find the acceleration of the particle.
View SolutionThe motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
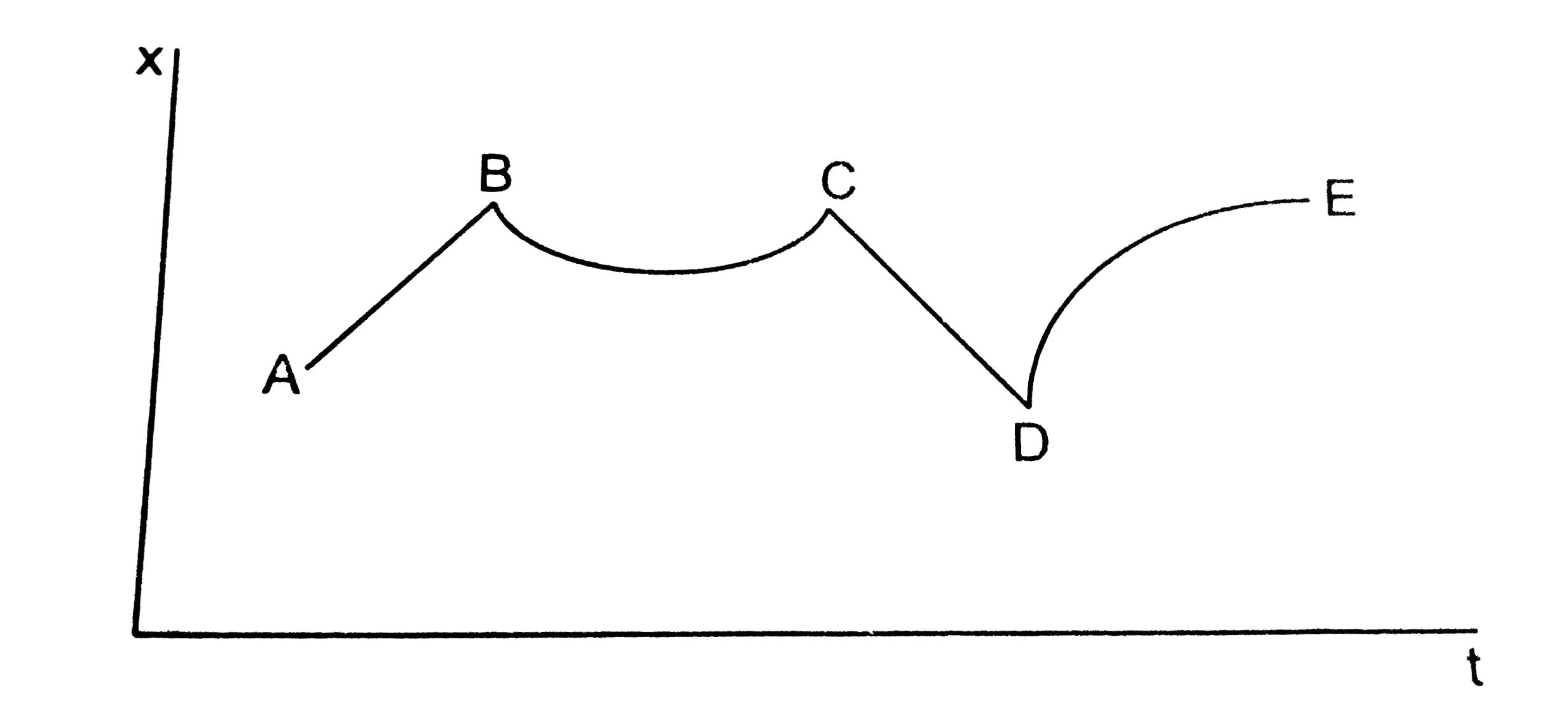
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View Solution

