In the given figure, find the force acting on a particle of mass 1 kg.
The correct Answer is:Zero
To find the force acting on a particle of mass 1 kg in the given configuration, we will analyze the gravitational forces acting on it due to the other masses around it.
1. Identify the Masses and Distances:
- We have a mass of 1 kg (let's call it m1) and it is surrounded by other masses: two 2 kg masses (let's call them m2) and another 1 kg mass (let's call it m3).
- The distances between the masses are given as follows: the distance between m1 and m2 is 1 meter, and the distance between m1 and m3 is also 1 meter.
2. Calculate the Gravitational Force:
- The gravitational force between two masses is given by Newton's law of gravitation:
F=G⋅m1⋅m2r2
- Here, G is the gravitational constant, m1 is the mass of the particle (1 kg), m2 is the mass of the other particles (2 kg), and r is the distance between them (1 meter).
3. Calculate Forces in the X-Direction:
- For the forces acting on m1 due to the two 2 kg masses:
- The force from one 2 kg mass (let's say to the right) is:
Fx1=G⋅1⋅212=2G
- The force from the other 2 kg mass (to the left) is:
Fx2=G⋅1⋅212=2G
- Since these forces are equal and opposite, they cancel each other out:
Fx net=2G−2G=0
4. Calculate Forces in the Y-Direction:
- Now consider the forces acting in the y-direction:
- The force from the 1 kg mass (let's say above) is:
Fy1=G⋅1⋅112=G
- The force from the other 1 kg mass (below) is:
Fy2=G⋅1⋅112=G
- Again, these forces are equal and opposite, so they cancel each other out:
Fy net=G−G=0
5. Calculate the Net Force:
- Since both the net forces in the x-direction and y-direction are zero:
Fnet=Fx net+Fy net=0+0=0
Conclusion:
The net force acting on the particle of mass 1 kg is 0 N.
- We have a mass of 1 kg (let's call it m1) and it is surrounded by other masses: two 2 kg masses (let's call them m2) and another 1 kg mass (let's call it m3).
- The distances between the masses are given as follows: the distance between m1 and m2 is 1 meter, and the distance between m1 and m3 is also 1 meter.
- The gravitational force between two masses is given by Newton's law of gravitation:
F=G⋅m1⋅m2r2
- Here, G is the gravitational constant, m1 is the mass of the particle (1 kg), m2 is the mass of the other particles (2 kg), and r is the distance between them (1 meter).
- For the forces acting on m1 due to the two 2 kg masses:
- The force from one 2 kg mass (let's say to the right) is:
Fx1=G⋅1⋅212=2G
- The force from the other 2 kg mass (to the left) is:
Fx2=G⋅1⋅212=2G
- Since these forces are equal and opposite, they cancel each other out:
Fx net=2G−2G=0
- Now consider the forces acting in the y-direction:
- The force from the 1 kg mass (let's say above) is:
Fy1=G⋅1⋅112=G
- The force from the other 1 kg mass (below) is:
Fy2=G⋅1⋅112=G
- Again, these forces are equal and opposite, so they cancel each other out:
Fy net=G−G=0
- Since both the net forces in the x-direction and y-direction are zero:
Fnet=Fx net+Fy net=0+0=0
The net force acting on the particle of mass 1 kg is 0 N.
Topper's Solved these Questions
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
Explore 50 Videos
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
Explore 20 Videos
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 16 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 13 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
Similar Questions
Three equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThe gravitationasl fiedl in a region is given by →E=(5Nkg−1)→i+(12nk−1)→j.. a.find the magnitude of the gravitational force acting on a particle of mass 2 kg th gravittional fore actiing on a particle of mass 2 kg placed at the origin. B. Find the potential at teh points (12m,0) and (o,5m) if the potential at teh origin is taken to be zero. C. Find the change in gravitationa potential energyif a particle of mass 2 kg is taken from the origin to teh point (12m,5m). d. Find the change in potential energy if the particle is taken from (12m,0) to (0,5,m).
View Solution
Knowledge Check
In the figure given, the position-time graph of a particle of mass 0.1 kg is shown the impulse at t = 2s is
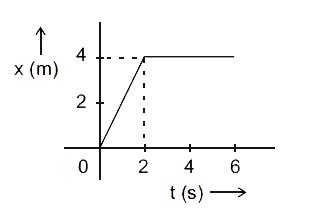 A0.2 kg m/sB−0.2 kg m/sC0.1 kg m/sD−0.4 kg m/s
A0.2 kg m/sB−0.2 kg m/sC0.1 kg m/sD−0.4 kg m/s
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle isA4s−1B(52π)s−1C(18π)s−1D(12π)s−1The displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
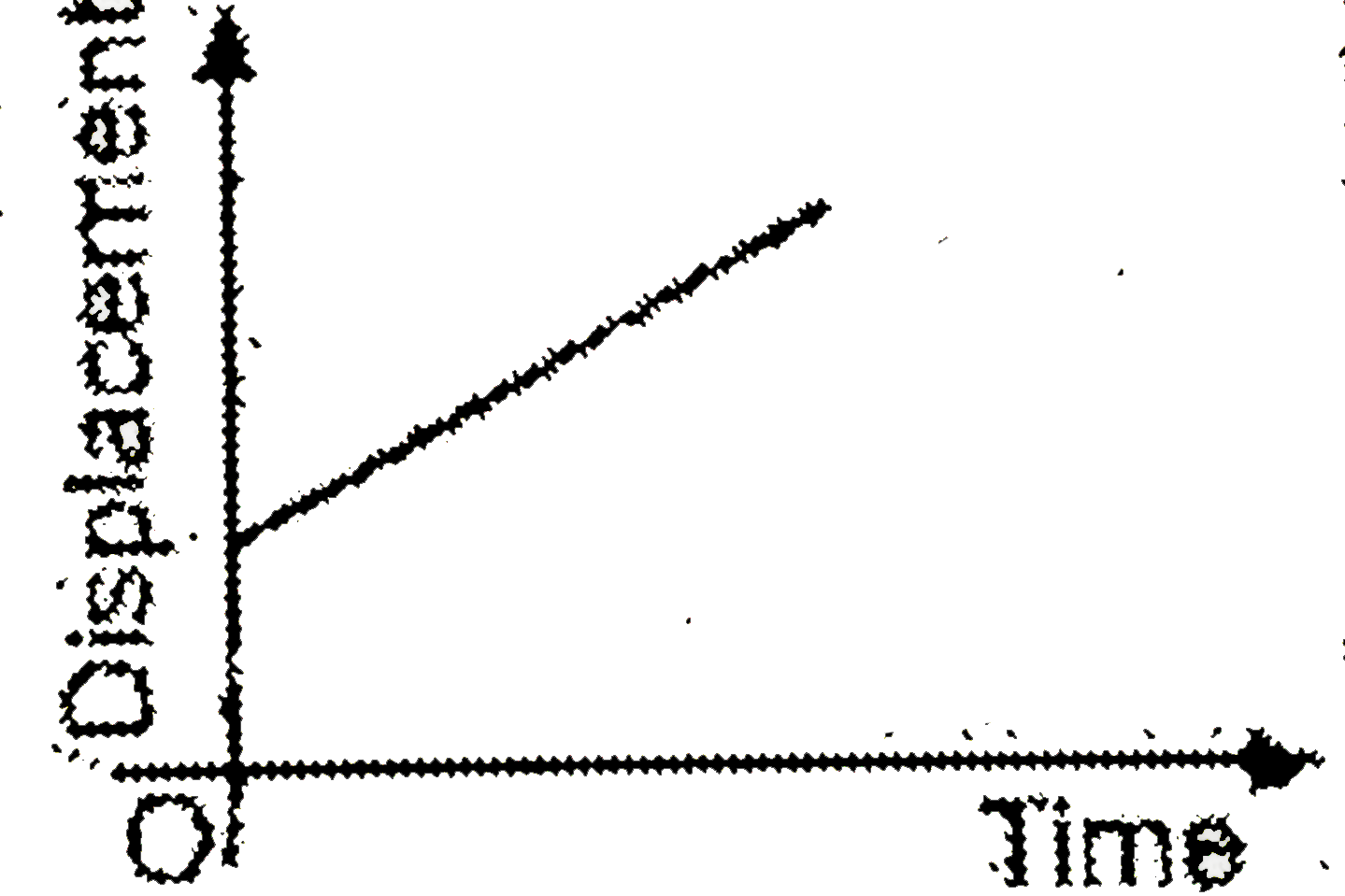 AActing at the beginning part of motionBZeroCNot zeroDNone of these
AActing at the beginning part of motionBZeroCNot zeroDNone of these
A time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View SolutionIn the figure given below, the position–time graph of a particle of mass 0·1 kg is shown. The impulse at t=2sec is
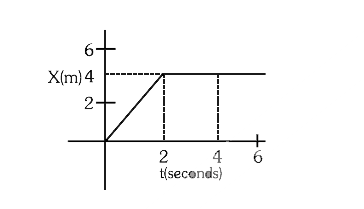
View SolutionIn the figure given below, the position time graph of a particle of mass 0.1kg is shown. The impulse at t=2 sec is

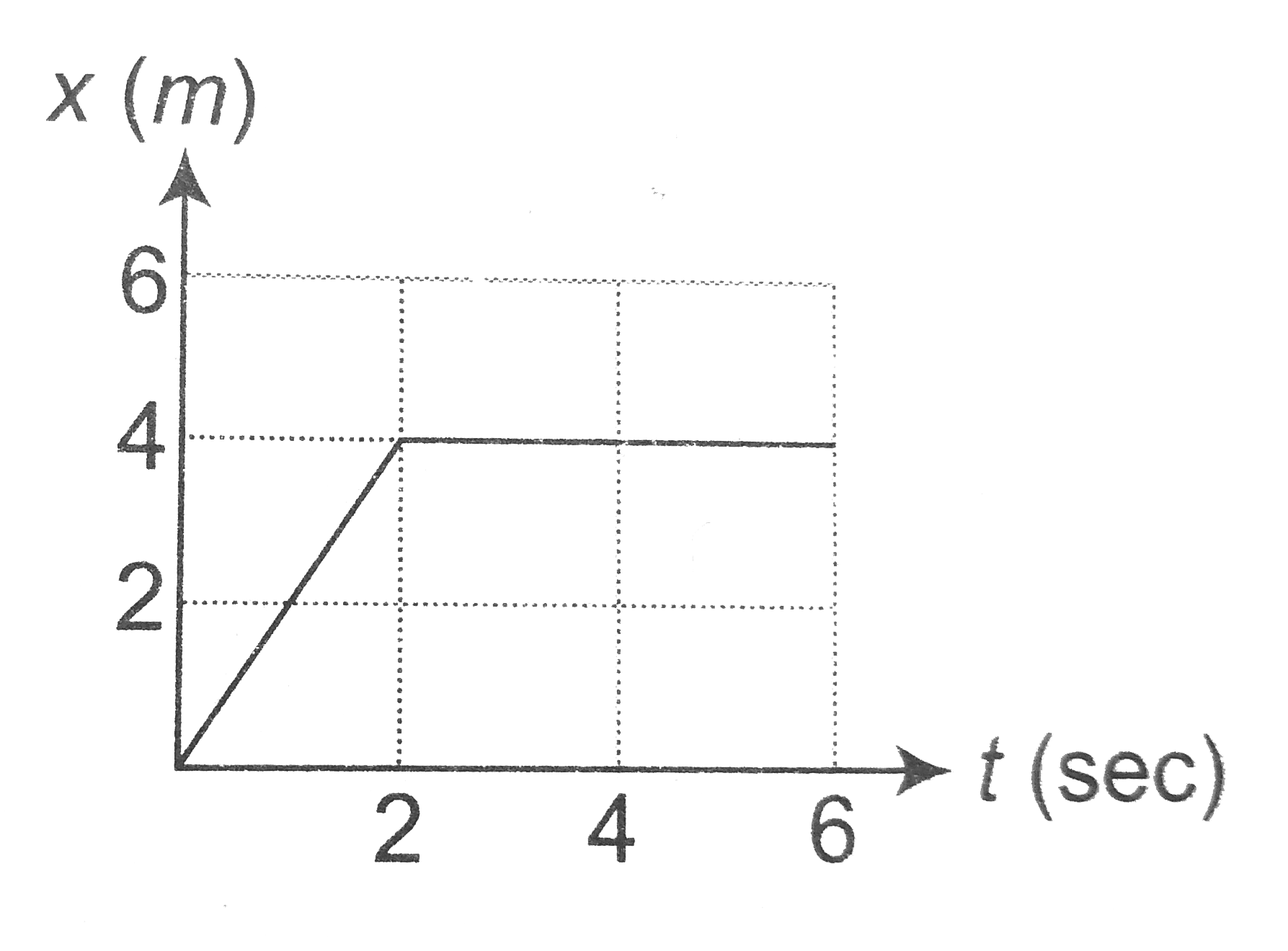
View SolutionIn the figure given below, the position-time graph of a particle of mass 0.1kg is shown. The impuslse at t=2 sec is
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View Solution

