An aeroplane is flying with velocity →vp(=100ms−1 towards East)
with respect to ground through motionless air and →vw is the wind velocity with respect ot ground. The total velocity of aeroplane is →v=→vP+→vw
The magnitude of the velocity is often called speed . the heading of the plane is the direction in which the nose of the plane is the direction is which th nose fo the plane points. In fact, it is the direction in which the engine propels the plane . Abswer the following questions :
If the wind blow with velocity 25ms−1 Norhtwards, the plane velocity is deflected from East by an angle.
sin−1(25/100)
cos ^(-1) (25 //100)
tan−1(25/100)
cot^(-1) ( 25 //100)
The correct Answer is:A
Refer to Gig. 2 (CF) . 74, as the resultant velocity is along OC, so the plane velocity w.r.t ground must be along OB, Here,
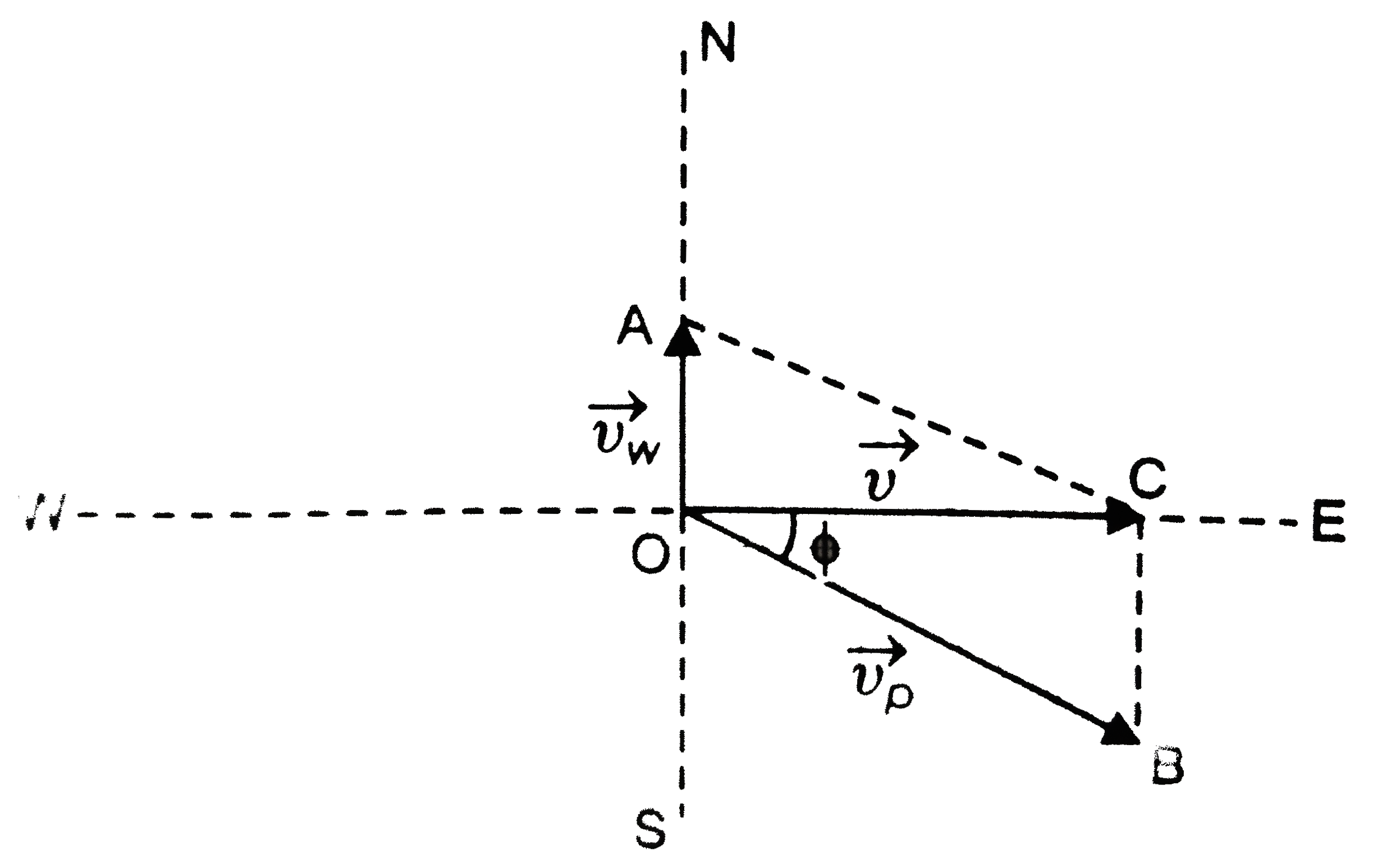 .
.
1 v_p = 100 ms^(-1) and v_w = 25 ms^)-1).
In ΔOCB,
sinϕ=CBOB=vwvp=25100or phi = sin^(-1) ((25)/(100)).
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 NCERT Integer type
Explore 4 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Assertion-Reaseon Type
Explore 14 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:3 NCERT multiple
Explore 161 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A particle moving in the xy plane experiences a velocity dependent force →F=k(vyˆi+vxˆj), where vxandvy are the x and y components of its velocity →v . If →a is the acceleration of the particle, then which of the following statements is true for the particle?
View SolutionLet →uand→v be unit vectors such that →u×→v+→u=→w and →w×→u=→v. Find the value of [→u→v→w].
View Solution
Knowledge Check
An aeroplane is flying with velocity →vp=100ms−1 towards East
with respect to ground through motionless air and →vw is the wind velocity with respect of ground. The total velocity of aeroplane is →v=→vP+→vw
The magnitude of the velocity is often called speed . the heading of the plane is the direction in which the nose of the plane points. In fact, it is the direction in which the engine propels the plane . Answer the following questions :
If θ is the answer to question 156, the total speed of the plane in ms−1 is.A100sinθB100cosθC100cosecθD100secθA car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
AWestBNorthCN-WDS-WAn aeroplane is flying with the velocity of V1=800kmph relative to the air towards south.A wind with velocity of V2=15ms−1 is blowing from west to east.What is the velocity of the aeroplane with respect of the earth.
A221.7ms−1B150ms−1C82ms−1D40ms−1
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
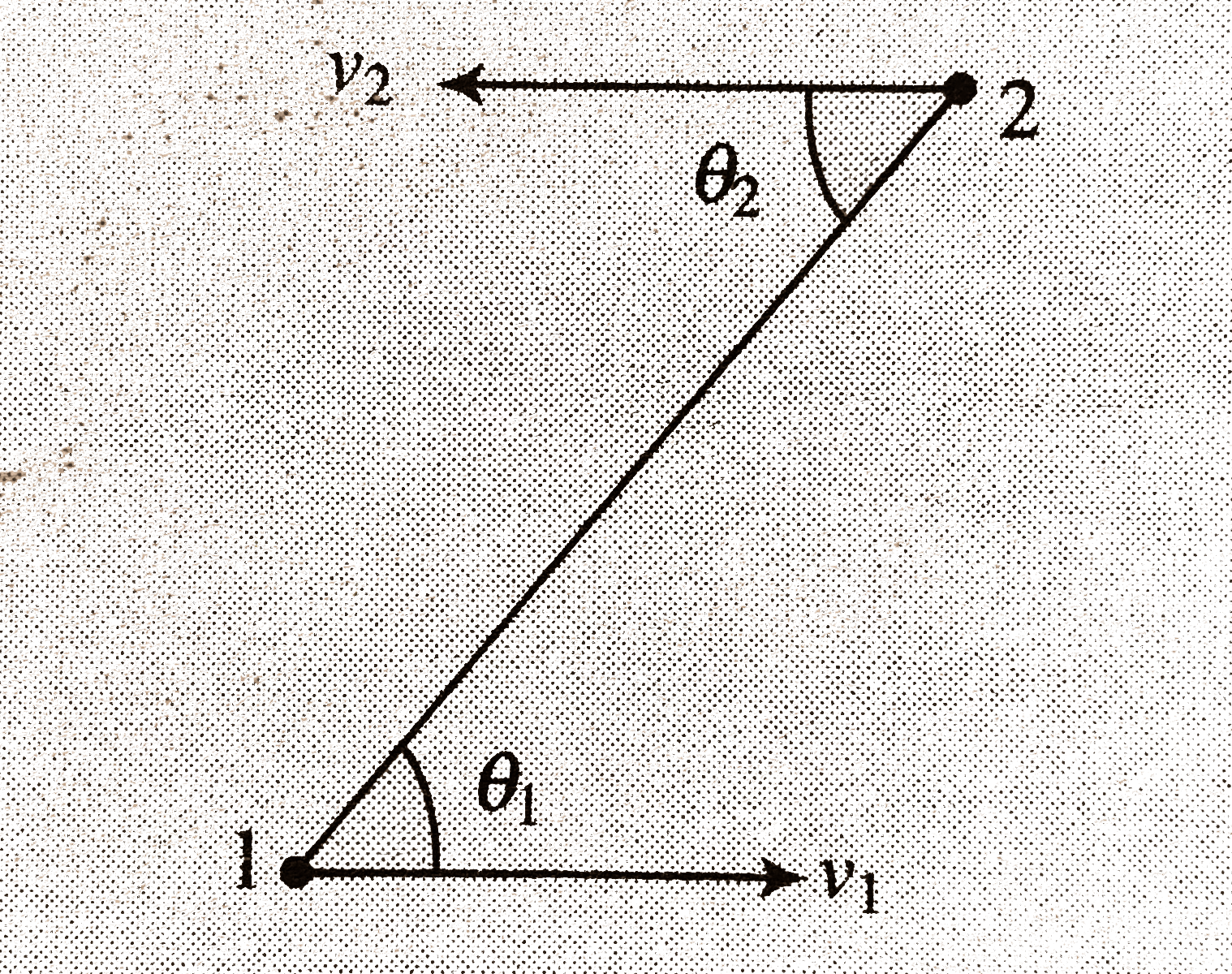 .
.
View SolutionAn electron is travelling with velocity →v=3ˆi+5ˆjms−1 in a magnetic field tesla. What is the magnitude and direction of the force →F acting on the electron?
View SolutionThe linear velocity of a particle on a rotating body is given by →v=→ω×→r where →ω is the angular velocity and →r is the radius vector. What is the value of |v| if →ω=ˆi−2ˆj+2ˆkand→r=4ˆj−3ˆk ?
View SolutionAn electron is launched with velocity →v in a uniform magnetic field →B. The angle θ between →vand→B lies between 0 and π2. Its velocity vector →v returns to its initial value in a time interval of
View SolutionThe velocity of a particle varies with time as per the law →v=→a+→b t where →a and →b are two constant vectors. The time at which velocity of the particle at t=0 is :
View Solution

