An object of mass 3kg is at rest. Now a force of →F=6t2ˆI+4tˆj is applied on the object, the velocity of object at t=3s is.
18ˆI+3ˆj
18ˆI+6ˆj
3 hat I + 1 8 hat j
18ˆI+4harj
The correct Answer is:B
To find the velocity of the object at t=3 seconds, we can follow these steps:
Step 1: Identify the given parameters
- Mass of the object, m=3kg
- Force applied, →F=6t2^i+4t^j
Step 2: Calculate the acceleration
Using Newton's second law, →F=m→a, we can find the acceleration →a:
→a=→Fm=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Step 3: Relate acceleration to velocity
Acceleration is the derivative of velocity with respect to time:
→a=d→vdt
Thus, we can write:
d→vdt=2t2^i+43t^j
Step 4: Integrate to find velocity
Integrating both sides with respect to time t:
→v=∫(2t2^i+43t^j)dt
This gives us:
→v=(23t3)^i+(23t2)^j+→C
Since the object is initially at rest, the constant of integration →C=0:
→v=23t3^i+23t2^j
Step 5: Calculate velocity at t=3s
Substituting t=3:
→v=23(33)^i+23(32)^j
Calculating each term:
→v=23(27)^i+23(9)^j
→v=18^i+6^j
Final Answer
The velocity of the object at t=3s is:
→v=18^i+6^jm/s
---
- Mass of the object, m=3kg
- Force applied, →F=6t2^i+4t^j
Using Newton's second law, →F=m→a, we can find the acceleration →a:
→a=→Fm=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Acceleration is the derivative of velocity with respect to time:
→a=d→vdt
Thus, we can write:
d→vdt=2t2^i+43t^j
Integrating both sides with respect to time t:
→v=∫(2t2^i+43t^j)dt
This gives us:
→v=(23t3)^i+(23t2)^j+→C
Since the object is initially at rest, the constant of integration →C=0:
→v=23t3^i+23t2^j
Substituting t=3:
→v=23(33)^i+23(32)^j
Calculating each term:
→v=23(27)^i+23(9)^j
→v=18^i+6^j
The velocity of the object at t=3s is:
→v=18^i+6^jm/s
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 NCERT multiple Choice
Explore 10 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 NCERT Integer type
Explore 4 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 NCERT multiple
Explore 15 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A body of mass 1kg is acted upon by a force →F=2sin3πˆi+3cos3πˆj.Find its position at t=1sec if at t=0 it is at rest at origin.
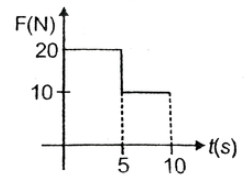
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t = 1s is will be F (N) 20 10 t(s) 10 5
View Solution
Knowledge Check
An object of mass 3 kg is at rest. Now a force F=6t2ˆj+2tˆj N is applied on the object. Find the velocity of the object at t=3 sec.
A18→i+3→jB18→i−3→jC3→i−18→jD3→i+18→jAn object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -A(3ˆi+2ˆj)m/sB(2ˆi+4ˆj)m/sC(4ˆi+4ˆj)m/sD(3ˆi−4ˆj)m/sA body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=6ˆi−12ˆjms−1, the time at which it will just have a velocity along the y-axis is :
AneverB10 sC2 sD15 s
Force is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=1 s will be
View Solution(a) At a certain instant, a particle-like object is acted on by a force →F=(4.0N)ˆi−(2.0N)ˆj+(9.0N)ˆk while the object's velocity is →v=−(2.0m/s)ˆi+(4.0m/s)ˆk. What is the instan-taneous rate at which the force does work on the object ? (b) At some other time, the velocity consists of only a y component. If the force is unchanged and the instantaneous power is -15 W, what is the velocity of the object ?
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionThe position of a particle is given by →r=3tˆi−4t2ˆj+5ˆk. Then the magnitude of the velocity of the particle at t = 2 s is
View SolutionA force →F=(3tˆi+5ˆj)N acts on a body due to which its position varies as →S=(2t2ˆi−5ˆj). Work done by this force in initial 2s is:
View Solution

