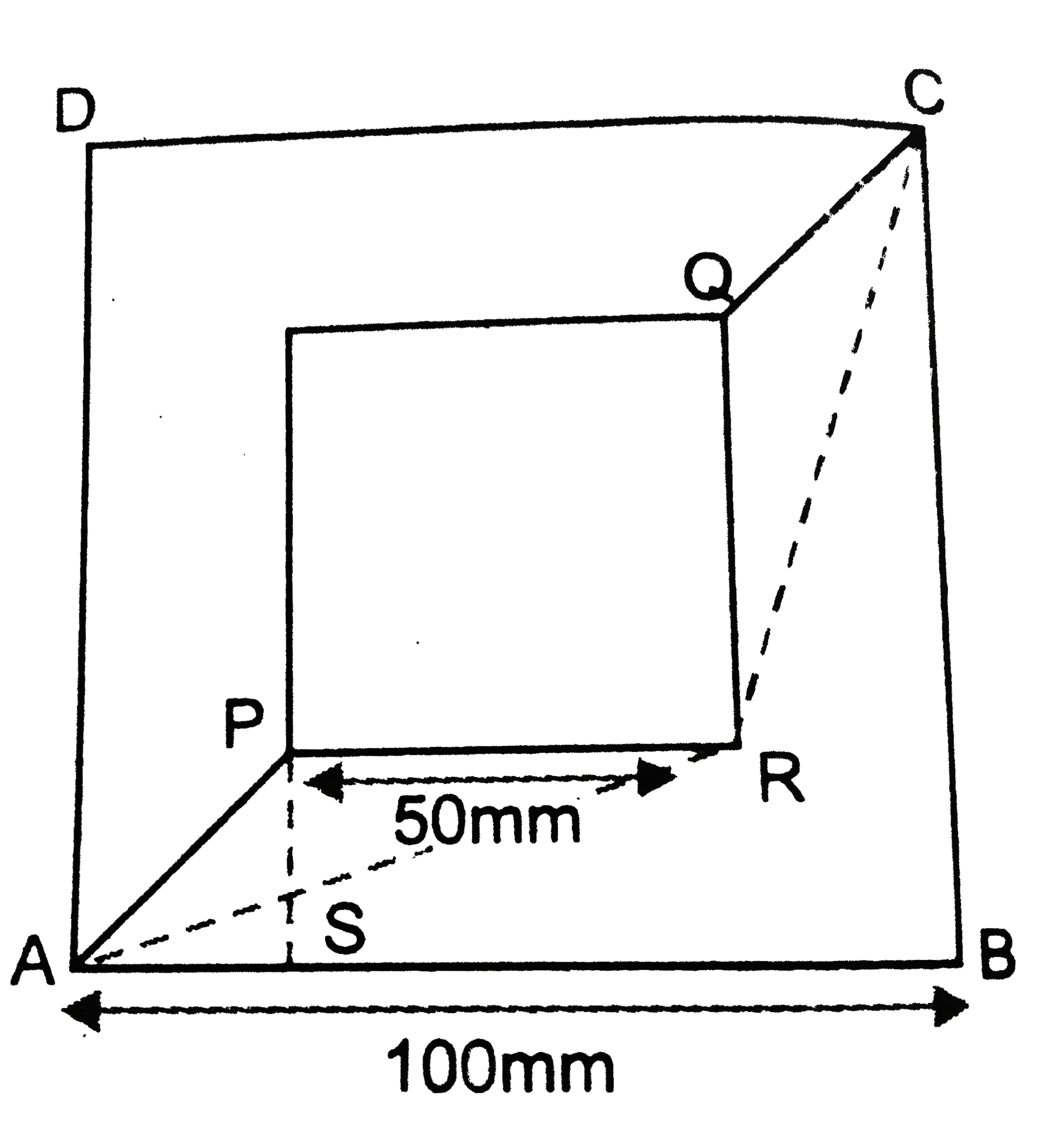
A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of 50m×50m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s (v<1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?
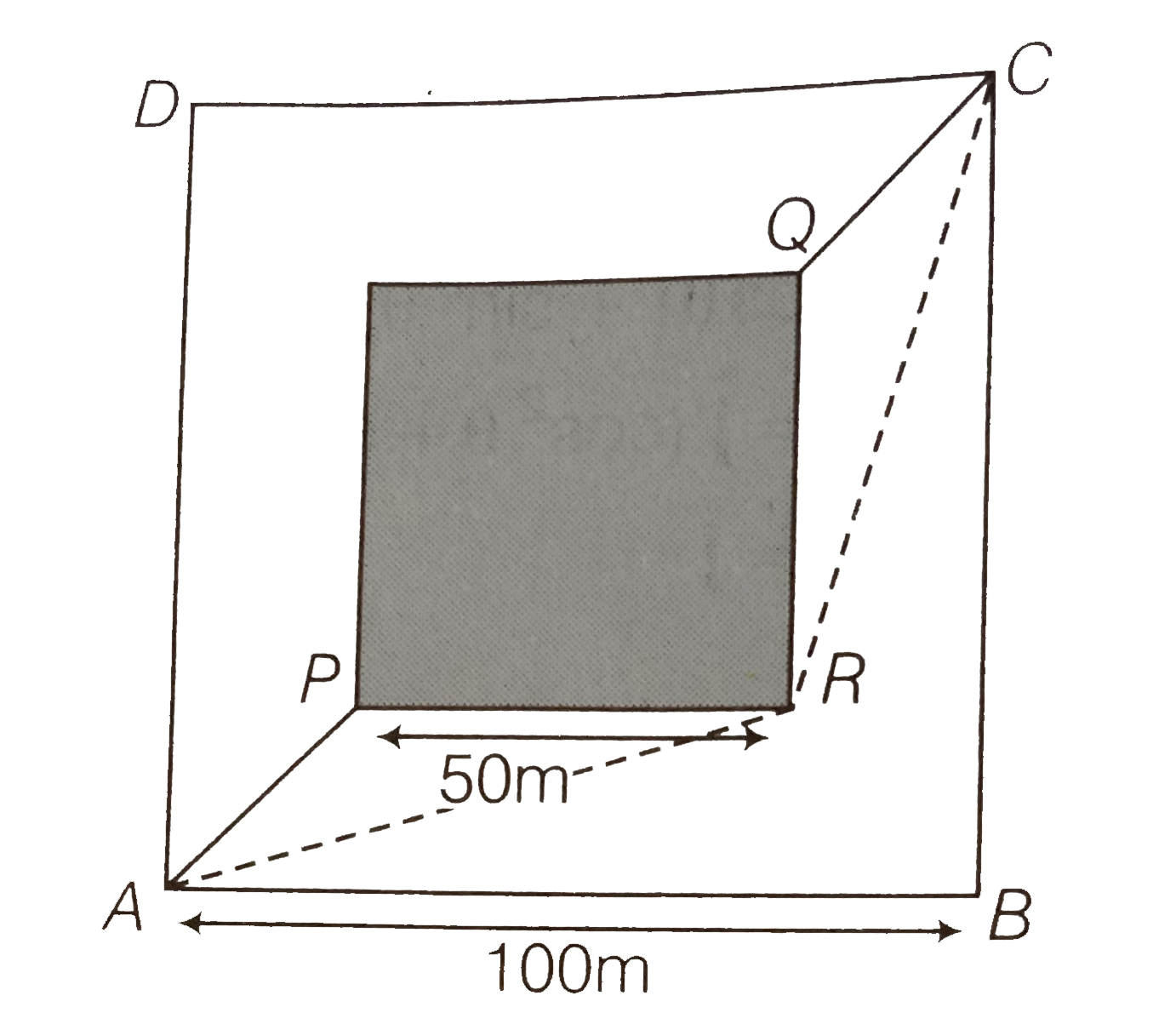
In Fig, 2 (EF) , 35, AR=√AT2+TR2=√752+252)=25√10=RC
Total path =AR+RC=2AR=50√10m
Time soutside sand , T0ut)=(50√10m1m/s=50√10s
AP=QC=√AS2+sP2=√252+50√2m
In sand , Tsand=AP+QC1+PQv
=25√2+25√21+(5)√2)v=50√2[1+1v]
Since Tsand<Tout
:. 50√2(1=1v)<50√10
or √2(1+1v)<√10 or (1+1v)<√10√2=√5 or 1v<√5−1or vlt 1/(sqrt 5-1) ~~ 0.81 m//s.
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:Advanced Problems
Explore 20 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:NCRT Exercises
Explore 22 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:5 Long answer (NCERT)
Explore 4 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of 50m×50m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s (v<1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?

View SolutionThe perimeter of the square is 64m. then the side of the square is:
View Solution
Knowledge Check
IF the area of square is 25m2, then the side of the square is
A125B625C125D5The side of a square park is 100 m. Perimeter of the park is:
A1000 mB400 mC200 mD800 m
The area of a square is 42.25 m2:
Find the side of the square.
View SolutionWhat is the area of a square whose side is m cm?
View SolutionArea of a square plot is 2304m2. Find the side of the square plot.
View SolutionThe diagonal of a square field measures 50 m. The area of square field is
View SolutionThe area of a square plot is 100 m2. Then the value of its perimeter is____m.
View Solution______ squares of each side 1 m makes a square of side 5 km.
View Solution

