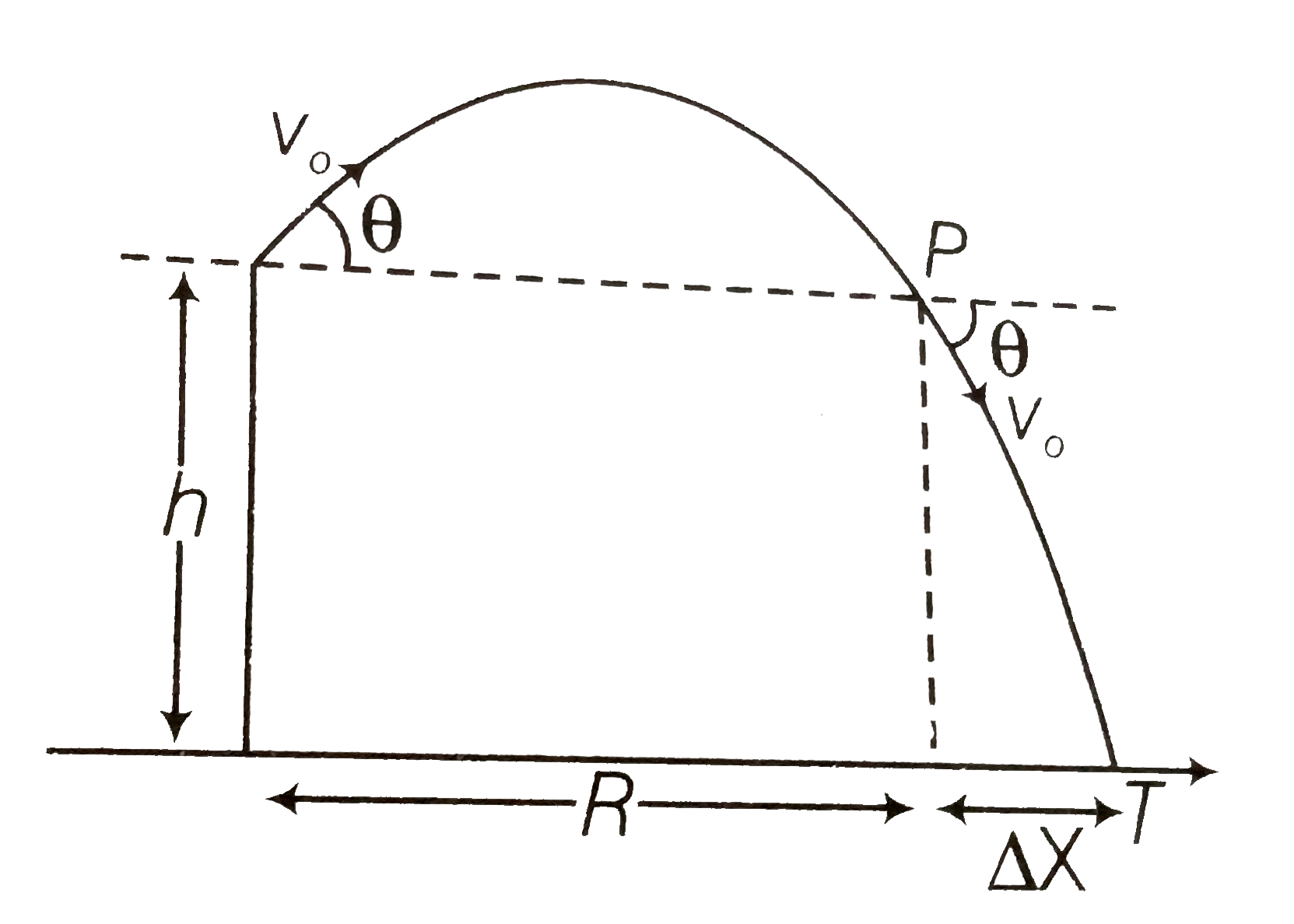
A gun can fire shells with maximum speed and the maximum horizontal range that can be achieved is . If a target farther away by distance (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least
![A gun can fire shells with maximum speed v(0) and the maximum horizontal range that can be achieved is R=(v(0)^(2))/(g). If a target farther away by distance Deltax (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least h=Delta x[1+(Deltax)/(R)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_NCERT_EXE_PHY_XI_C03_S01_030_Q01.png)
As per wuestion, the maximu , bborizontal range on ground is
It is if . The shell fired at (0) from height (h) can hit the same target at B. Fig. 2 ( EF). 25
as,
:.
(R+ Delta x) =0 + v) cos thea t t= ((R + delta x))./(v_0 cos theta) h=- v_0 sin theta xx (R + Delta x)/(v_0 cos theta) + 1/2 g ((R + Delta x^2)/(v_0^2 cos theat ) =- (R + Delat x) tan theta + 1/2 g ((R + Detal x)^2)/(v_0^2 cos theta^2 theta) theta = 45^@ h=- (R + Delta x) tan 45^@ + 1/2 (g(R+ Delta x)^2)/( 2 v_0^2 cos^@ 45^@ h=- (R + Delta x) xx 1 + 1/2 (g(R+ Delta x)^2)/v_0^2 [:. v_0^2 //g = R] =- (R + Delta x) + R + 2 Delta x + Delta x^2 //R = Delta x + Delta x^2 //R = Delta x (1 + Delta x//R).

Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:Advanced Problems
Explore 20 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:NCRT Exercises
Explore 22 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:5 Long answer (NCERT)
Explore 4 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R=v20g. If a target farther away by distance Δx (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least h=Δx[1+ΔxR]
View SolutionA gun can shoot a bullet upto a maximum horizontal range R .If the target is at a horizontal distance √3R2, at what elevation angle the gun should be held to hit the target?
View Solution
Knowledge Check
If the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
Acos−1(V2Rg)Bcos−1(gRV2)C12(V2Rg)D12sin−1(gRV2)
A particle is thrown with an initial speed v0 at an angle α to the horizontal. Find the radius of curvature r at the highest point of its path, and its ratios to the maximum height H and to the distance L of the particle's flight.
View SolutionA particle of mass m is fired vertically upward with speed v0(v0< escape speed ) . Prove that
(i) Maximum height attained by the particle is H=v20R2gR−v20 , where g is the acceleration due to gravity at the Earth's surface and R is the Earth's radius .
(ii) When the particel is at height h , the increase in gravitational potential energy is mgh1+hR
View SolutionA car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
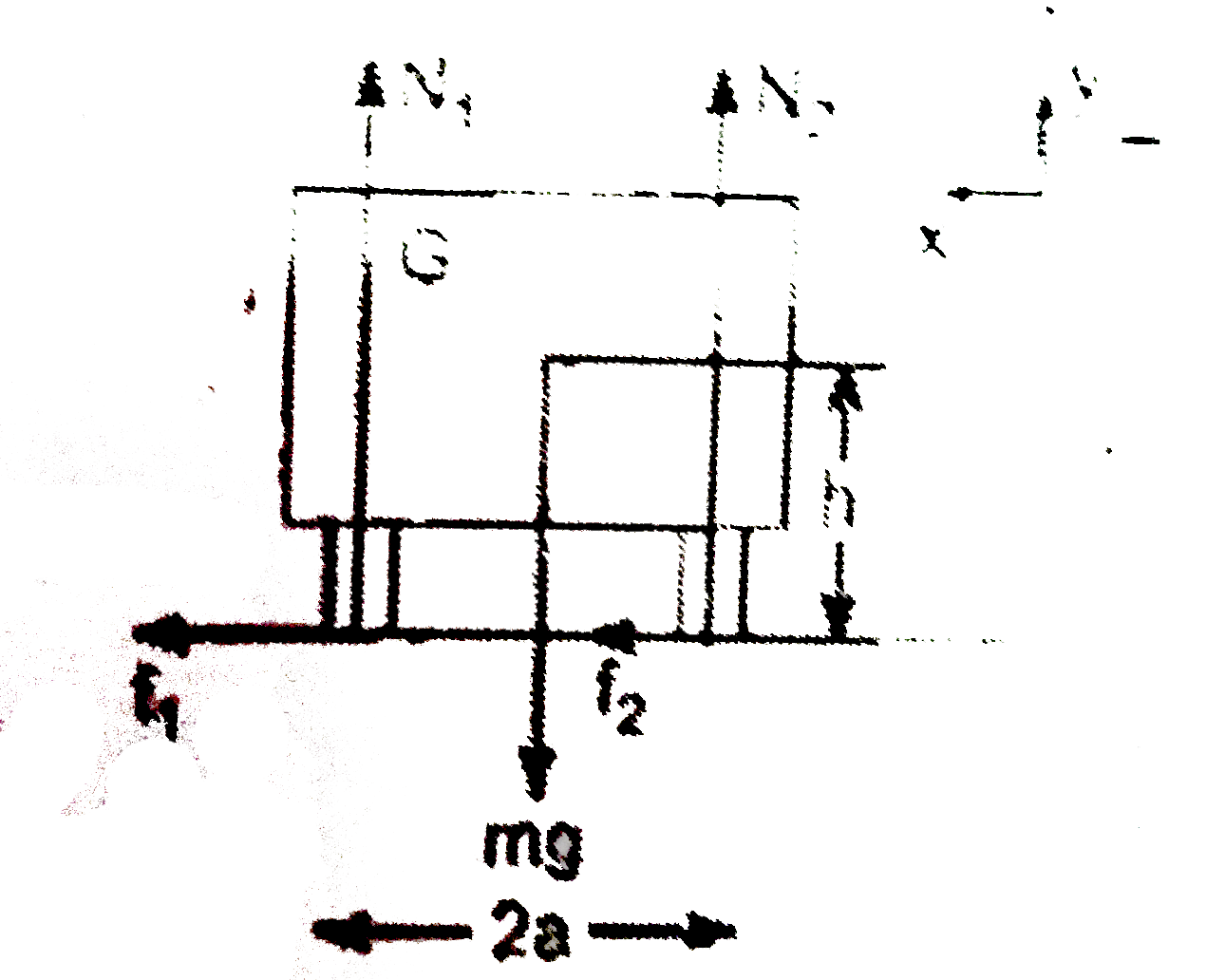
View SolutionAn artillery piece which consistently shoots its shells with the same muzzle speed has a maximum range R. To hit a target which is R/2 from the gun and on the same level, the elevation angle of the gun should be
View SolutionAn artillery piece which consistently shoots its shells with the same muzzle speed has a maximum range R. To hit a target which is R/2 from the gun and on the same level, the elevation angle of the gun should be
View SolutionAn artillary piece which consistently shoots its shells with the same muzzle speed has a maximum range R. To hit a target which is R/2 from the gun and on the same level, the elevation angle of the gun should be
View SolutionA jet plane files horizonally at a height h at a speed v. An anti-aircraft gun fires a shell at the plane when it is
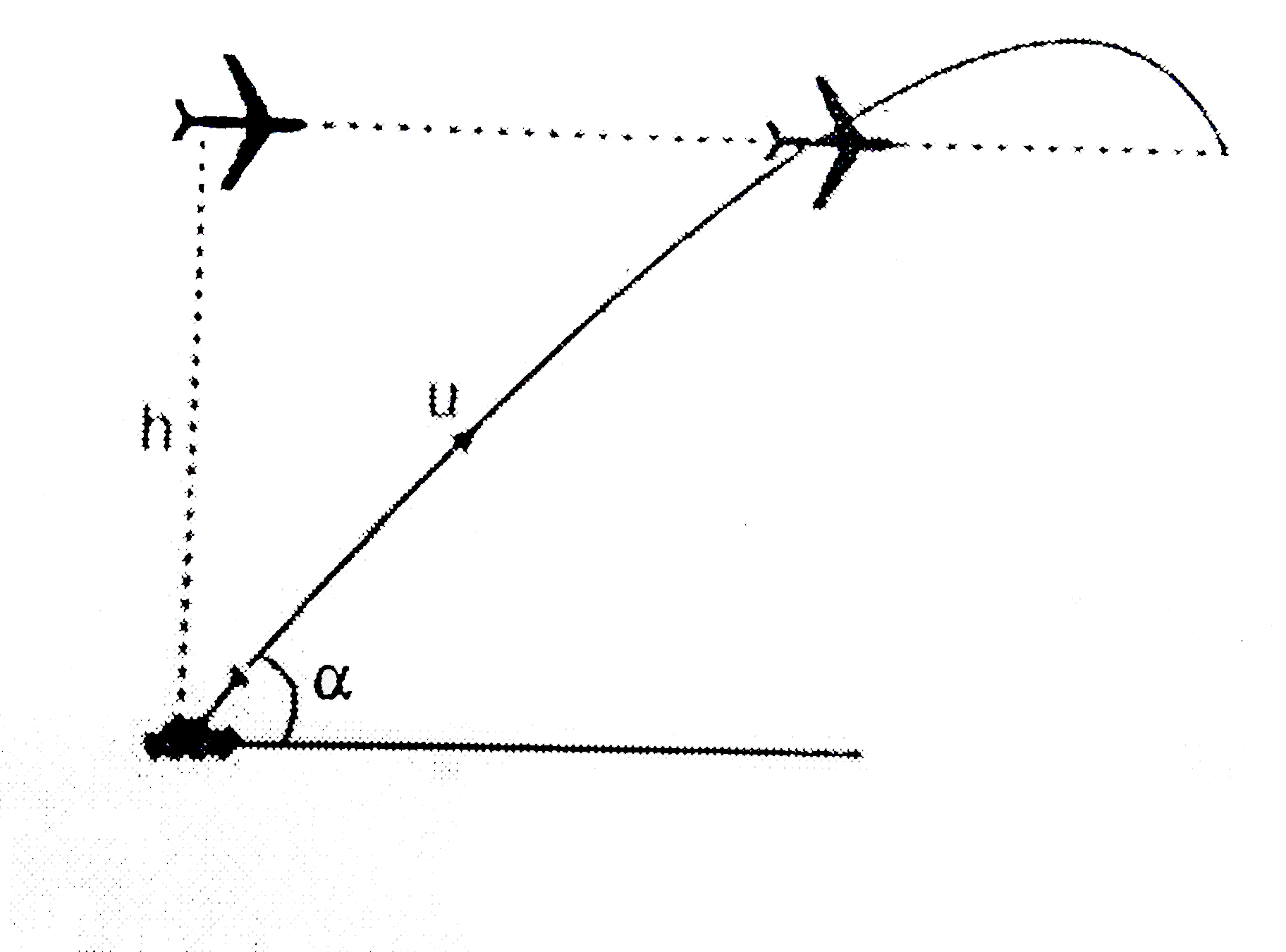
vertically above the gun. Show that the minimum muzzle speed required to hit the plane is √v2+2gh at an angle tan−1√2ghv
View Solution

