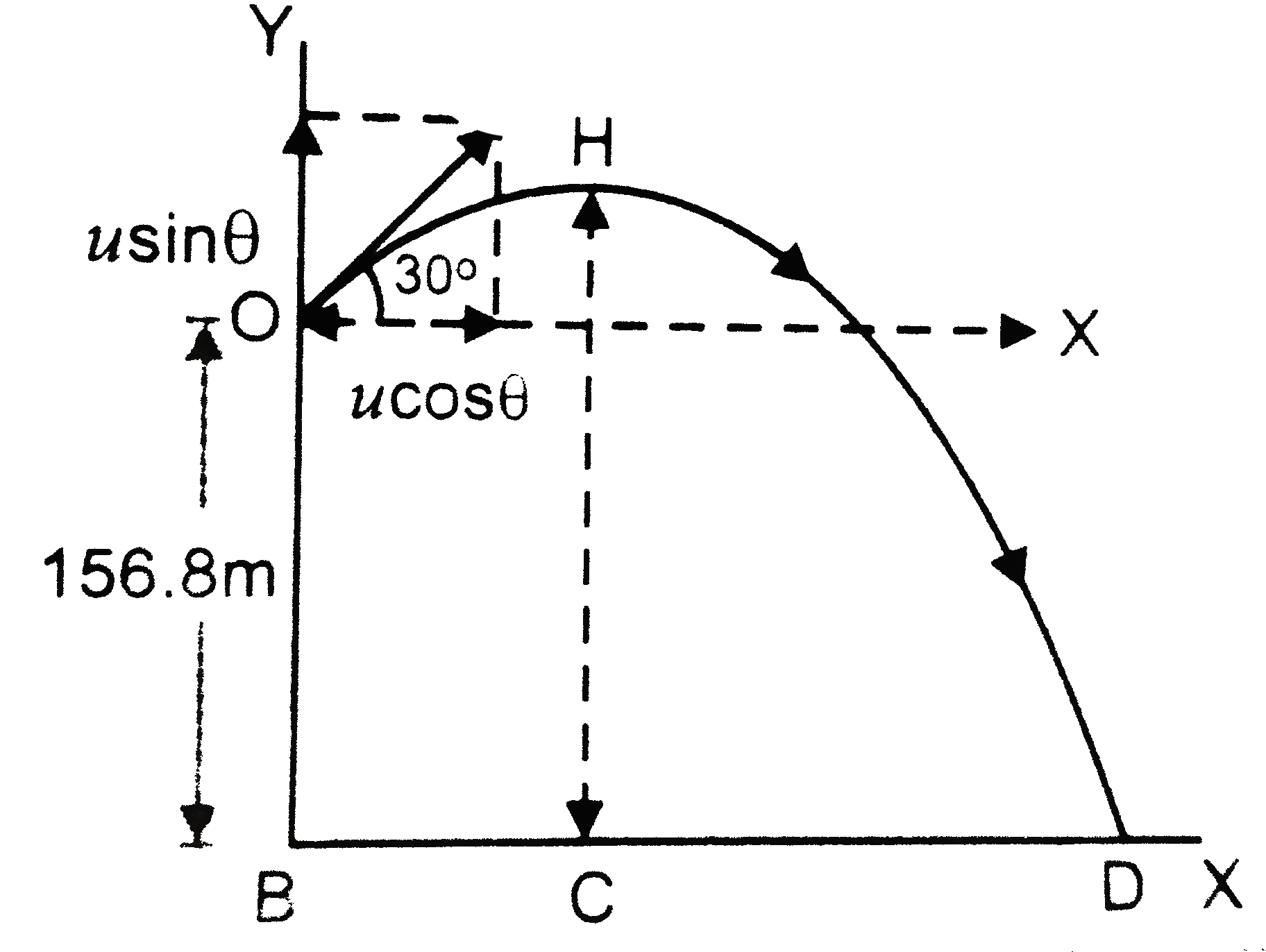
For the top of a tower $156.8 m$ high, a projectile is thrown up with a velcity of $39.2 m s^{- 1}$ , makingan angle $30 % (\circ)$ with borizontal direction. Find the distance from the foot of tower wher it strikes the ground and the time taken byit do so.

Video Solution

Text Solution

Verified by Experts

If Fig. 2(d). 26, height tower
$O B = 156.8 m, u = 39.2 m / s, θ = 30^{\circ}$
Component of velocity along $O X$
$= u cos θ = 30^{\circ} .2 {cos 30}^{\circ} = 33.947 m^{- 10}$
.
Component of velocity along $O Y$
$= u sin θ = 39 .2 {sin 30}^{\circ} = 19.6 m s^{- 1}$
Let (t) be the total time of flight (i.e time in going from $O \to D) . C o n s r t h e v e r t i c a l d o w n w a r d d i r e c t i o n$ OB $a s t h e p o s i t i v e d i r e c t i o n o f y - a ξ s . T a k \in g m o t i o n o f a p r o j e c t i \leq o m$ O to D $a l o n g Y - a ξ s, w e h a v e $ y_(0) =0, y= 156.8 m $, $ u_(y) =- sin 30^(@) =- 19.6 m//s $, $ a_(y) =9.8 m//s^(2) , t=t $ A s, y = y_{0} + u_{y} t + \frac{1}{2_{Y}} T^{2}$ ltBRgt :. 156. 8 =0 + (-19.6) t+ 1/2 xx 9.8 xx t^(2) $ or 156.8 = - 19.6 + 4.9 t^{2}$
or $4.9 t^{2} - 19.6 t 156.8 = 0$
or $t^{2} - 4 t - 32 = 0$
or $t^{2} - 8 t + 4 t - 32 = 0$
or $t (t - 8) + 4 (t - 8) = 0$
or $(t - 4) (t - 8) = 0 or t = - 4 or 8$ .
As $t = - 4 s i s \neg p o s s i b \leq ∴$ t=8 s $ D i s tan c e o m t h e f \infty t o f \to w e r w h e r i t s t r i k e s t h e g r o u n d i s$
$B D = u {cos 30}^{\circ} \times t = 33.947 \times = 271.57 m$ .

Updated on:21/07/2023

A ball is thrown from the top of tower with an initial velocity of $10 m s^{- 1}$ at an angle of $30^{\circ}$ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is $(T a k e g = 10 m s^{- 2})$
A $5 m$
B $20 m$
C $15 m$
D $10 m$
From the top of a tower of height 40m, a ball is projected upward with a speed of $20 m s^{- 1}$ at an angle of elevation of $30^{\circ}$ . Then the ratio of the total time taken by the ball to hit the ground to the time taken to ball come at same level as top of tower.
A $2 : 1$
B $3 : 1$
C $3 : 2$
D $4 : 1$
From the top of a tower, 80m high from the ground a stone is thrown in the horizontal direction with a velocity of $8 m s^{1}$ . The stone reaches the ground after a time t and falls at a distance of d from the foot of the tower. Assuming $g = 10 m s^{2}$ , the time t and distance d are given respectively by
A6s,64m
B6s,48m
C4s,32m
D4s,16m