A particle moves along a circle of radius R. It starts from (A) and moves in antilockwise direction. Calculate the distance travelled by particle (a)one complete revolution. Also calcuate the magnituede of displacement in each case. Fig. 2 (a) .28.
Let's solve the problem step by step:
(a) Distance Travelled and Displacement for One Complete Revolution
1. Distance Travelled:
- When a particle completes one full revolution around a circle of radius R, it travels the circumference of the circle.
- The circumference C of a circle is given by:
C=2πR
- Therefore, the distance travelled by the particle in one complete revolution is:
Distance=2πR
2. Displacement:
- Displacement is the shortest distance between the initial and final positions of the particle.
- For one complete revolution, the particle returns to its starting point.
- Therefore, the displacement is:
Displacement=0
Summary:
- Distance Travelled in One Complete Revolution: 2πR
- Displacement in One Complete Revolution: 0
- When a particle completes one full revolution around a circle of radius R, it travels the circumference of the circle.
- The circumference C of a circle is given by:
C=2πR
- Therefore, the distance travelled by the particle in one complete revolution is:
Distance=2πR
- Displacement is the shortest distance between the initial and final positions of the particle.
- For one complete revolution, the particle returns to its starting point.
- Therefore, the displacement is:
Displacement=0
- Distance Travelled in One Complete Revolution: 2πR
- Displacement in One Complete Revolution: 0
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 SolvedExamples
Explore 31 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:3 SolvedExamples
Explore 46 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
In Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves from A to C
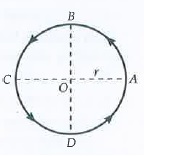
View SolutionIn Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves from A to B

View Solution
Knowledge Check
A particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
Adistance travelledBdisplacementCaverage speedDaverage velocityA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsin.ωt2A particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsinωt2
In Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves A to D
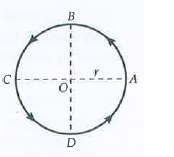
View SolutionAB is diameter of circle of radius r. A particle starting from A completes two and half revolution. Calculate the distance travelled by the particle and its displacement

View SolutionA particle is moving along a circular track of radius r. What is the distance traversed by particle in half revolution ? What is its displacement ?
View SolutionA particle moves on a circular path of radius 'r'. It completes one revolution in 40s. Calculate distances displacement in 2 min 20 s.
View SolutionA particle is moving in a circle of diameter 5m. Calculate the distance covered and the displacement when it completes 3 revolutions.
View Solution

