Compare the power used in the 2Ω resistor in each of the following circuits :
(i) a 6V battery in series with 1Ωand2Ω resistors, and
(ii) a 4V battery in parallel with 12Ωand2Ω resistors.
P1/P2 = 2
P1/P2 = 3
P1/P2 = 1
None
The correct Answer is:C
To solve the problem, we need to calculate the power used in the 2Ω resistor for both circuits separately and then compare them.
Part (i): Series Circuit with a 6V Battery
1. Identify the Total Resistance:
- The resistors are in series: 1Ω and 2Ω.
- Total resistance \( R_{\text{eq}} = R_1 + R_2 = 1 Ω + 2 Ω = 3 Ω \).
2. Calculate the Current:
- Using Ohm's Law, the total current \( I \) in the circuit can be calculated using the formula:
\(
I = \frac{V}{R_{\text{eq}}}
\)
- Substituting the values:
\(
I = \frac{6V}{3Ω} = 2 A
\)
3. Calculate the Power in the 2 Ω Resistor:
- The power \( P \) across the 2Ω resistor can be calculated using the formula:
\(
P = I^2 \times R
\)
- Substituting the values:
\(
P = (2 A)^2 \times 2 Ω = 4 \times 2 = 8 W
\)
Part (ii): Parallel Circuit with a 4V Battery
1. Identify the Voltage across the 2 Ω Resistor:
- In a parallel circuit, the voltage across each resistor is the same as the voltage of the battery.
- Therefore, the voltage across the 2Ω resistor is 4V.
2. Calculate the Power in the 2 Ω Resistor:
- The power \( P \) across the 2Ω resistor can be calculated using the formula:
\(
P = \frac{V^2}{R}
\)
- Substituting the values:
\(
P = \frac{(4V)^2}{2Ω} = \frac{16}{2} = 8 W
\)
Comparison of Power in Both Circuits
- In both cases, the power used in the 2Ω resistor is:
- Series Circuit: \( 8 W \)
- Parallel Circuit: \( 8 W \)
Thus, the power used in the 2Ω resistor is the same in both circuits.
Final Answer:
The power used in the 2Ω resistor in both circuits is equal, \( 8 W \).
---
- The resistors are in series: 1Ω and 2Ω.
- Total resistance \( R_{\text{eq}} = R_1 + R_2 = 1 Ω + 2 Ω = 3 Ω \).
- Using Ohm's Law, the total current \( I \) in the circuit can be calculated using the formula:
\(
I = \frac{V}{R_{\text{eq}}}
\)
- Substituting the values:
\(
I = \frac{6V}{3Ω} = 2 A
\)
- The power \( P \) across the 2Ω resistor can be calculated using the formula:
\(
P = I^2 \times R
\)
- Substituting the values:
\(
P = (2 A)^2 \times 2 Ω = 4 \times 2 = 8 W
\)
- In a parallel circuit, the voltage across each resistor is the same as the voltage of the battery.
- Therefore, the voltage across the 2Ω resistor is 4V.
- The power \( P \) across the 2Ω resistor can be calculated using the formula:
\(
P = \frac{V^2}{R}
\)
- Substituting the values:
\(
P = \frac{(4V)^2}{2Ω} = \frac{16}{2} = 8 W
\)
- In both cases, the power used in the 2Ω resistor is:
- Series Circuit: \( 8 W \)
- Parallel Circuit: \( 8 W \)
The power used in the 2Ω resistor in both circuits is equal, \( 8 W \).
Topper's Solved these Questions
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Exemplar)Short Answer
10 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Exemplar)Long Answer
6 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - NCERT Question
23 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test
21 Videos
Similar Questions
Compare the power used in the 2Ω resistor in each of the following circuits: (i) a 6V battery in series with 1Ωand2Ω resistors, and (ii) a 4V battery in parallel with 12Ωand2Ω resistors.
View SolutionCompare the power used in the 2Ω resistor in each of the following circuits:
(i) a 6 V battery in series with 1Ω and 2Ω resistors, and (ii) a 4 V battery in parallel with 12Ω and 2Ω resistors.
View Solution
Knowledge Check
If power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
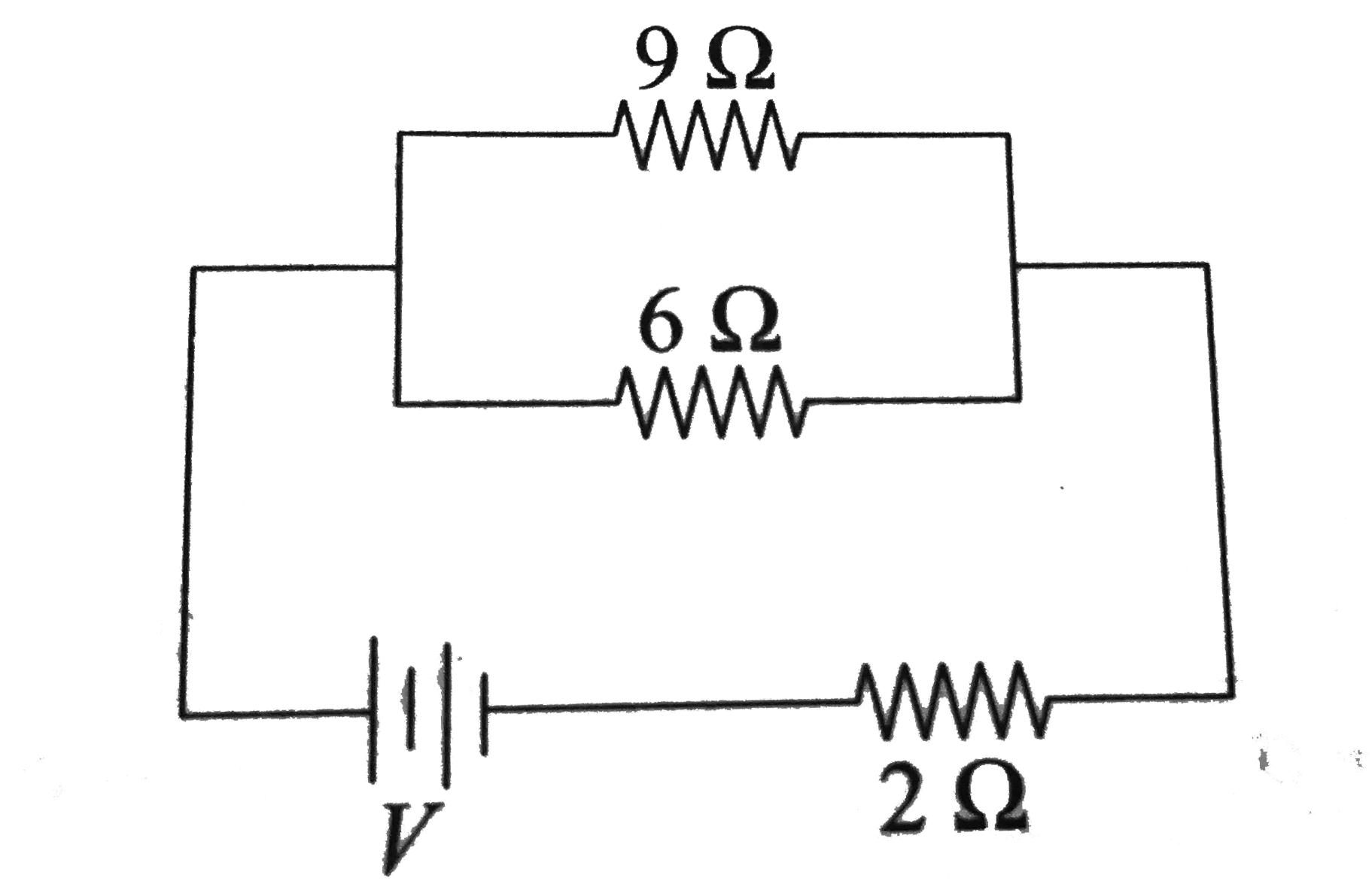 A8VB10VC2VD4V
A8VB10VC2VD4VThe power dissipated in 3Ω resistor in the circuits as shown in the figure is 2W. The power dissipated in 7Ω resistor will be
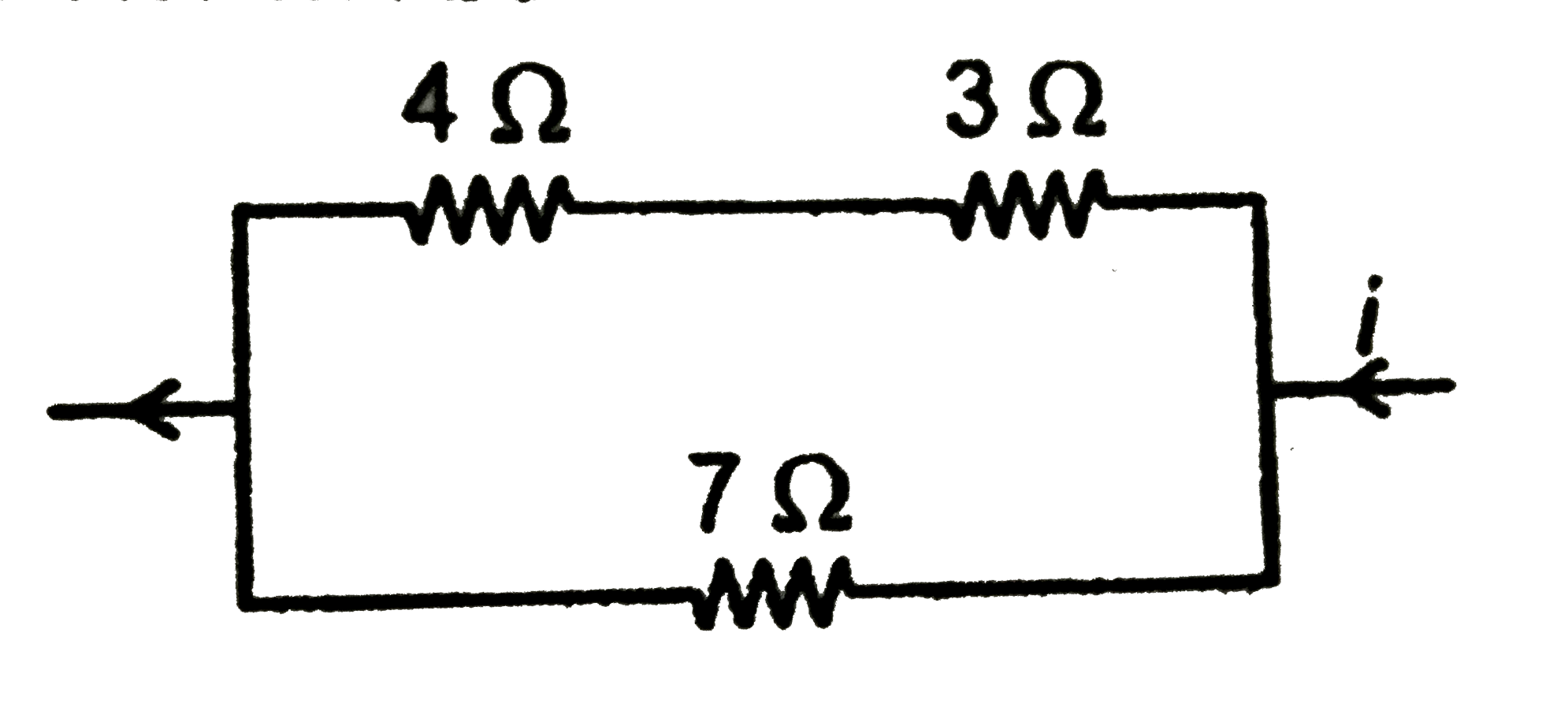 A14WB143WC73WD7W
A14WB143WC73WD7WTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
Asame current flowing through them when connected in parallelBsame current flowing through them when connected in seriesCsame potential difference across them when connected in seriesDdifferent potential differences across them when connected in parallel.
Compare the power used in the 2 ω resistor in each of the following circuits :
a 6 V battery in series with 1 ω and 2 ω resistors, and
View SolutionCompare the power used in the 2 ω resistor in each of the following circuits :
a 4 V battery in parallel with 12 ft and 2 ft resistors.
View SolutionIn the following circuit, the current drawn from the battery is 2A. If the 5Ω resistance is replaced by a 20Ω resistor, then the current drawn from the battery will be
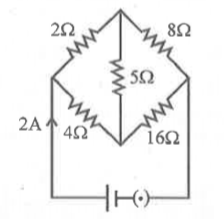
View Solution6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
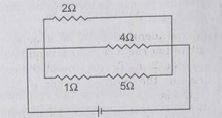
View Solution
