The velocity v of a particle of mass in moving along a straight line change within time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
The particle does not perform SHM
The particle perform SHMwith time period 2π√mk
The particle perform SHMwith time frequency√k2π
The particle perform SHMwith time period 2πK
The correct Answer is:C
d2vdt=−kv2
this equation has standard solution v=v0sin(√kt+θ)where =ω=√k
Hence the particle executes SHM with angular frequency ω=√k or frequency f=√k2π.
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Spring Particle System
Explore 24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Simple Pendulum And Different Cases Of Shm
Explore 25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
The acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of time
View Solution
Knowledge Check
The velocity v of a particle of mass in moving along a straight line change within time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
AThe particle does not perform SHMBThe particle perform SHMwith time period 2π√mkCThe particle perform SHMwith time frequency√k2πDThe particle perform SHMwith time period 2πKThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
Ais constantBis increasingCis decreasingDfirst increase and then decreases
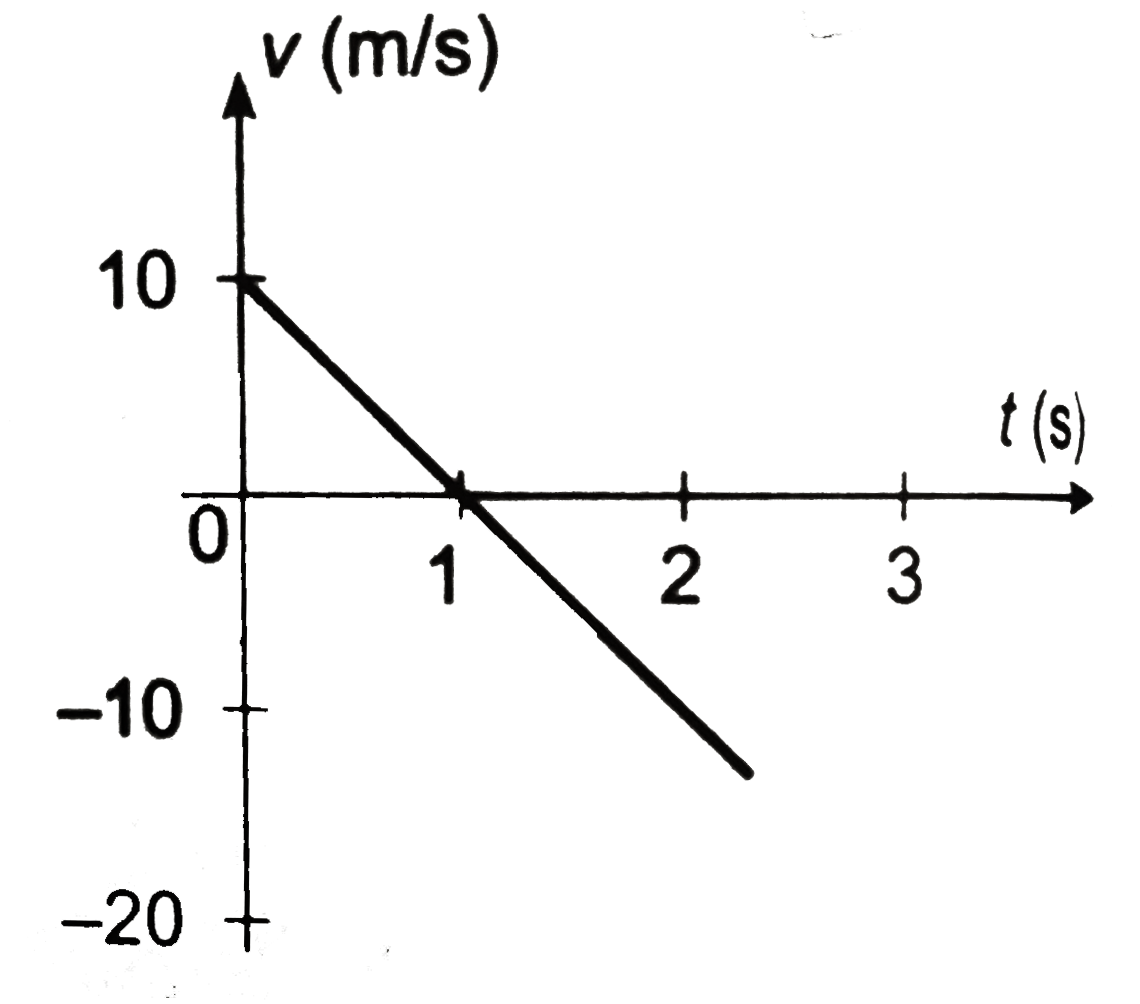
The figure shows velocity-time graph of a particle moving along a straight line. Identify the correct statement.
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionThe displacement x of a particle at time t moving along a straight line path is given by x2=at2+2bt+c where a, b and c are constants. The acceleration of the particle varies as
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View Solution

