The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of time
0.5sec
1sec
2sec
None of these
The correct Answer is:B
The velocity of particle changes sign at t=1sec.
∴ Distance from t=0 to t=2sec.is =0∫1vdt+1∫2vdt
=[(t3−32t2)]00+[(t3−32t2)]12=3m
Displacement from t=0 to t=2sec. is 2∫0vdt
=[(t3−32t2)]20=2m.
Similar Questions
The speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=(3t2+5t) where t is in second and v is in m/s. Find the resultant acceleration at t = 1s.
View Solution
Knowledge Check
The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :A1mB2mC3mD4mThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :A2mB3mC4mD6mThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)
Velocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
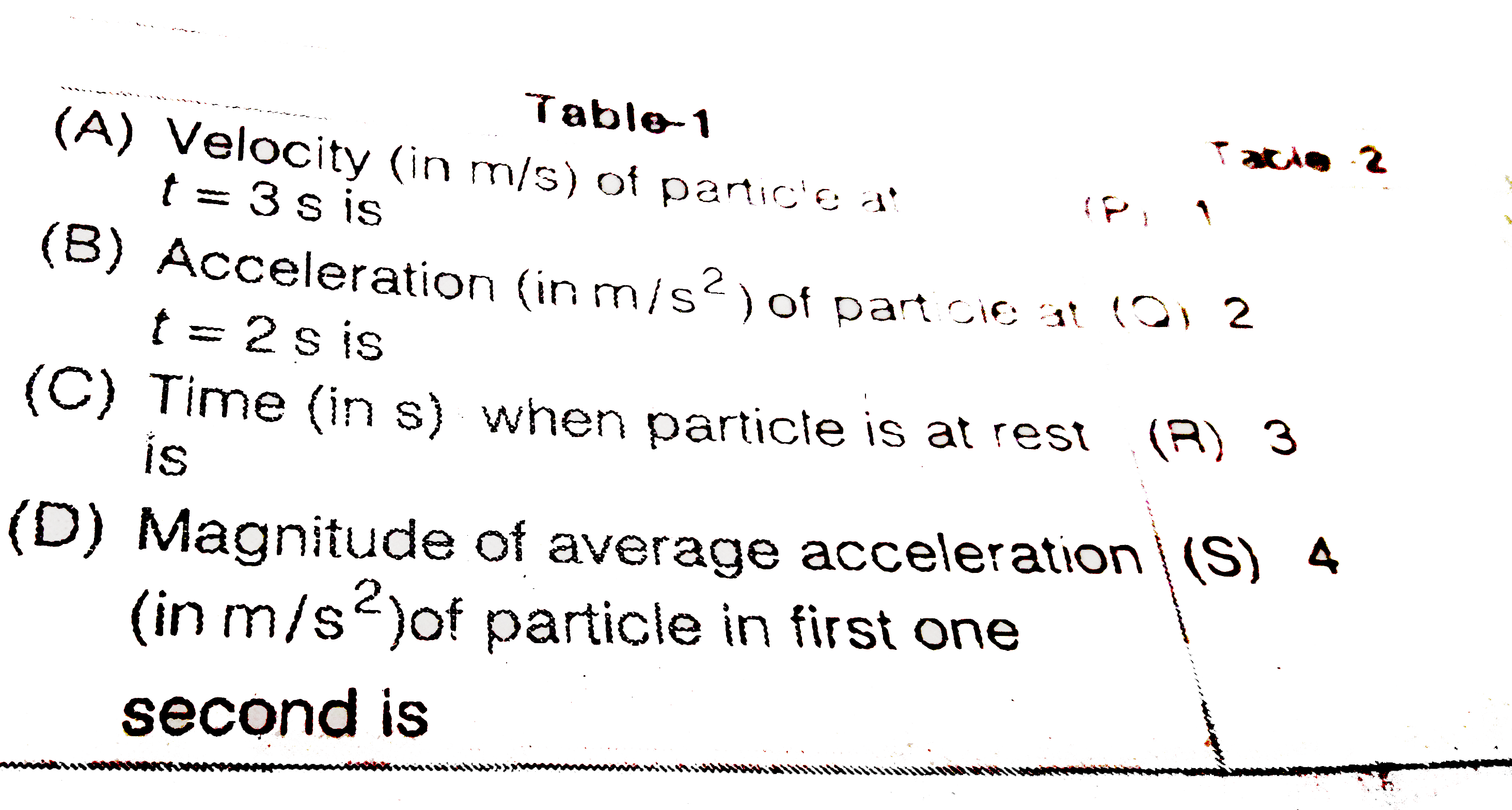
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionVelocity of a particle moving in a curvilinear path varies with time as v=(2tˆi+t2ˆk)m/s. Here t is in second. At t=1 s
View SolutionThe velocity of an object moving rectillinearly is given as a functiion of time by v=4t−3t2 where v is in m/s and t is in seconds. The average velociy if particle between t=0 to t=2 seconds is
View SolutionA particle moves in a circle of radius 20cm. Its linear speed is given by v=2t where t is in seconds and v in ms−1. Then
View Solution