The potential energy of interaction between the semi-circular ring of mass M and radius R, and the particle of mass M placed at the centre of curvature of the semi-circular arc is:
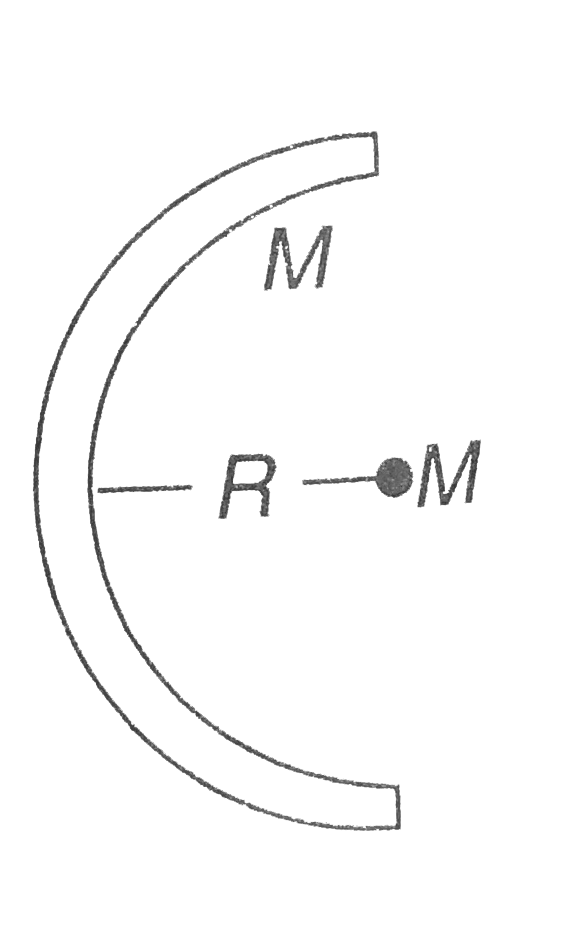
A
−GM2R
B
−2GM2R
C
−GM2πR
D
none of these
Video Solution
Text Solution
The correct Answer is:A
v=−GMMR=−GM2R
|
Topper's Solved these Questions
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Motion Of Satellite
Explore 33 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Problems Based On Mixed Concepts
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Gravitational Field And Acceleration Due To Gravity
Explore 34 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRThe total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
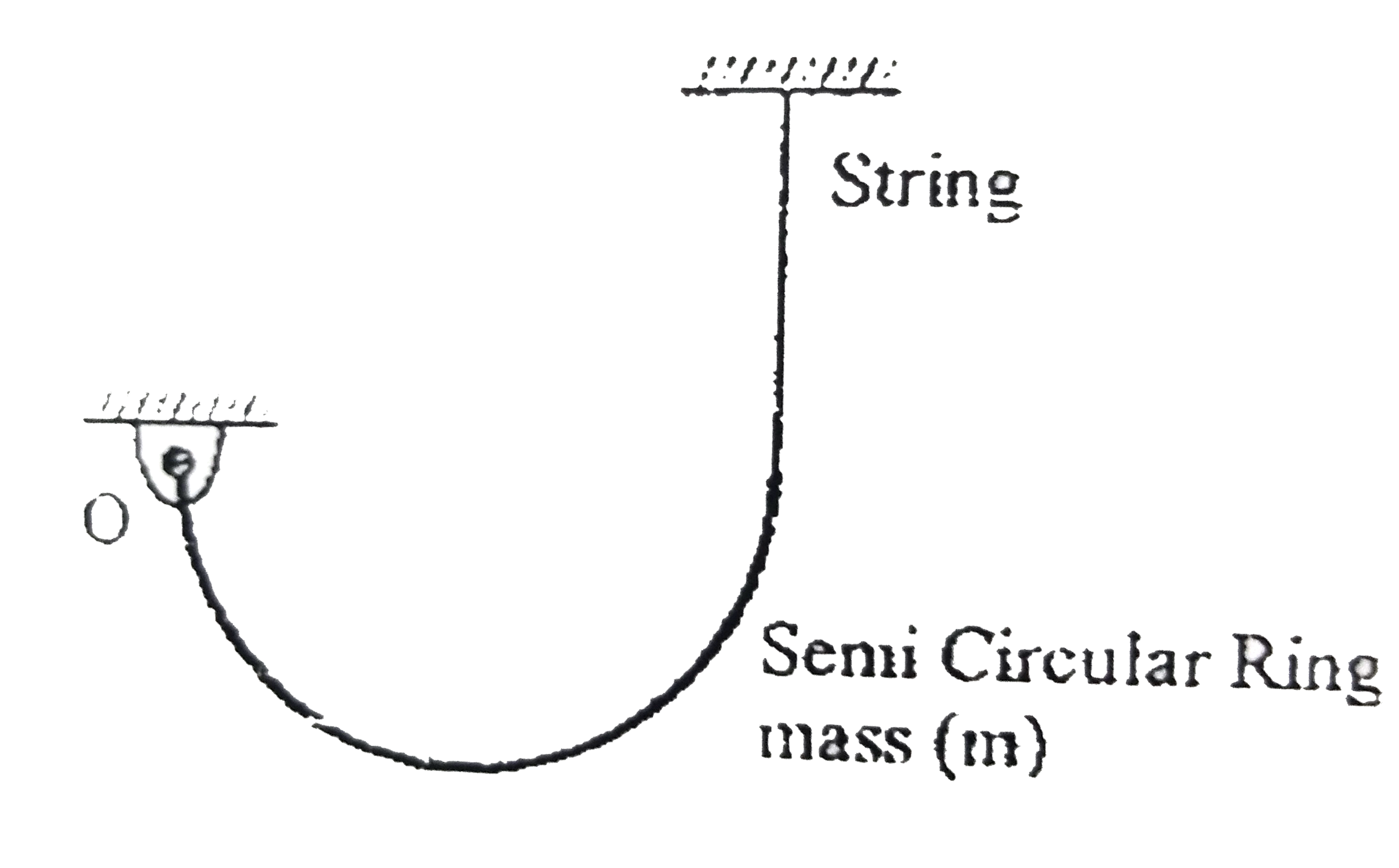 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
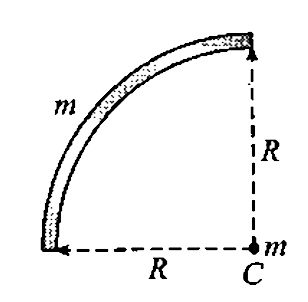
View SolutionThe coordinates of centre of mass of the following quarter circular arc is -

View Solution

