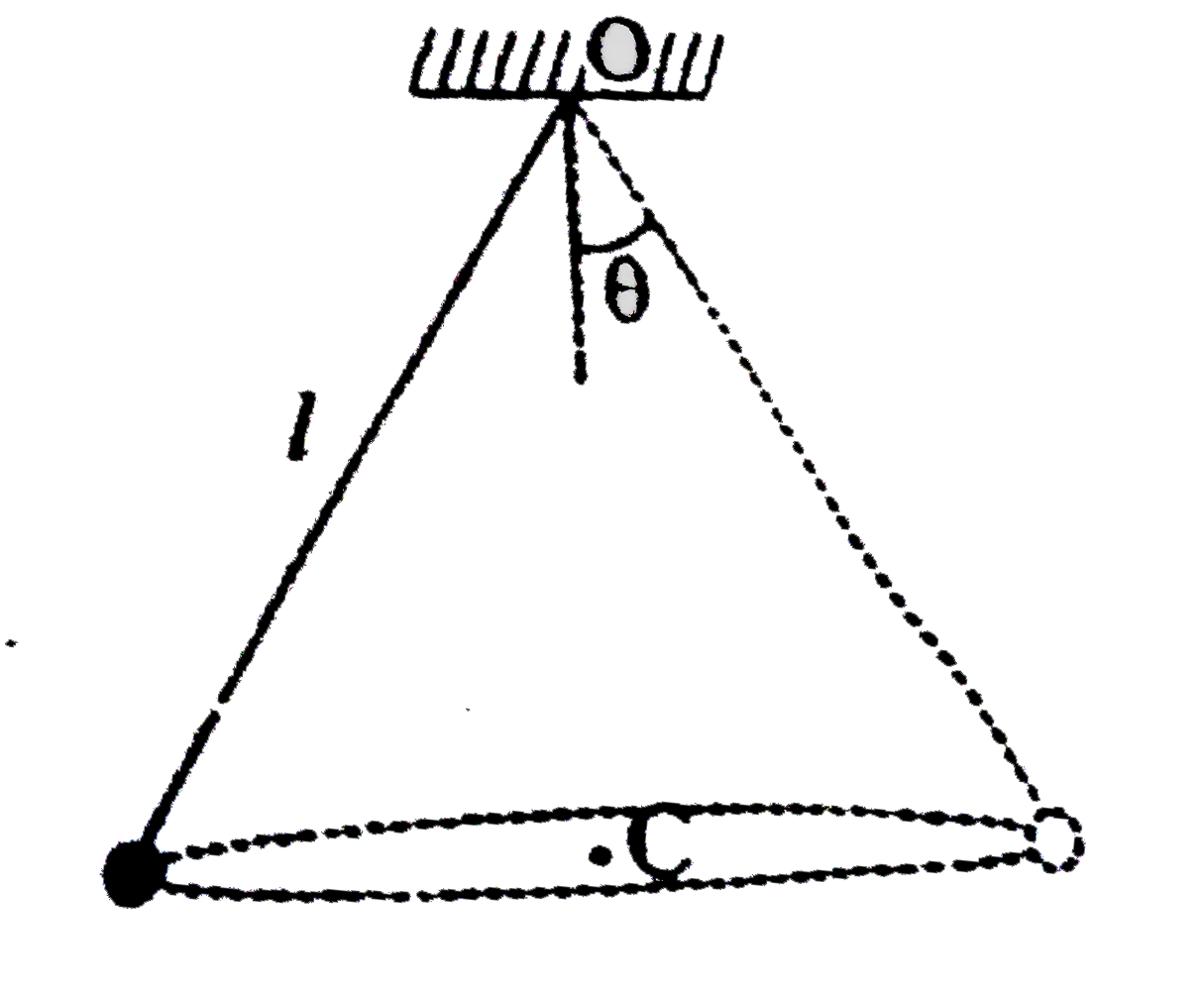
A conical pendulum consists of a bob of mass m in motion in a circular path in a horizontal plane as shown in figure. During the motion, the supporting wire of length l. Maintains a constant angle θ with the vertical. The magnitude of the angular momentum of the bob about the vertical dashed line is.
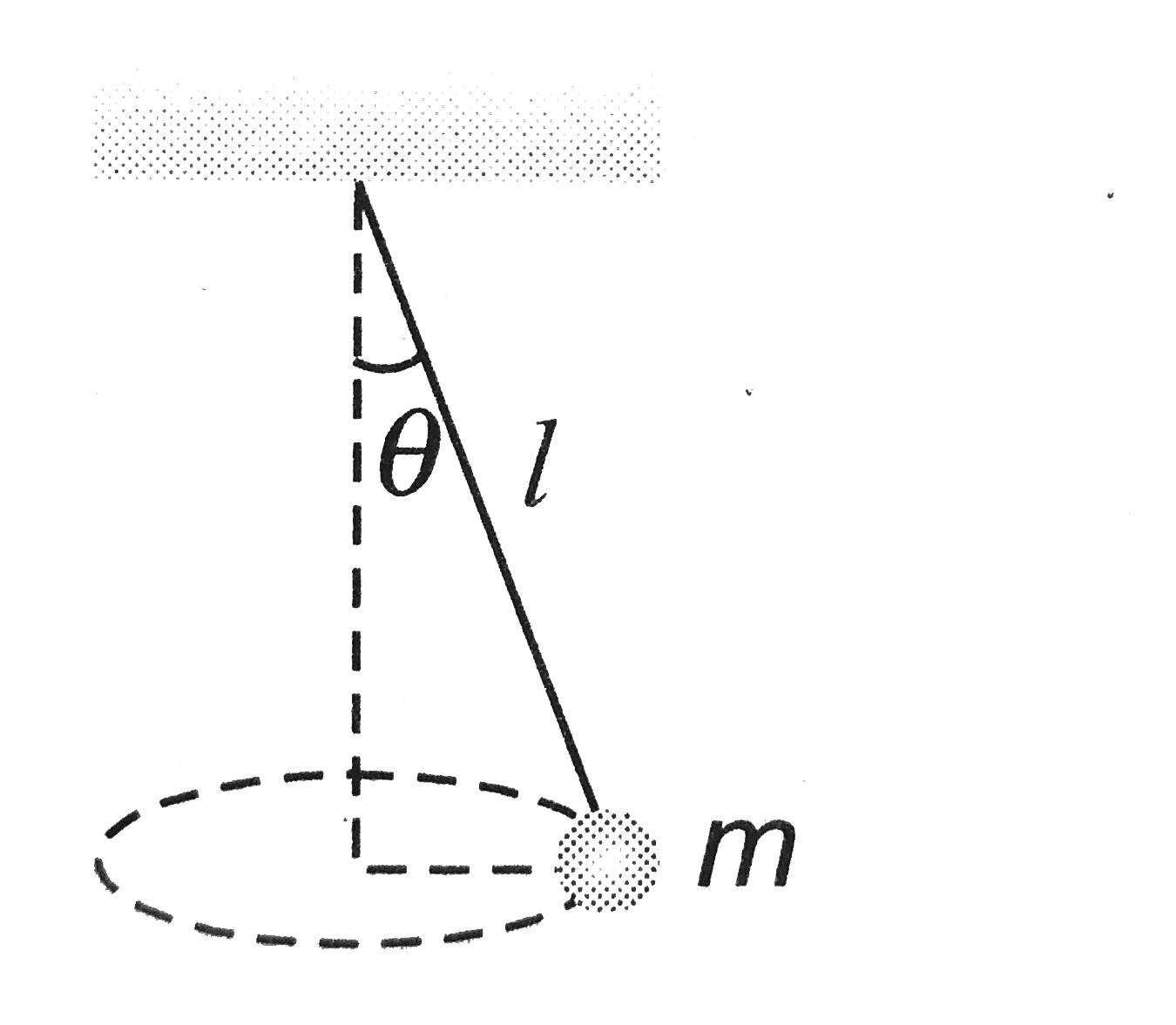 .
.
(m2gl3cos4θsinθ)1/2
(m2gl3cos4θcosθ)1/2
(m2gl3sin3θcosθ)1/2
(m2gl3cos3θcosθ)1/2.
The correct Answer is:B
(b) We start with the particle under a net force model in the x and y directions :
∑Fx=max:Tsinθ=mv2r
∑Fy=may:Tcosθ=mg
So sinθcosθ=v2rg and v=√rg(sinθcosθ)
then L=rmvsin90∘=rm√rg(sinθcosθ)=√m2gr3sinθcosθ
and since r=lsinθ,
L=√m2gl3sin4θcosθ.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Work And Energy In Case Of Rotation
Explore 22 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Torque , Torque Equation And Equilibrium Of A Rigid Body
Explore 29 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A simple pendulum of length l ils pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weitht w of the bob about the point of suspension. When is the torque zero?
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
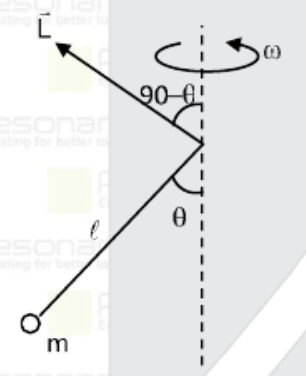
View Solution
Knowledge Check
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
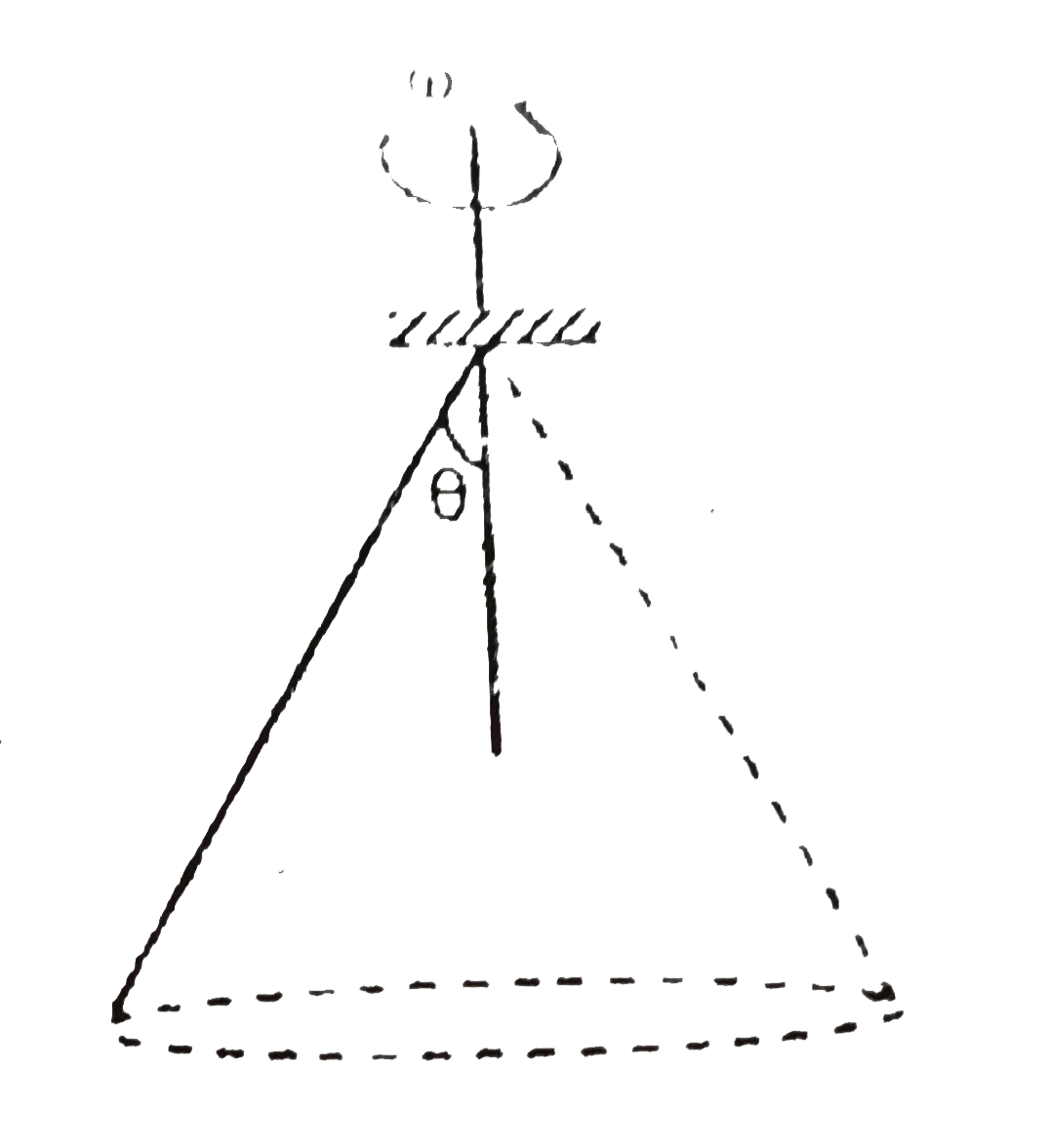 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6A conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
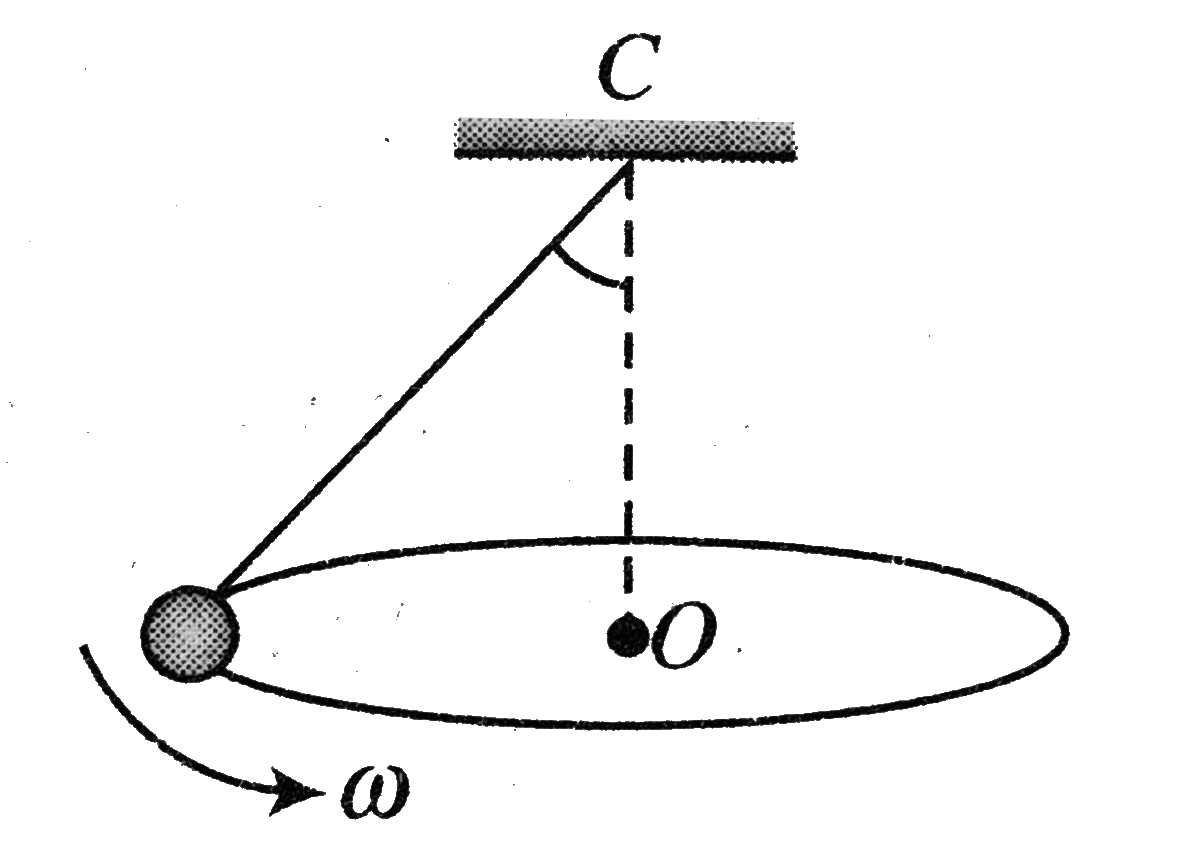 A→L is constantBonly direction of →L is constantConly magnitude of →L is constantDnone of the above
A→L is constantBonly direction of →L is constantConly magnitude of →L is constantDnone of the aboveA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
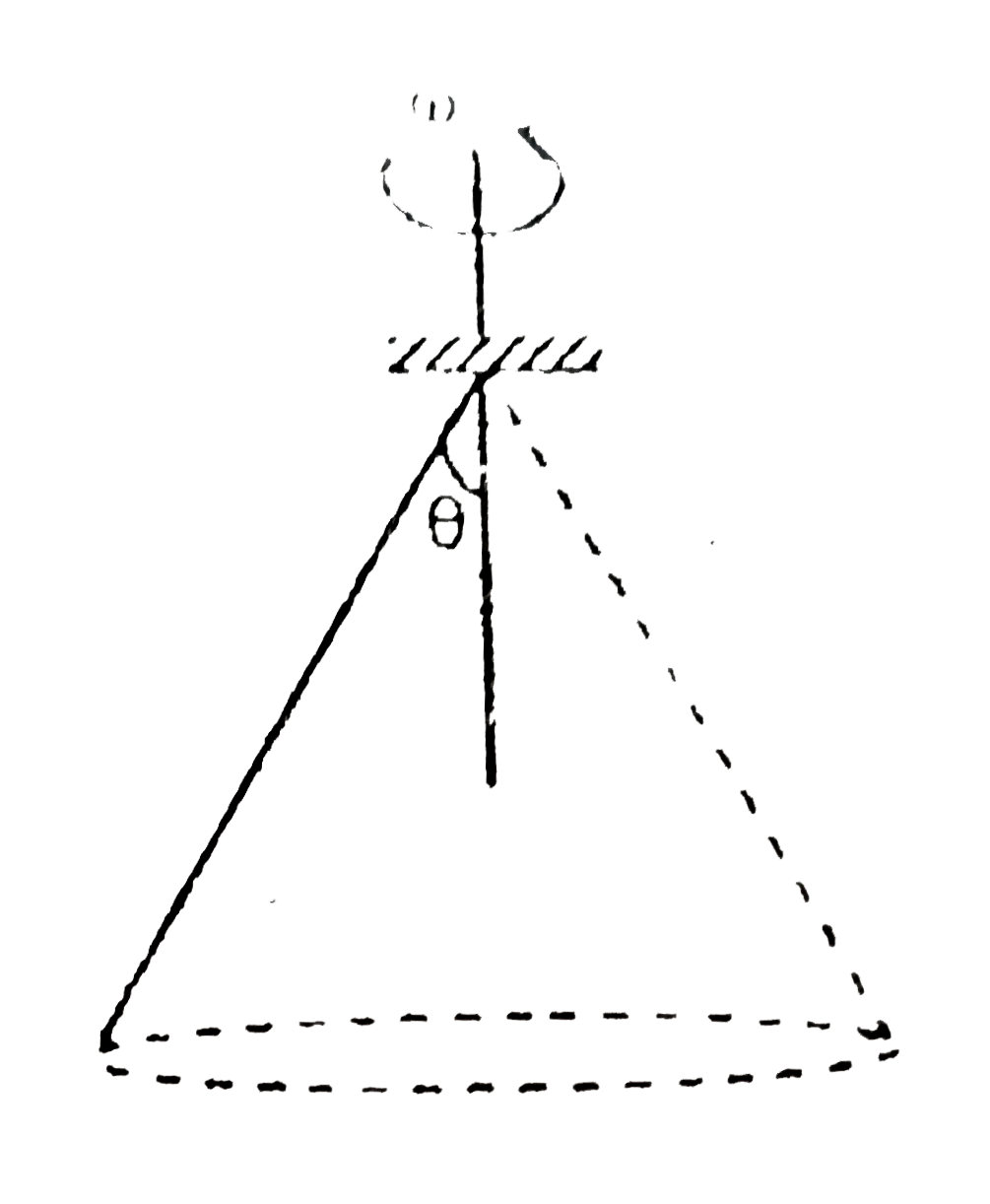 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulu) as shown in the figure. If speed of the particle is constant then,
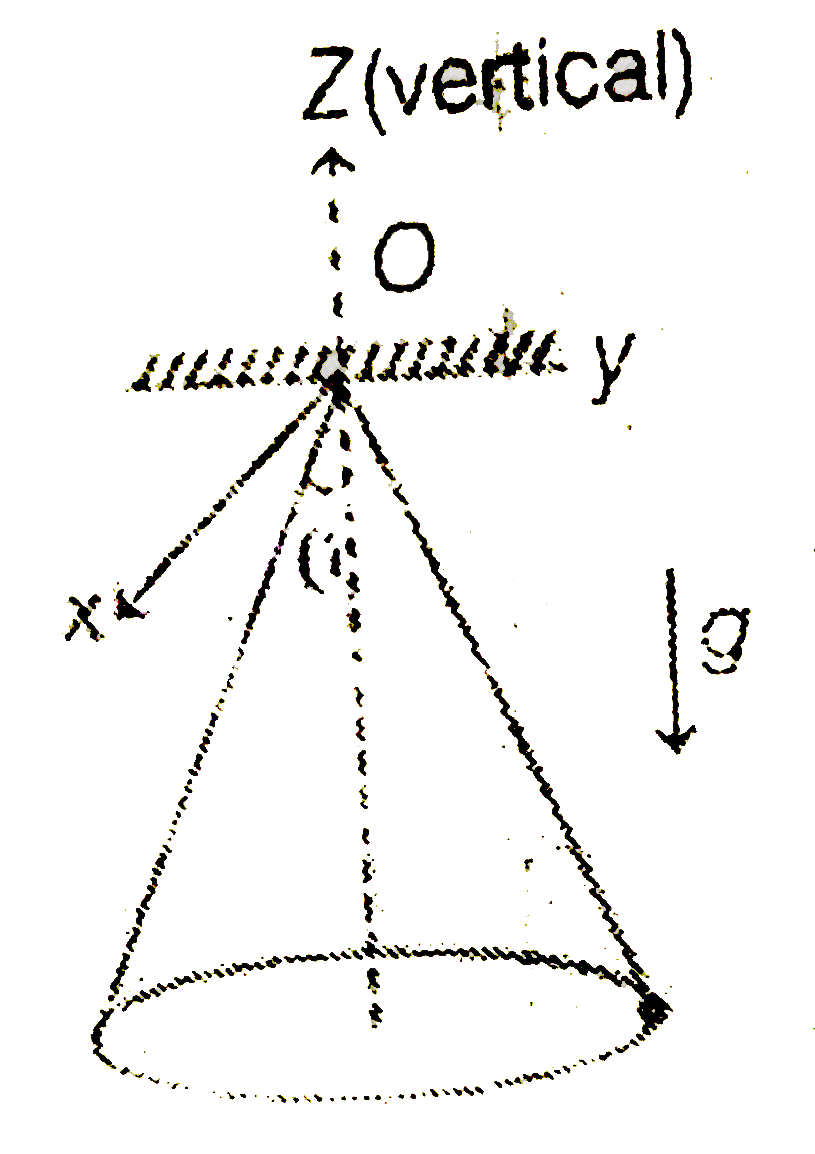
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.
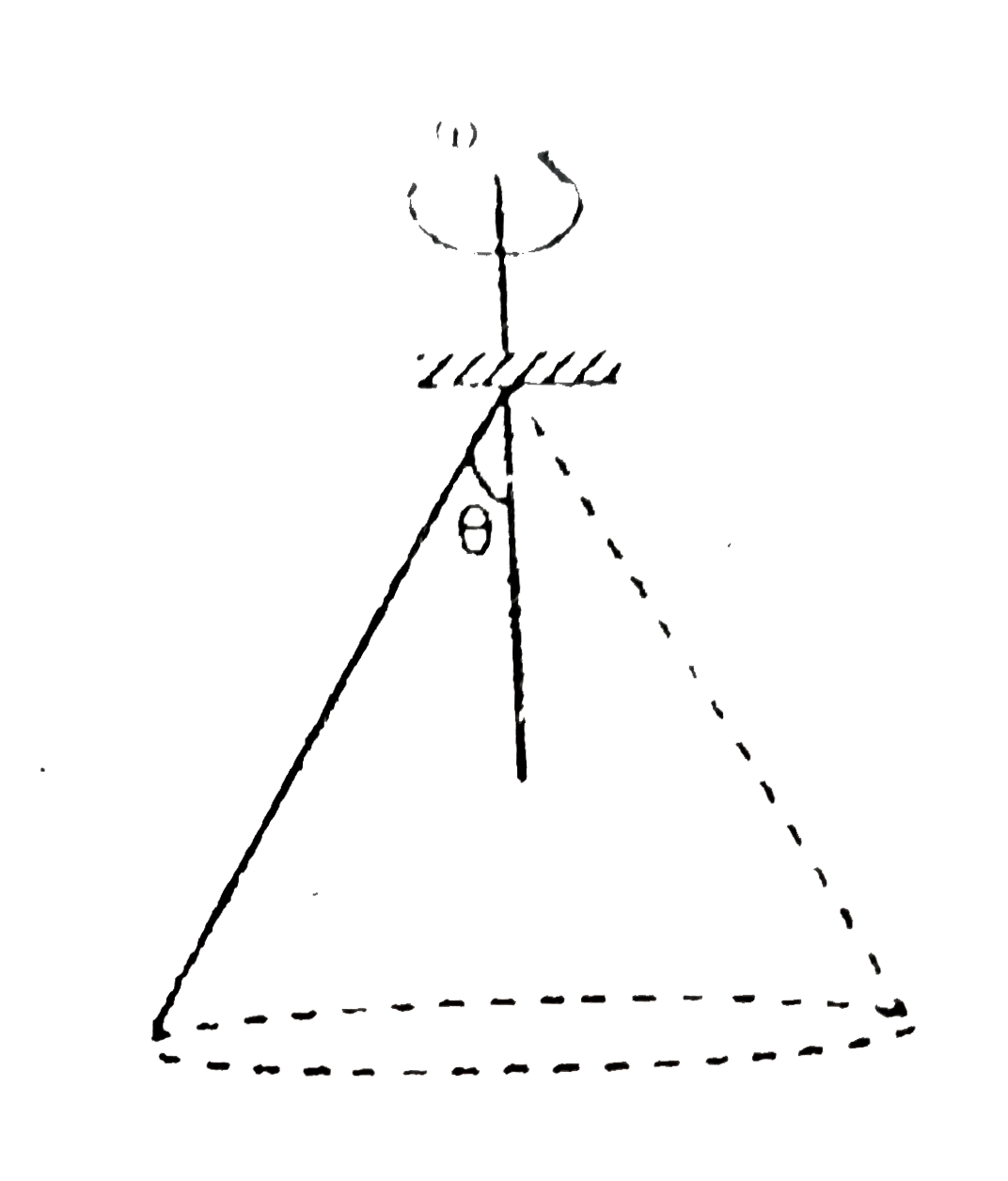
View SolutionA particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.
View SolutionA 1N pendulum bob is held at an angle θ from the vertical by a 2N horizontal force F as shown in figure. The The tension in the string supporting the pendulum bob (in newton) is
 .
.
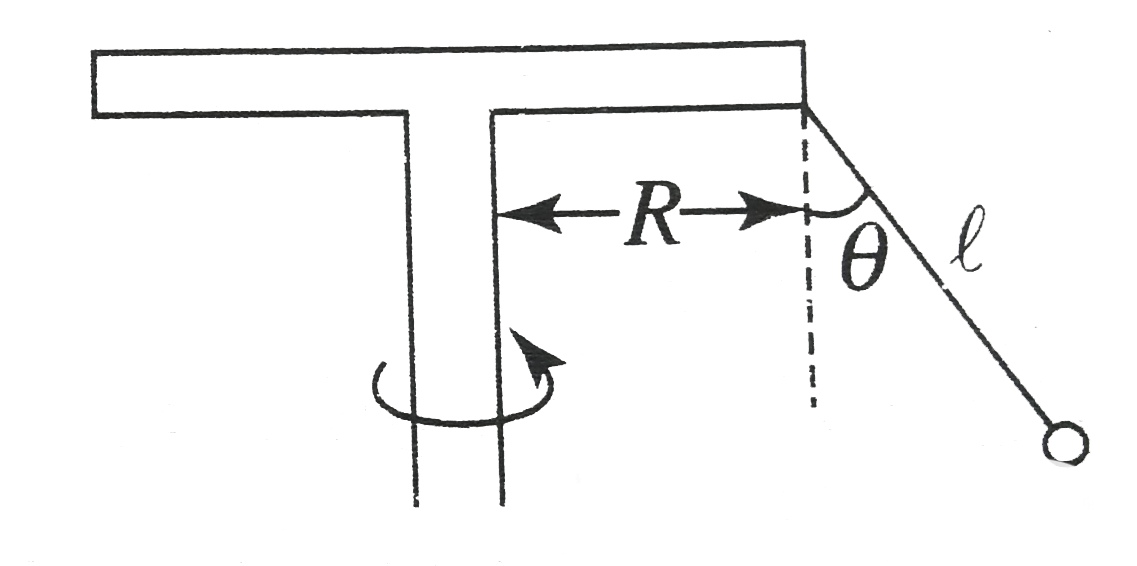
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
View Solution

