A playground merry-go-round of radius has a moment of inertia and is rotating about a frictionless, vertical axle. Facing axle, a child hops onto the merry-go-round and manages to sit down on the edge. The new angular speed of the merry-go-round is.
The correct Answer is:C
( c) From conservation of angular momentum,
=
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Work And Energy In Case Of Rotation
Explore 22 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Torque , Torque Equation And Equilibrium Of A Rigid Body
Explore 29 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A boy sitting on a merry-round make 200 revolutions per minute . Calculate the angular speed of the merry-go-round.
View SolutionA playground merry-go-round has radius 2m and moment of inertia 2000kgm2 about a vertical axle through its center.
(a) A boy applies 50N force tangentially to the edge of the merry-go-round for 20s. If the merry-go-round is initially at rest, what is its angular speed after 20s?
(b) How much work did the boy do on the merry-go-round?
(c) What is the average power supplied by the child?
(d) What is the instantaneous power supplied by the child at t=20s?
View Solution
Knowledge Check
A playground merry-go-round is at rest, pivoted about a frictionless axis. A child of mass m runs along a path tangential to the rim with speed v and jumps on to the merry-go-round. If R is the radius of the merry-go-round and I is its moment of inertia, then the angular velocity of the merry-go-round is
AmvRmR2+IBmvRICmR2mvRDImvR
A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round isA√Iω2−mv2IB√(I+mR2)ω2−mv2ICIω−mvRID(I+mR2)ω−mvRIIn a playground there is a merry-go-round of mass 120 kg and radius 4 m. The radius of gyration is 3m. A child of mass 30 kg runs at a speed of 5 m/sec tangent to the rim of the merry-go-round when it is at rest and then jumps on it. Neglect friction and find the angular velocity of the merry-go-round and child
A0.2 rad/secB0.1 rad/secC0.4 rad/secD0.8 rad/sec
A wheel of moment of inertia 0.500kg−m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
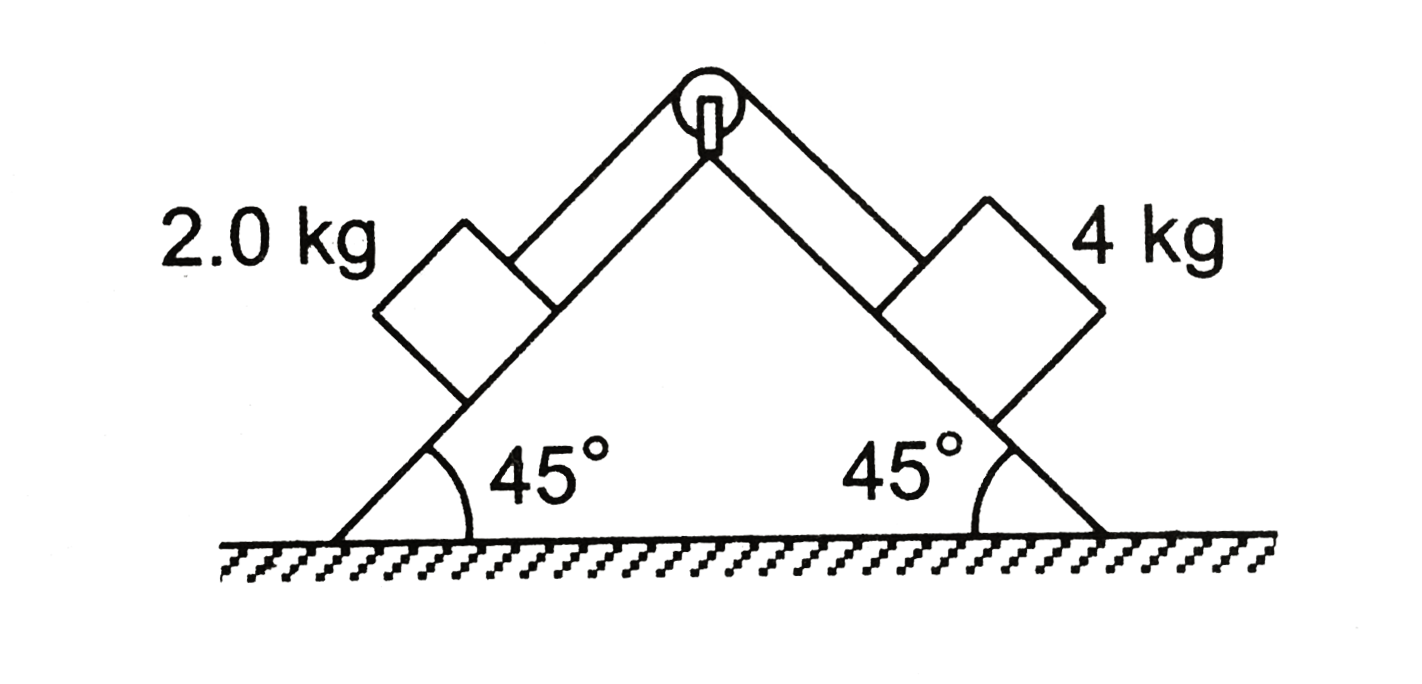
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
View SolutionTwo identical twins, Tui and Kui are playing on a large merry go round in an amusement park. The surface of merry go round is frictionless and is turning at a constant rate of revolution as the twins ride on it. Tui, sitting 2 m from the center of the merry go round, must hold onto one of the metal posts attached to the merry go round with a horizontal force of 90N to keep from sliding off. Kui is sitting at the edge, 4m from the center. With what horizontal force must she hold on to keep form falling off ?
View SolutionA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)

View SolutionA girl of mass M stands on the rim of a frictionless merry-go-round of radius R and rotational inertia I that is not moving. She throws a rock of mass m horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is v. After, the linear speed of the girl is.
 .
.
View Solution

