A rigid mass less rod of length L is hinged at its one end a weight W is hung at a distance l(<L) from this end.
What is force P should be applied upwards at the other end so that the rod remains in equilibrium horizontally ?
 .
.
W(L−l)L
W(L−l)l
WlL
WLl
The correct Answer is:C
( c) Taking torque about hinge A.
PL−Wl=0⇒P=WlL.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation
30 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Work And Energy In Case Of Rotation
22 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotational Kinematics
19 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
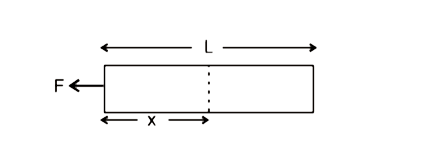
A horizontal force is applied on a uniform rod of length L kept on a frictionless surface. Find the tension in rod at a distance 'x' from the end where force is applied
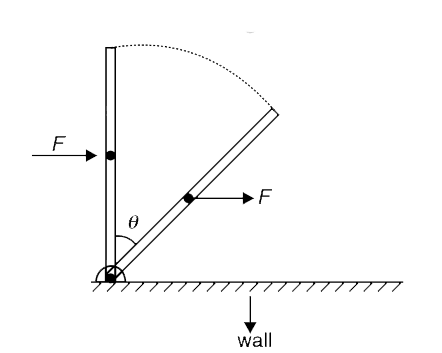
View SolutionA uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle θ (see figure) the hinge force will make a 45∘ angle with the rod ?
View Solution
Knowledge Check
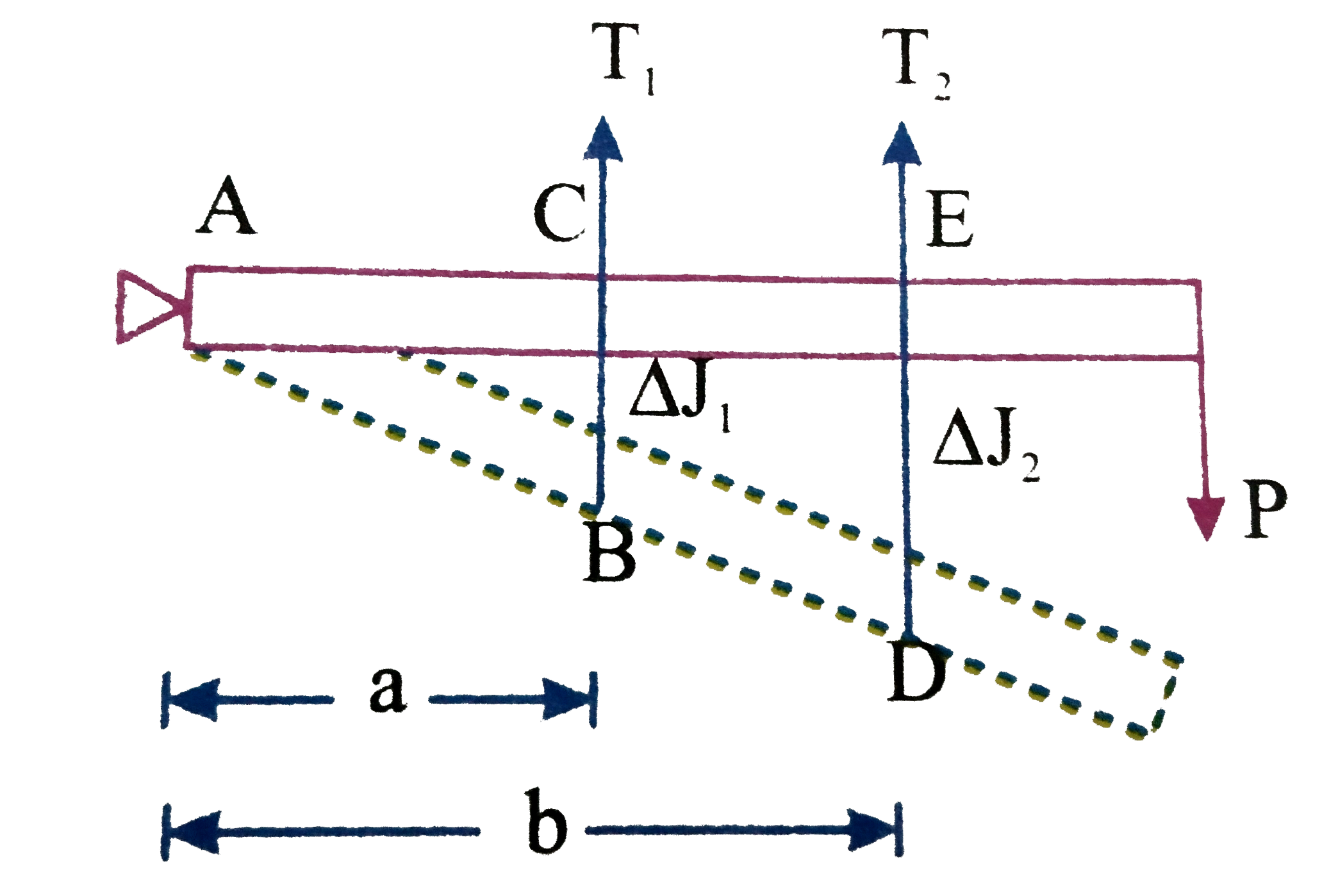
A massless rod of length l is hinged at one end and is held horizontal by two identical vertical wires, which are tied at distances a and b form the hinged end. A load P si applied at the free end of the rod.
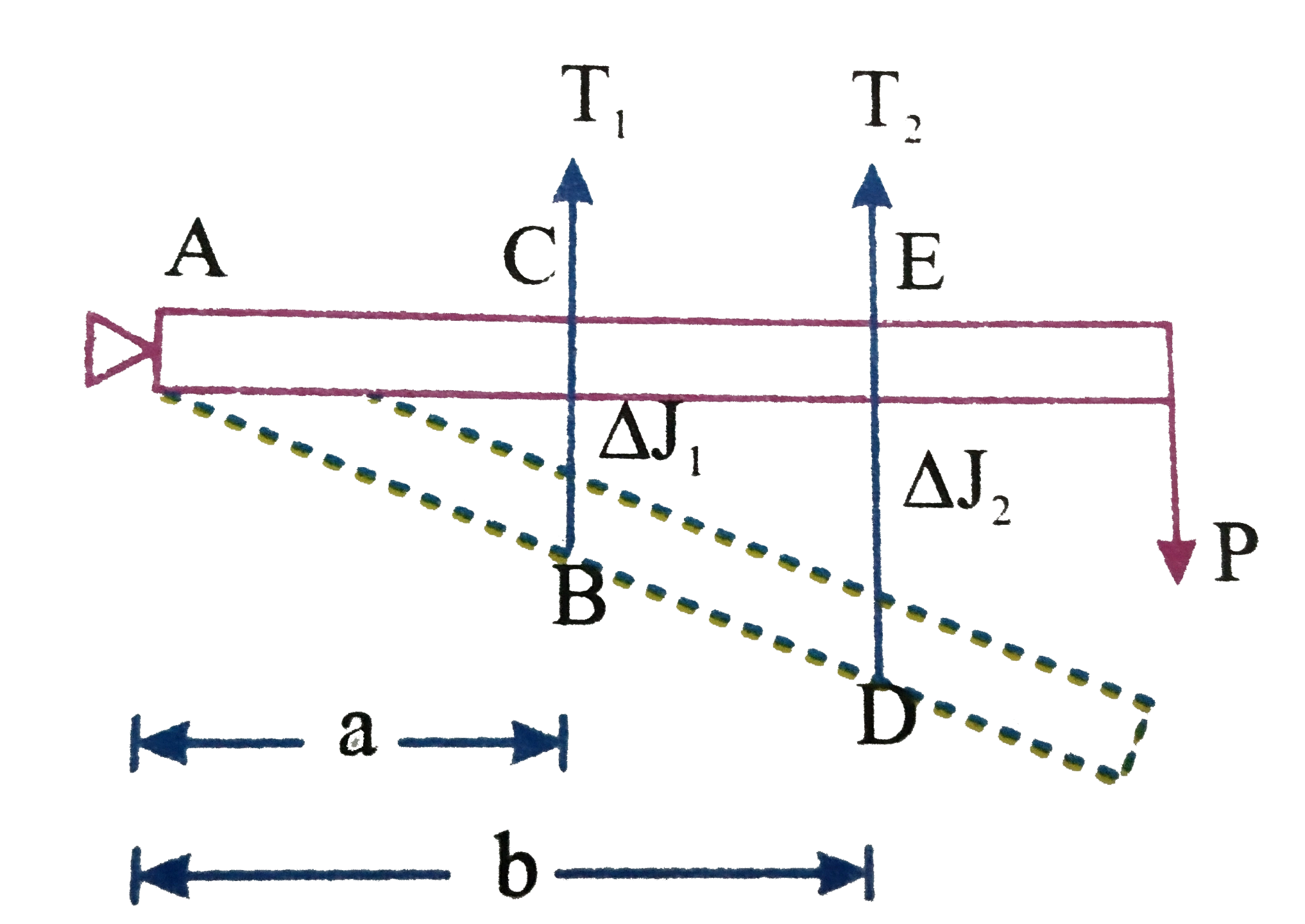
The tension in the first isAPla2+b2aBPla2+b2bCPla+baDPla+bbA massless rod of length l is hinged at one end and is held horizontal by two identical vertical wires, which are tied at distances a and b form the hinged end. A load P si applied at the free end of the rod.
The tension in the secound wire isAPla2+b2aBPla2+b2bCPla+baDPla+bbA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mg
In the figure a uniform rod of mass 'm' and length 'l' is hinged at one end and the other end is connected to a light vertical of spring constant 'k' as shown in figure. The spring has extension such that rod is equilibrium when it is horizontal . The rod rotate about horizontal axis passing through end 'B'. Neglecting friction at the hinge find (a) extension in the spring (b) the force on the rod due to hinge.
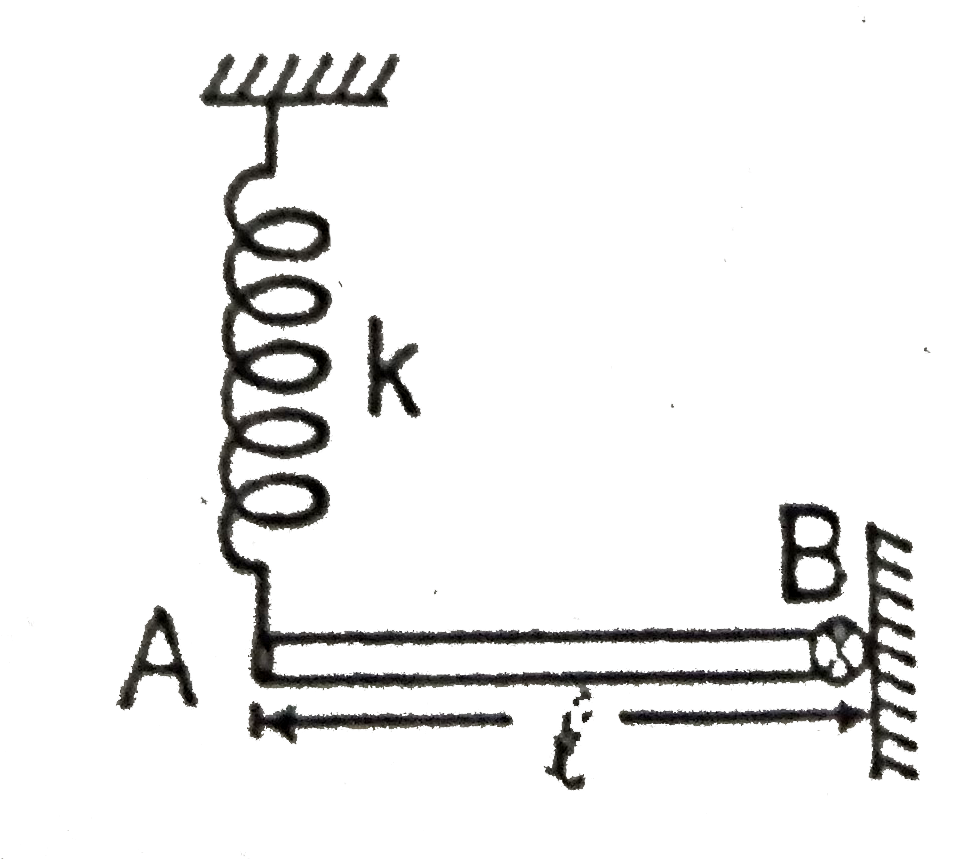
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
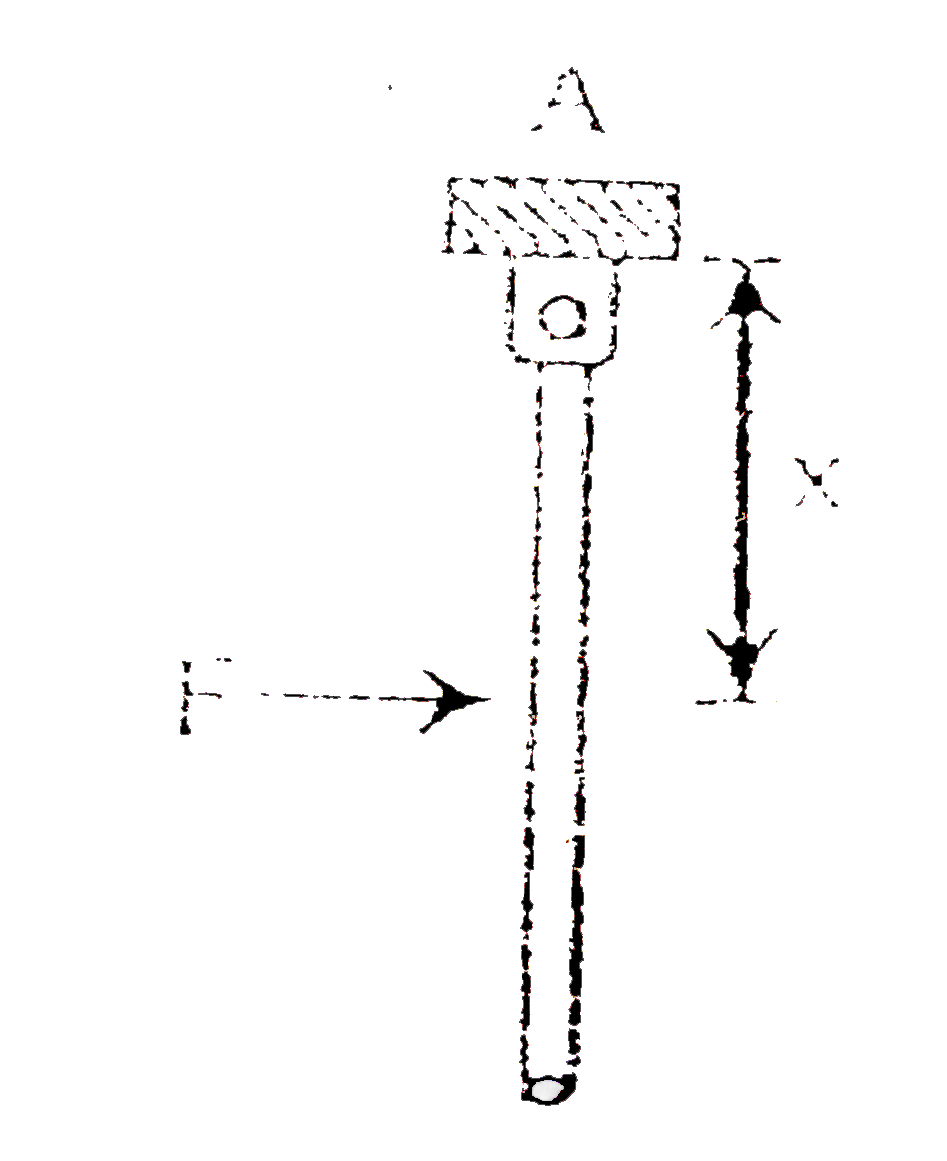
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass (a) variea with x as:
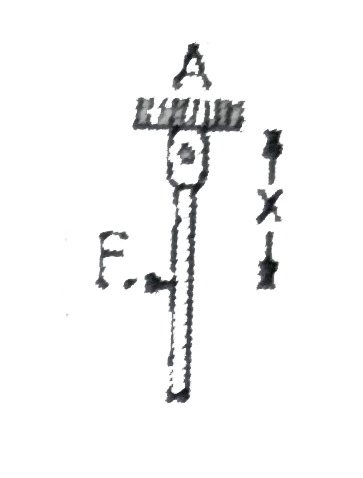
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View Solution
