A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
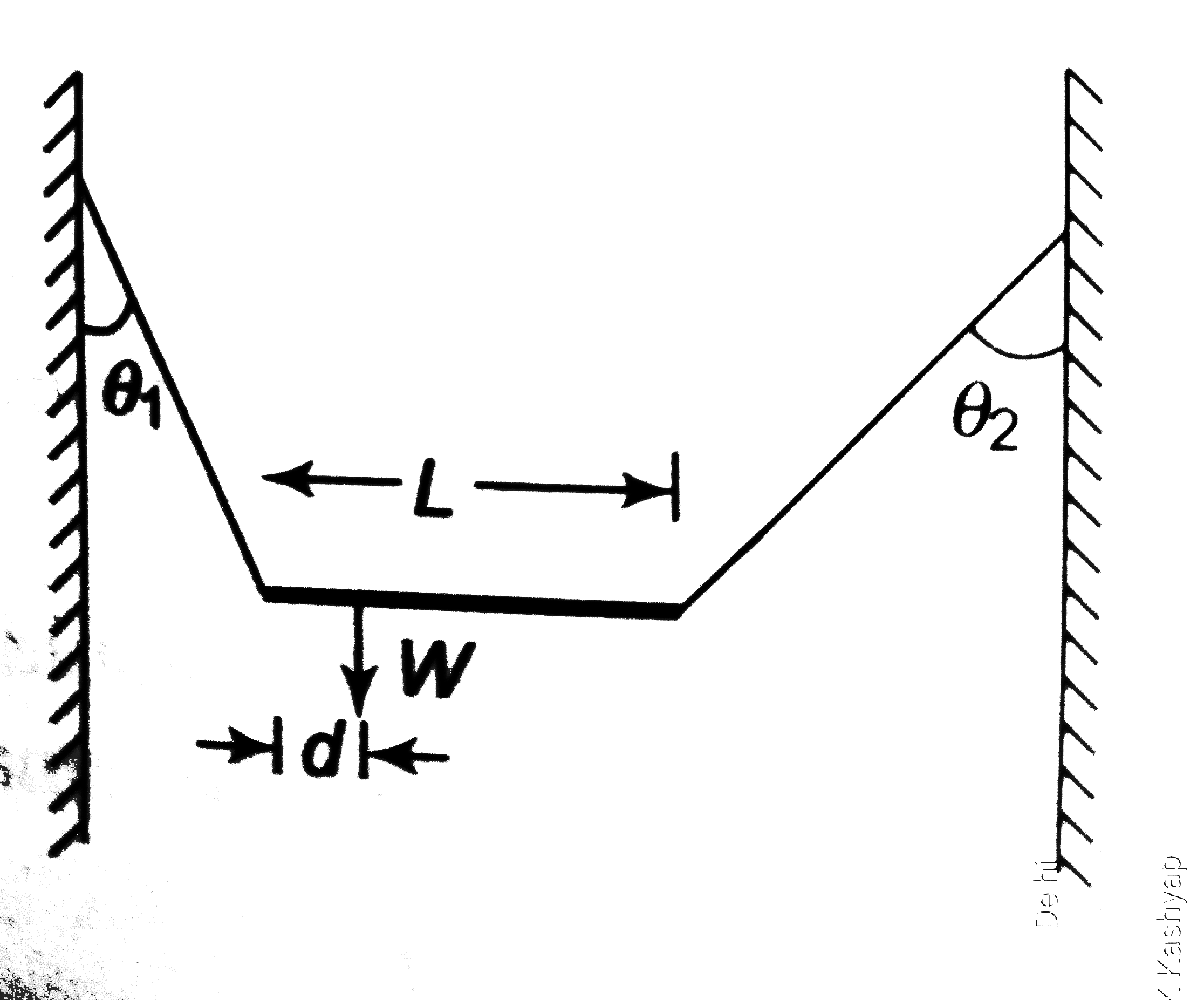 .
.
L(tanθ1+tanθ2tanθ1)
L(tanθ1tanθ1+tanθ2)
L(tanθ2tanθ1+tanθ2)
L(tanθ1+tanθ2tanθ2)
The correct Answer is:B
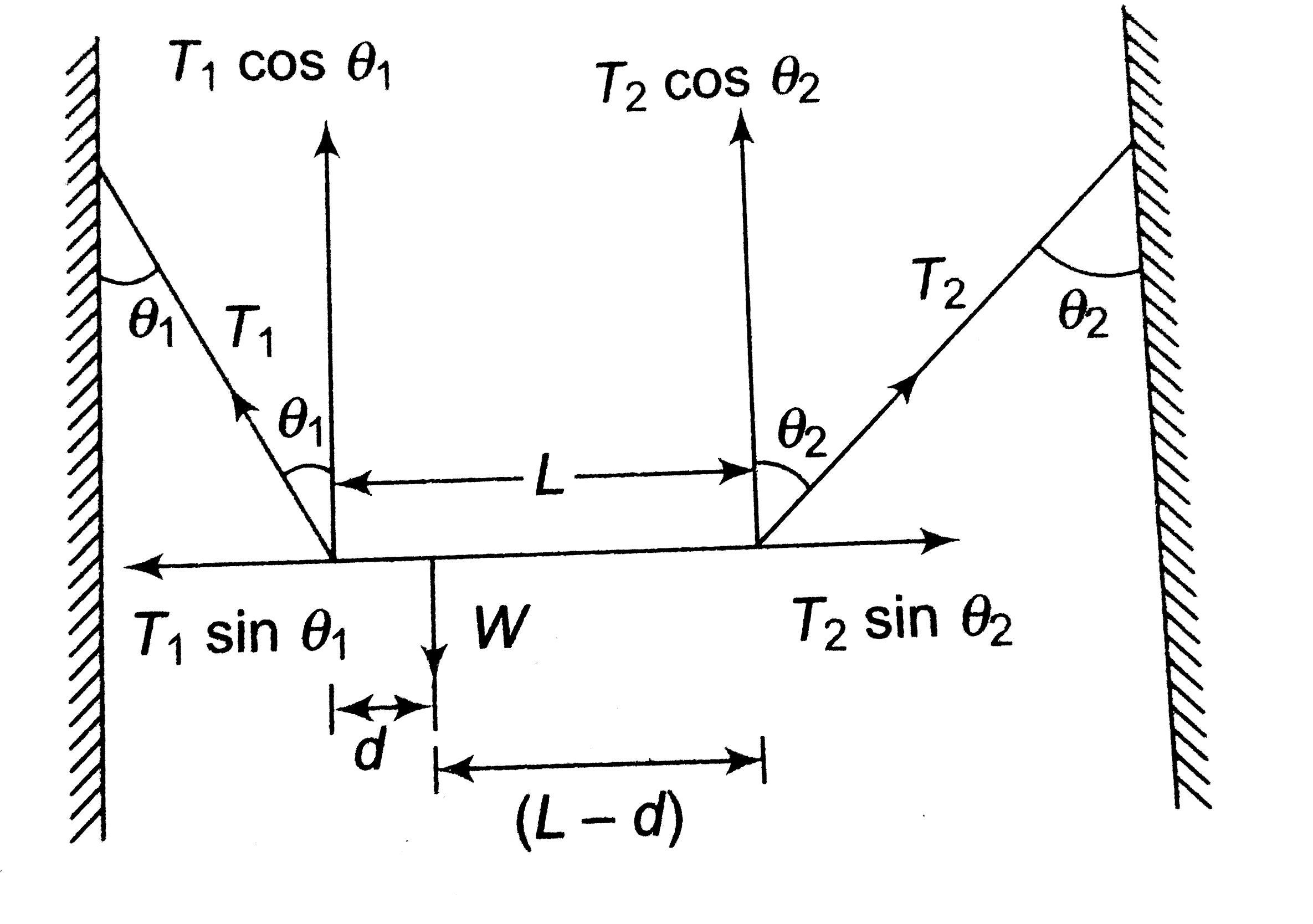
(b) Let T1 and T2 be the tensions in two strings as shown in the figure.
For translational equilibrium along the horizontal direction, we get
T1sinθ1=T2sinθ2 …(i)
For ratational equilibrium about G
−T1cosθ1d+T2cosθ2(L−d)=0
T1cosθ1d=T2cosθ2(L−d) ...(ii)
Dividing equation (i) by (ii), we get
tanθ1d=tanθ2(L−d) or L−dd=tanθ2tanθ1
(Ld−1)=tanθ2tanθ1⇒Ld=(tanθ2tanθ1+1)
Ld=tanθ2+tanθ1tanθ1
d=L(tanθ1tanθ1+tanθ2).
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Angular Momentum And Its Conservation
Explore 30 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Work And Energy In Case Of Rotation
Explore 22 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotational Kinematics
Explore 19 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9∘and53.1∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
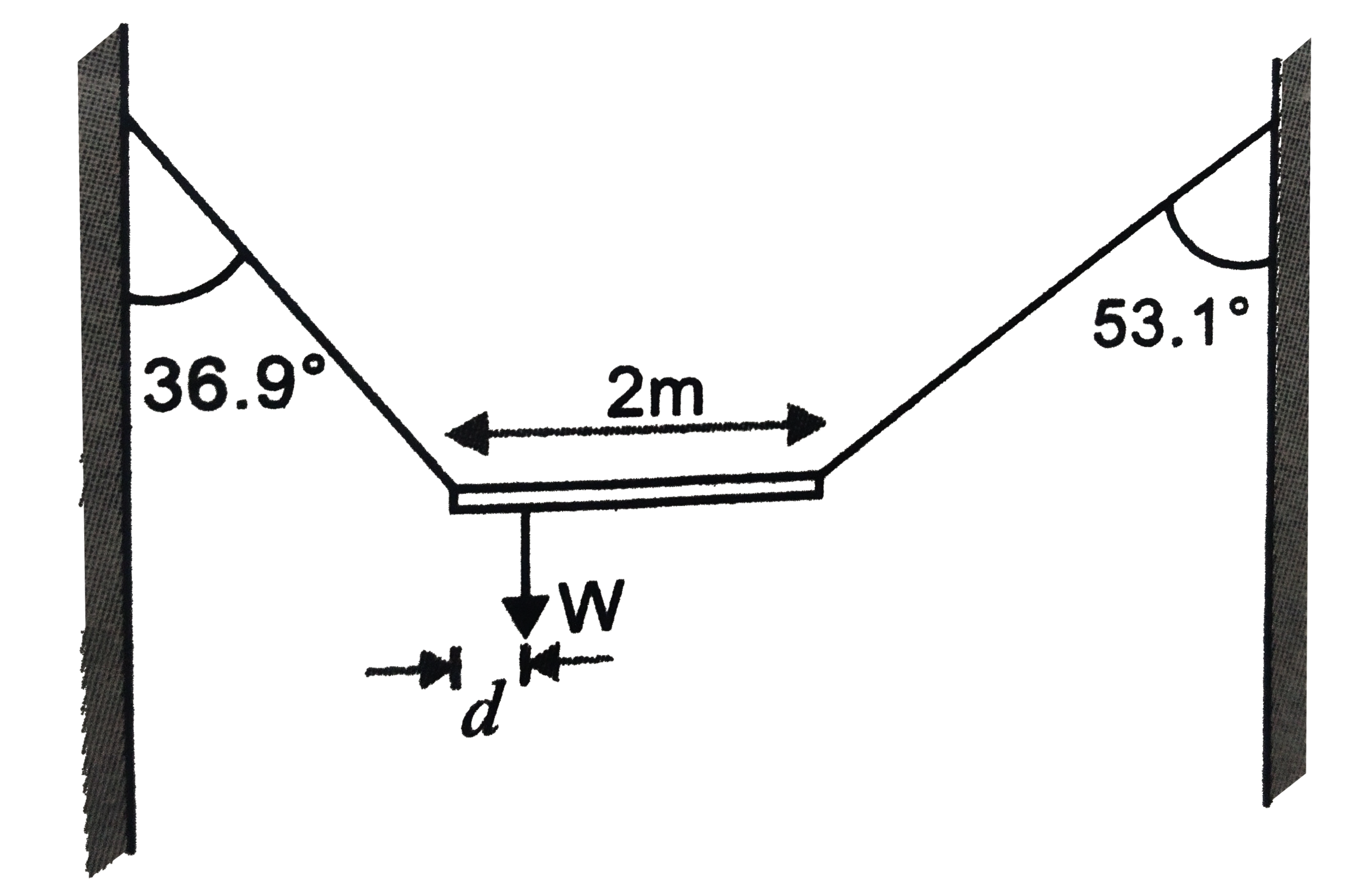
View SolutionA non-uniform bar of weight W is suspended at rest by two string of negligible weights as shown in figure. The angle made by the string with the vertical are 36.9∘ and 53.1∘ respectively. The bar 2m long. Calculate the distance of the centre of gravity (in cm ) of the bar from it left end.
'(##CEN_KSR_PHY_JEE_C09_E01_033_Q19##)'
View Solution
Knowledge Check
A non-uniform bar of weight w is suspended at rest by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are 37∘ and 53∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end. given sin37∘=3/5 and sin53∘=4/5
 A72cmB64cmC100cmD40cm
A72cmB64cmC100cmD40cmA uniform rod of length l and mass m is suspended by two vertical inextensible strings as shwon in figure. Then, tension in the left string when right string snape, si
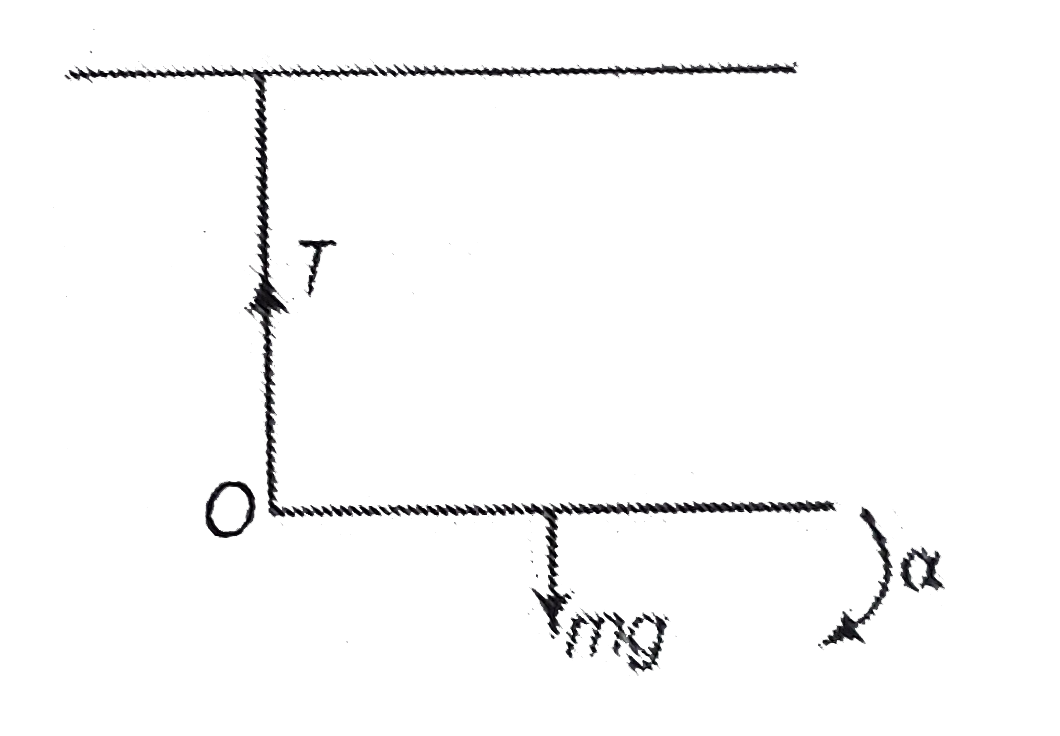 A3mg4Bmg4Cmg2Dmg8
A3mg4Bmg4Cmg2Dmg8A uniform sphere of weight W and radius 3 m is being held by a frictionless wall as shown in the figure. The tension in the string will be:
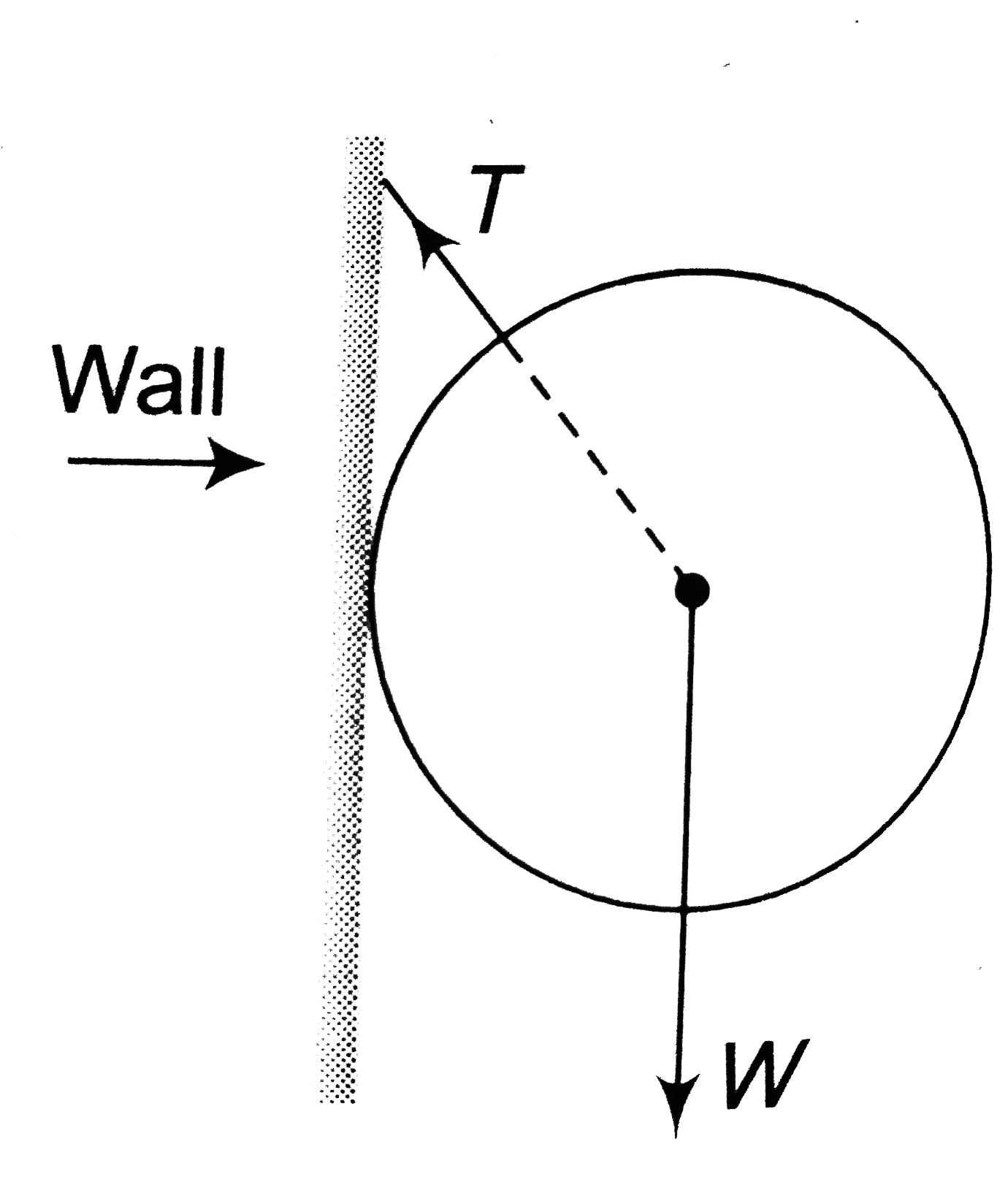 A5W/4B15W/4C15W/16Dnone of these
A5W/4B15W/4C15W/16Dnone of these
A uniform sphere of weight W and radius 5 cm is being held by string as shown in the figure. The tension in the string will be
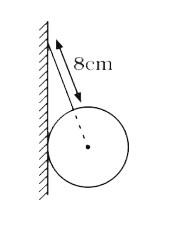
View SolutionA uniform rod of length l and mass M is suspended on two vertical inextensible string as shown in figure. Then tension T in the left string at the instant, when right string snaps is?

View SolutionA uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is

View Solution

