Two identical balls A and B are released from the position shown in Fig. They collide elastically with each other on the horizontal portion. The ratio of heights attained by A and B after collision is (neglect friction)

1:4
2:1
4:13
2:5
After collision the balls exchange theirt velocity their velocities, i.e.,
vA=√2ghandvB=√2g(4h)=2√2gh

Height attained by A will be : hA=v2A2g=h
But path of B will be first straight line and then parabolic as shown in figure. After calculation we can shown that : hB=134handhAhB=413
Topper's Solved these Questions
Similar Questions
A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30∘ with the original line of motion. Find the speeds of the two balls after collision.
View SolutionA ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

If track makes an angle 30∘ with horizontal at B, then maximum height attained by ball will be
View Solution
Knowledge Check
A small ball of mass m collides elastically with a simple pendulum with bob of mass ma at rest. The macimum height attained by the bob after collision is
Av2gBv22gCv24gD0Two stones A and B are thrown at an angle of 50∘ from the horizontal. The velocity of B is twice of the velocity of A. The ratio in the greatest heights attained by A and B is
A1/2B1/4C1/8DNone of theseTwo stones A and B are thrown at an angle of 50∘ from the horizontal. The velocity of B is twice of the velocity of A. The ratio in the greatest heights attained by A and B is
A1/2B1/4C1/8DNone of these
In the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
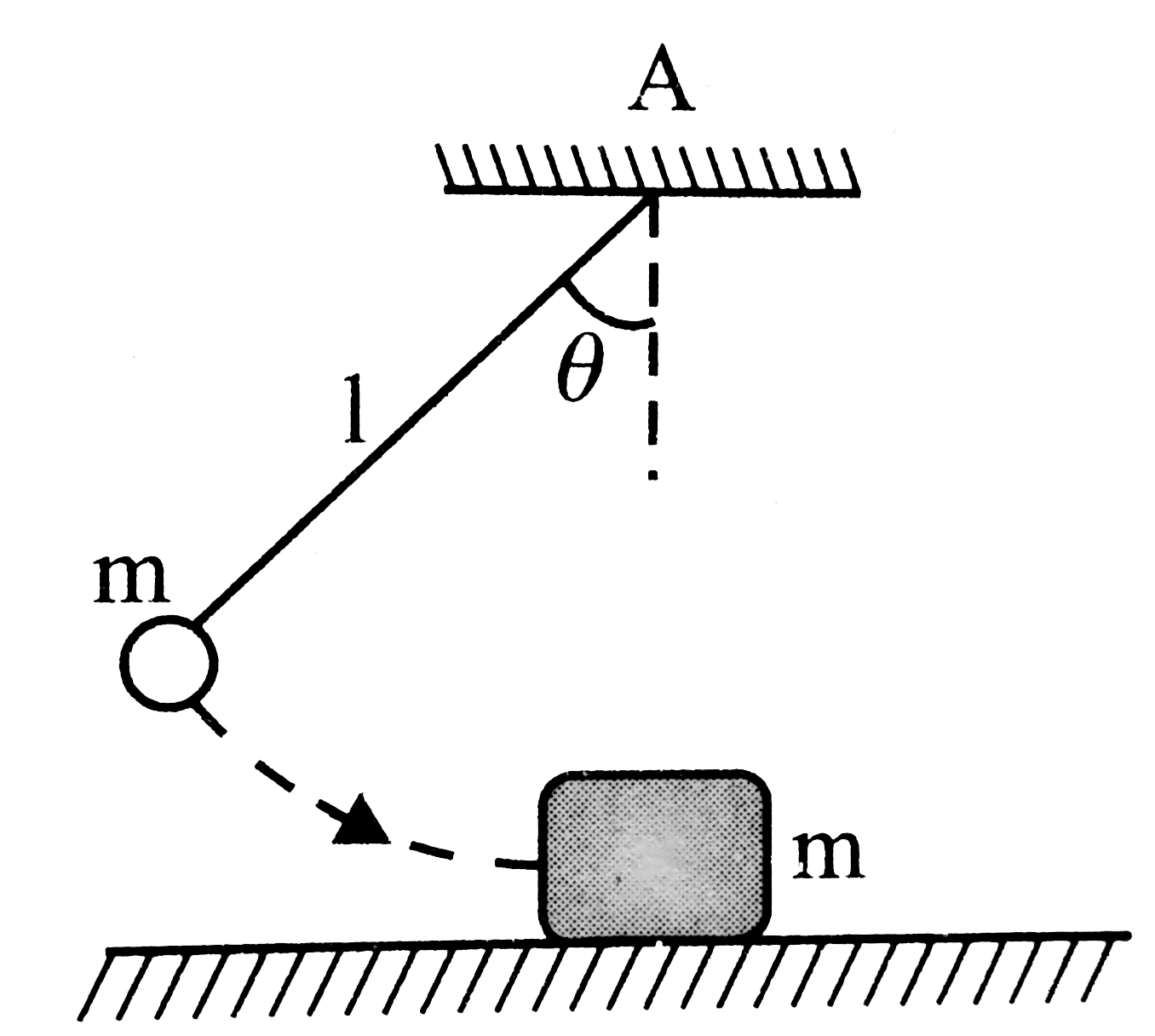
The velocity of block just after collision is
View SolutionIn the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
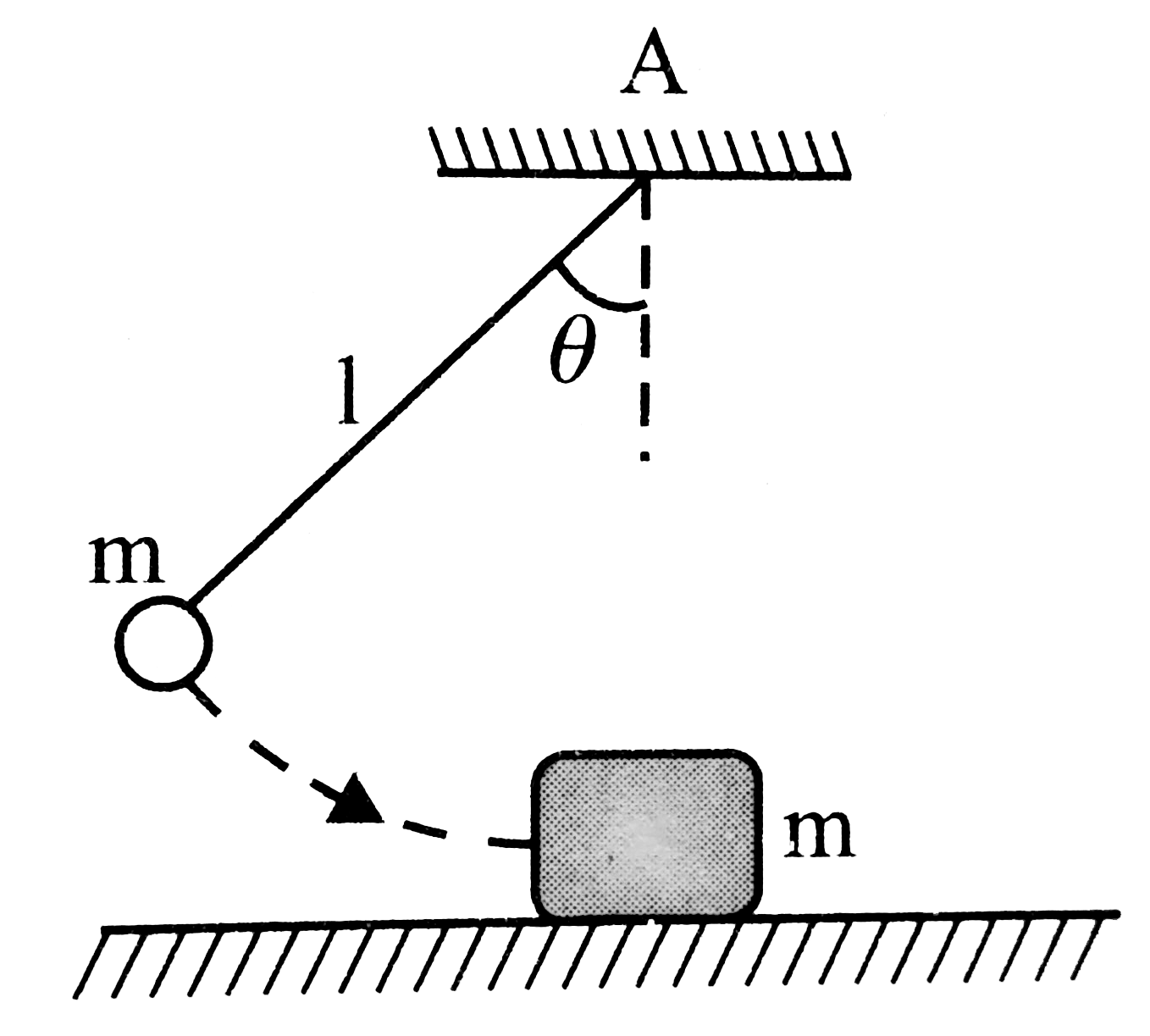
The coefficient of restitution for collision between the ball and the block is
View SolutionTwo balls A and B of angular velocities ωA and ωB collide with each other. Then, after collision
View SolutionTwo identical balls each moving with speed v at right angle to each other collide perfectly inelastically. Their speed after collision is
View SolutionTwo identical bodies moving in opposite direction with same speed, collide with each other. If the collision is prefectly elastic then
View Solution
