The velocity vector of a sphere after it hits a vertical wall which is pallel to ˆj is (−ˆi+3ˆj) on a smooth horizontal surface. The coefficient of restitution between ball and wall is (1/2). Final the velocity vector of sphere immediately before collision.
ˆi+3ˆj
−2ˆi+3ˆj
−ˆi+3ˆj
2ˆi+3ˆj
The correct Answer is:B
Component of velocity parellel to wall will remain unchanged. (3ˆj) willl remain same . (ˆi) component
will become (−ˆi)×(−1e)=(−ˆi)(−2)
Velocity vector of sphere immediately before collision
=2ˆi+3ˆj
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A smooth sphere of mass m is moving on a horizontal plane with a velocity 3ˆi+ˆj when it collides with a vertical wall which is parallel to the ˆj vector. If the coefficient of restitution between the sphere and the wall is 1/2. find
a. the velocity of the sphere after impact,
b. the loss in kinetic energy caused by the impact.
c. the impulse that acts on the sphere.
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj and the coefficient of restitution of the sphere and the wall is e=12. Find the velocity of the sphere after it hits the wall?
View Solution
Knowledge Check
A smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj vector and the coefficient of restitution between the sphere and the wall is e=1/2. The velocity vector of the sphere after it hits the wall is
Aˆi−ˆjB−ˆi+2ˆjC−ˆi−ˆjD2ˆi−ˆjA smooth sphere is moving on a horizontal surface with velocity vector 3ˆi+ˆj immediately before it hits a vertical wall. The wall is parallel to the vector ˆj and the coefficient of restitution between the wall and sphere is 13. The velocity vector of the sphere after it hits the wall is :-
Aˆi+ˆjB3ˆi−13ˆjC−ˆi+ˆjDˆi−ˆjA smooth sphere is moving on a horizontal surface with velocity vector 3ˆi+ˆj immediately before it hits a vertical wall. The wall is parallel to the vector ˆj and the coefficient of restitution between the wall and the sphere is 1/3. The velocity vector of the sphere after it hits the wall is :
A3ˆi−13ˆjB−ˆi+ˆJCˆi−ˆjD−ˆi−13ˆj
A ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionThe two diagrams show the situation before and after a collision between two spheres A and B of equal radii moving along the same straight line on a smooth horizontal surface. The coefficient of restitution e is
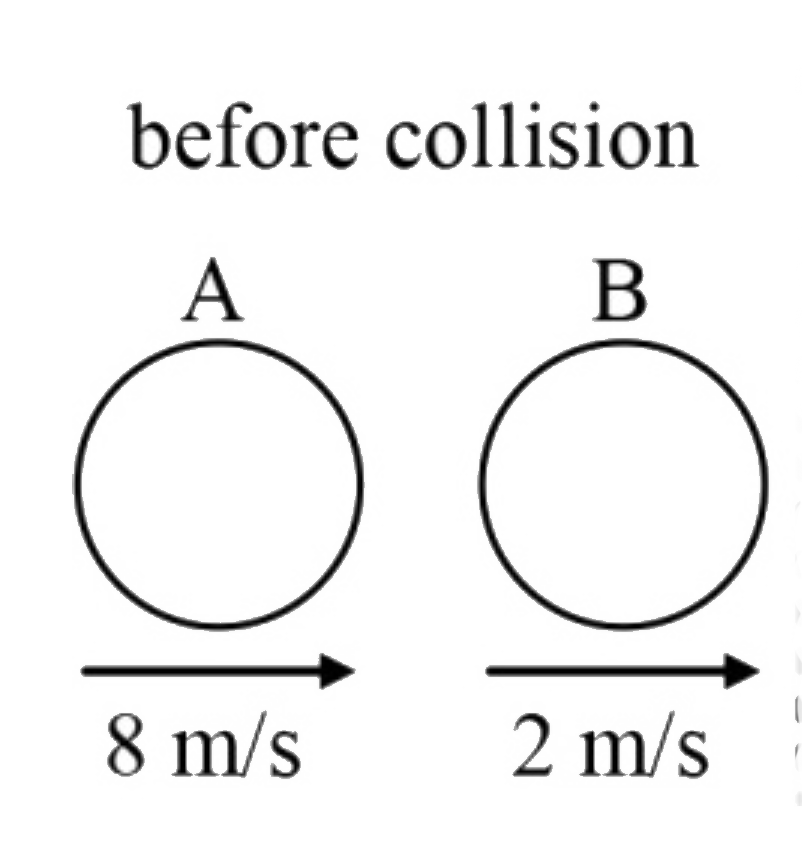
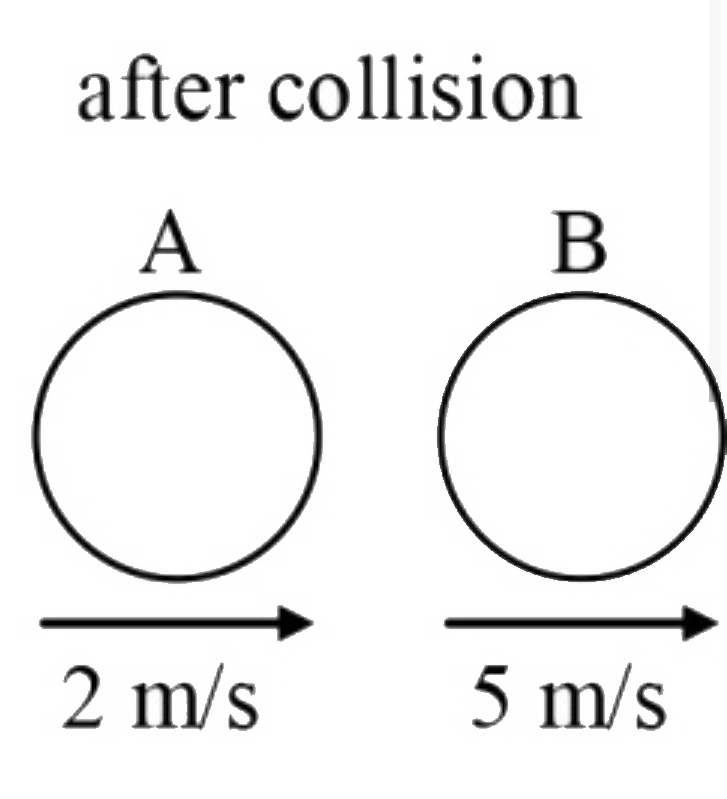
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View SolutionA ball falls from a height of 10m on to a horizontal plane. If the coefficient of restitution is 0.4, then the velocity with which it rebounds from the plane after second collision is
View Solution

