The bob A of a simple pendulum is released when the string makes an angle of 45∘ with the vertical. It hits another bob B of the same meterial and same mass kept at rest on the table. If the collision is elastic, then

Both AandB rise to the same height
Both AandB comes to rest at B
Both AandB move with the same velocity of A
A comes to rest and B move with the same velocity of A
The correct Answer is:D
Due to the same mass of A and B as well as due to elastic collision velocities of spheres get interchanged after the collision.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
The bob A of a simple pendulum released from 30∘ to the vertical hits another bobo B of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.
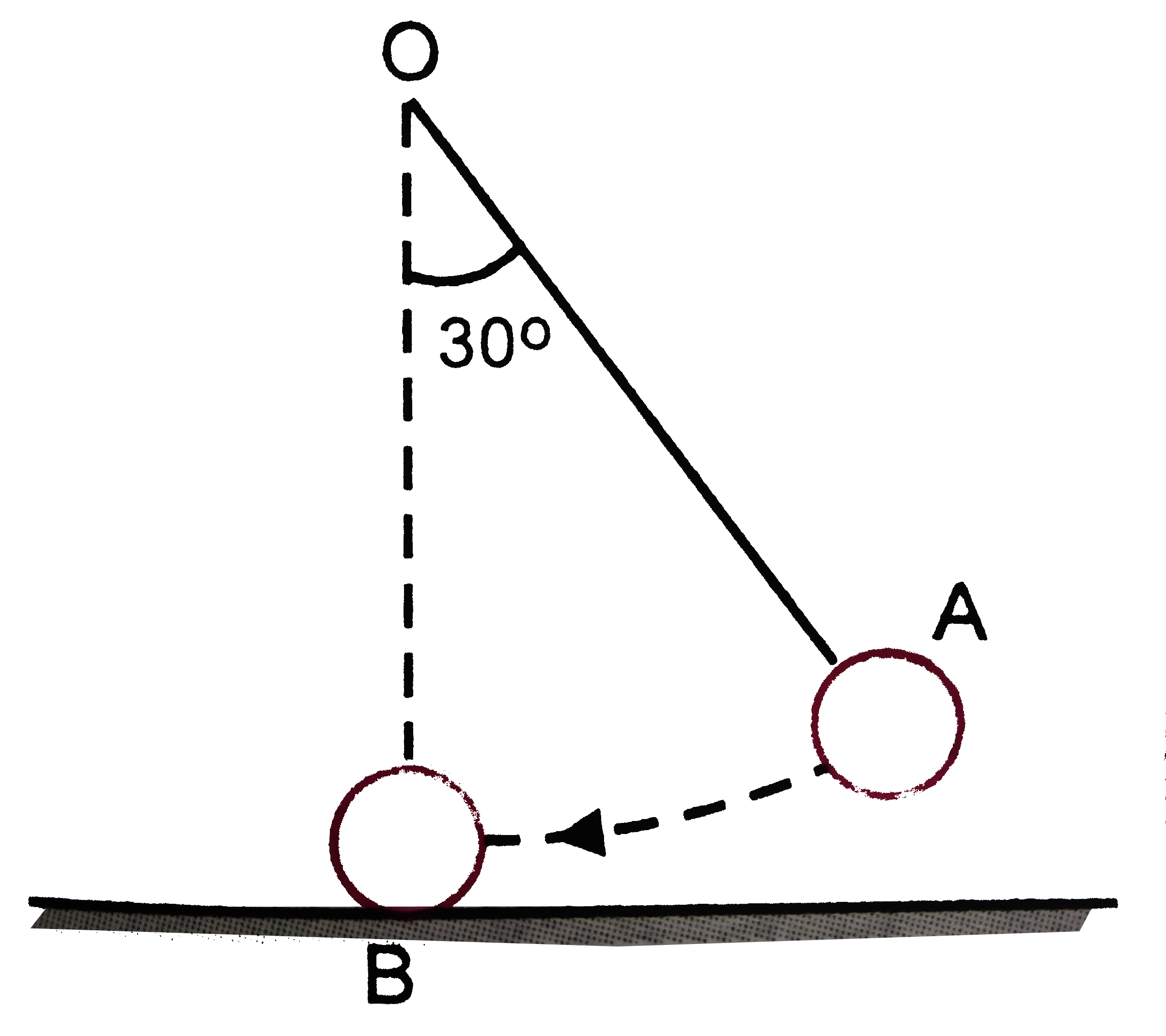
View SolutionThe bob of a pendulum of length 980 cm is released from rest with its string making an angle 60∘ with the vertical. It collides with a ball of mass 20 gm resting on a smooth horizontal surface just at the position of rest of the pendulum. With what velocity will the bob move immediately after the collision? What will be the maximum angular displacement of the bob after them collision ? The mass of the bob is 10 gm. '
View Solution
Knowledge Check
when the bob of a simple pendulum swings, the work done by bob in the string is :
A>0B<0CzeroDmaximumIf the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
AincreaseBremain sameCdecreasesDafirst increase and then decreasesA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
Aπ4Bcos−1(1√3)Csin−1(1√3)Dπ3
A nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60∘ with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
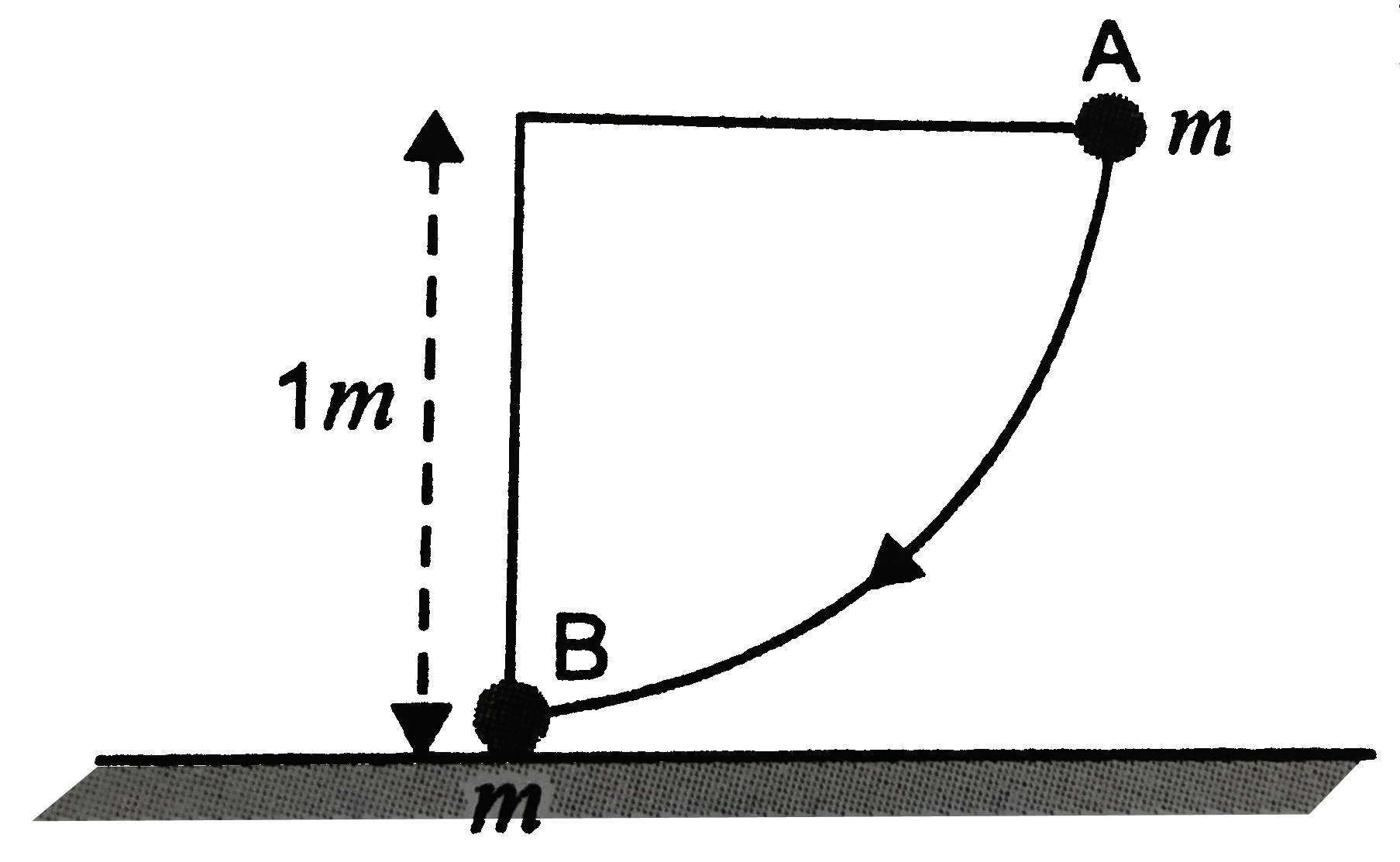
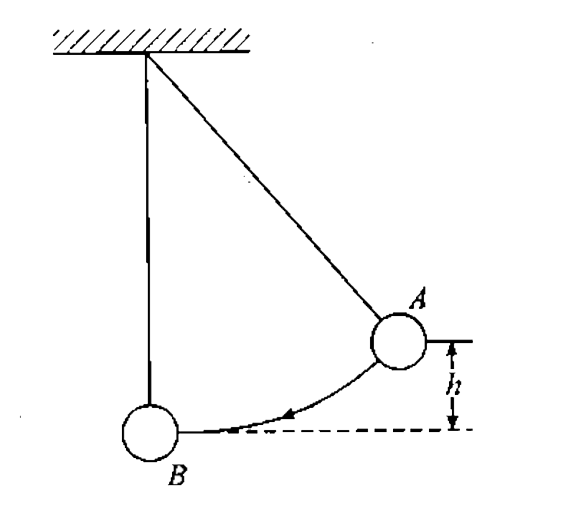
View SolutionThe bob A of a pendulum released from a height h hits head-on another bob B of the same mass of an identical pendulum initially at rest. What is the result of this collision? Assume the collisio to be elastic (see figure).
View SolutionA simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–

View SolutionA nail is fixed at a point P vertically below the point of suspension 'O' of simple pendulum of length 1m. The bob is released when the string of pendulum makes an angle 30∘ with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with P . The least distance of P from O is
View Solution

