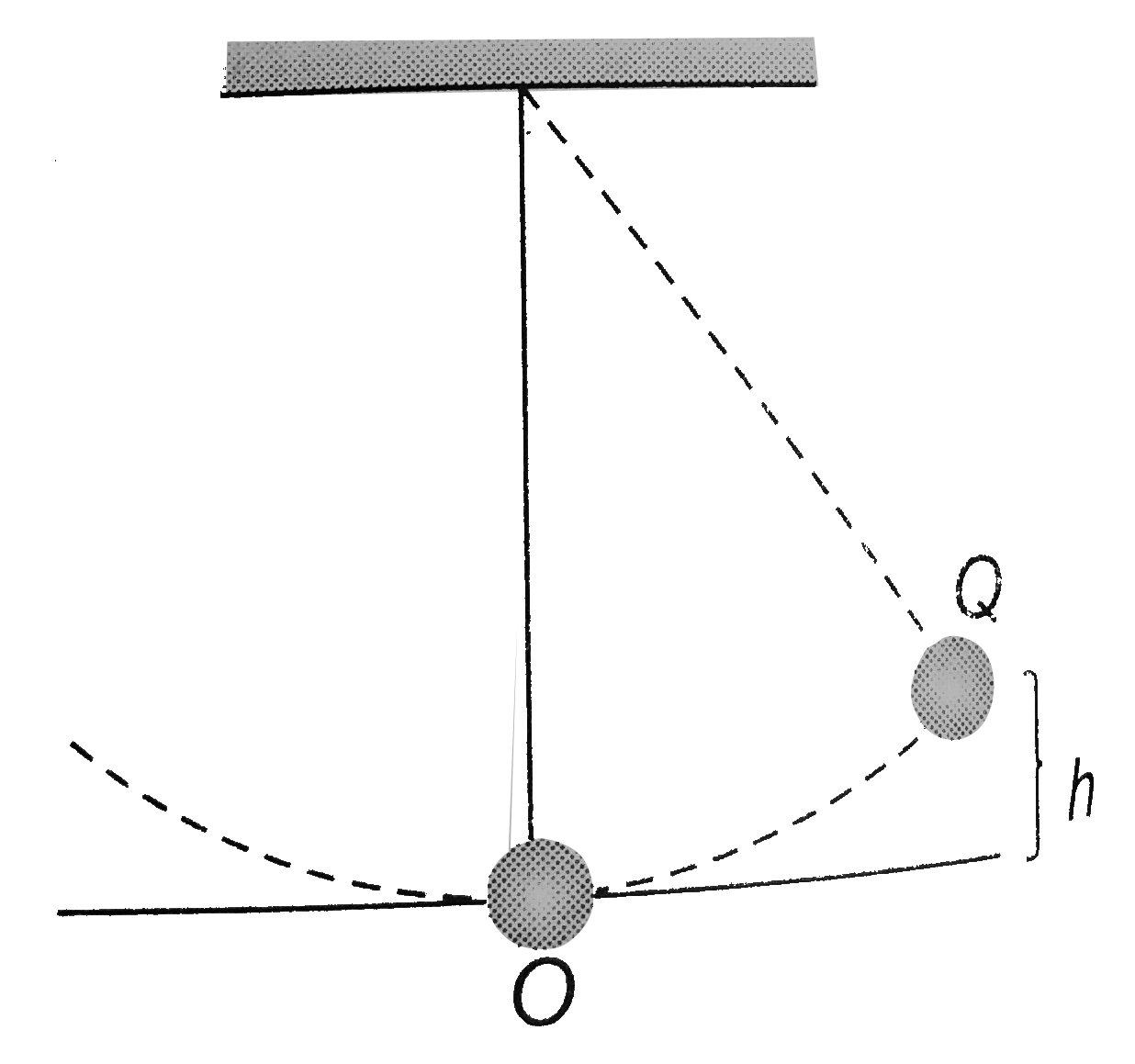
The bob of a simple pendulum it displaced position $O$ to a equilibrium position $Q$ which is at height h above $O$ and the bob to then mass released Assuming the mass of the bob is m and time period $2.0$ sec of oscillation to be string when the bob passes through $O$ is

$m (g + π \sqrt{2 g h})$

$m (g + \sqrt{π^{2} g h})$

$m (g + \sqrt{\frac{π^{2}}{2} g h})$

$m (g + \sqrt{\frac{π^{2}}{3} g h})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The bob of a simple pendulum it displaced position $O$ to a equilibrium position $Q$ which is at height it above $O$ and the bob to then mass released Assuming the mass of the bob to be m and $2.0$ sec of oscillation to be string when the bob passes through $O$ is

A $m (g + π \sqrt{2 g h})$
B $m (g + π \sqrt{π^{2} g h})$
C $m (g + \sqrt{\frac{π^{2}}{2} g h})$
D $m (g + \sqrt{\frac{π^{2}}{3} g h}$
The bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be $2.0 s$ , the tension in the string when the bob passes through 'O' is
A $m (g + 2 π^{2} h)$
B $m (g + π^{2} h)$
C $m (g + \frac{π^{2}}{2} h)$
D $m (g + \frac{π^{2}}{3} h)$
The bob of simple pendulum having length 1, is displaced from mean position to an angular position o with respect to vertical. If it is released, then velocity of bob at equilibrium position is
A $\sqrt{2 g (1 - cos θ)}$
B $\sqrt{2 g (1 + cos θ)}$
C $\sqrt{2 g l cos θ}$
D $\sqrt{2 g l}$