A car is negotisting a curved road of radius R . The road is banked at an angle theta. The coefficient of friction between the tyres of the car and the road is μs . The maximum safe velocity on this road is:
√gR2μs+tanθ1−μstanθ
√gRμs+tanθ1−μstanθ
√gRμs+tanθ1−μstanθ
√gR2μs+tanθ1−μstanθ
The correct Answer is:B
Vertical equilibrium
Ncoshtη=mg+fLsinθ
implies mg=Ncosθ−fLsinθ
(i) Horizontal equilibrium
(ii) Nsinθ+fLcosθ=mv2R
Eqn.(2)Eqn.(1)v2Rg=sinθ+μscosθcosθ+μssinθ
implies v=√Rg(sinθ+μscosθcosθ+μssinθ)
√Rg(tanθ+μs1−+μstanθ)
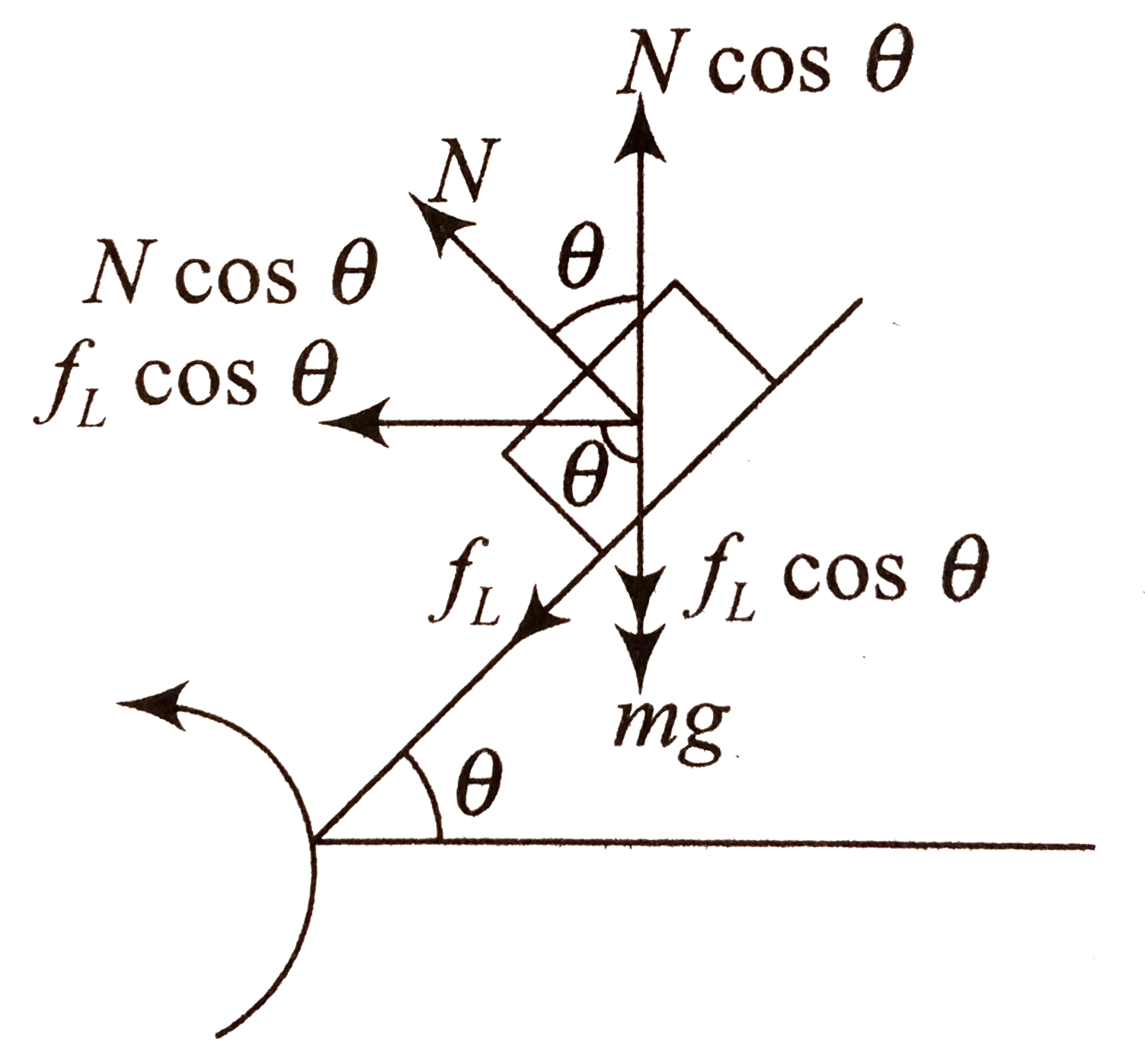
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:AIIMS Questions
Explore 26 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A car is moving on a horizontal circular road of radius 0.1 km with constant speed. If coefficient of friction between tyres of car and road is 0.4, then speed of car may be (g=10m/s2)
View SolutionA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is μ the car will skid if its speed exceeds .
View Solution
Knowledge Check
A car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficeint of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
A√gR(μs+tanθ1−μstanθ)B√gR(μs+tanθ1−μstanθ)C√g(R)2(μs+tanθ1−μstanθ)D√gR2(μs+tanθ1−μstanθ)A car is negotisting a curved road of radius R . The road is banked at an angle theta. The coefficient of friction between the tyres of the car and the road is μs . The maximum safe velocity on this road is:
A√gR2μs+tanθ1−μstanθB√gRμs+tanθ1−μstanθC√gμs+tanθR1−μstanθD√(gR2μs+tanθ1−μstanθ)A car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
AμRgB2μRgC(μRg)1/2D(2μRg)1/2
What is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ.
View SolutionWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ
View SolutionA circular road of radius 1000 m has banking angle 45∘. IF the coefficient of friction is between tyre and road is 0.5, then the maximum safe speed of a car having mass 2000 kg will be
View SolutionA car is travelling at 36 kmph on a road . The maximum turning radius of the car is 20 m ans g=10m/s2 .Then the coefficient of friction between its tyres and the road is
View SolutionWhat will be maximum speed of a car on a curved road of radius 30 m , If the coefficient of friction between the tyres and the road is 0.4?
(g=9.8m/s2)
View Solution

