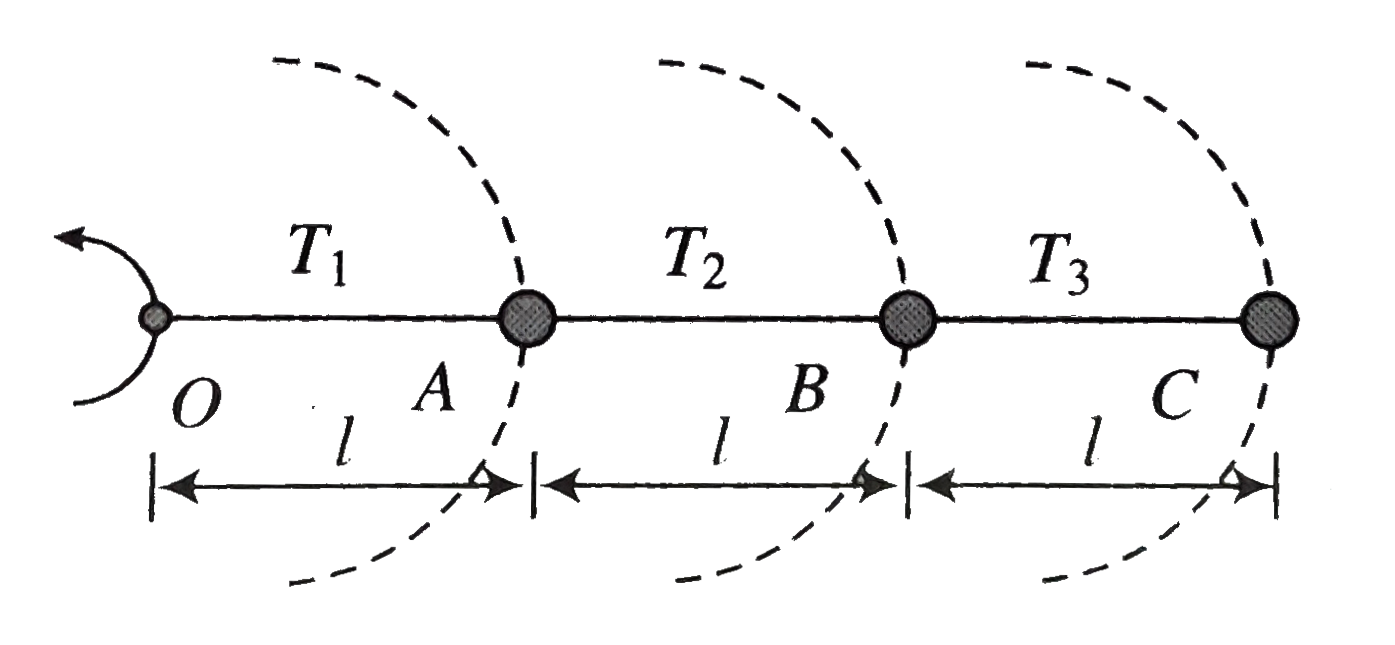
Three identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is v0 then the ratio of tension in the three sections of the string (T1:T2:T3=?) is
3:5:7
3:4:5
7:11:6
3:5:6
The correct Answer is:D
Let omega is the angular speed of revolution.
T3=mω23l
T2−T2=mω22l implies T2=mω25l
T1−T2=mω22l implies T1=mω26l
T3:T2:T1=3:5:6 . 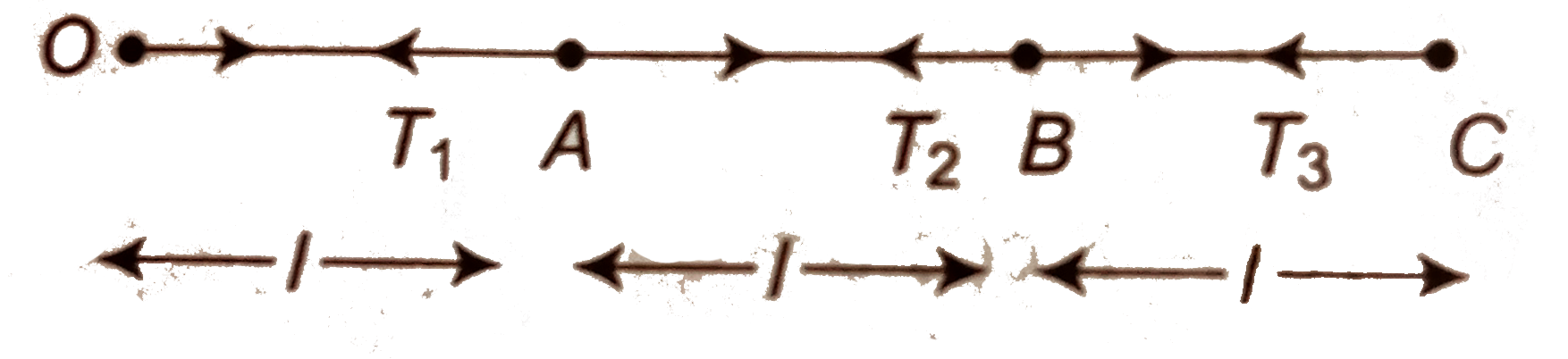
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Problems Based On Mixed Concepts
Explore 51 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Basic Concept Of Static And Kinetic Frictions
Explore 45 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
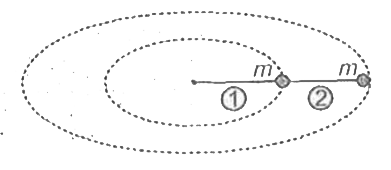
Two particles each of mass m are moving in horizontal circle with same angular speed. If both string are of same length then the ratio of tension in string T1T2 is
View SolutionAcceleration of two identical particles moving in a straight line are as shown in figure.
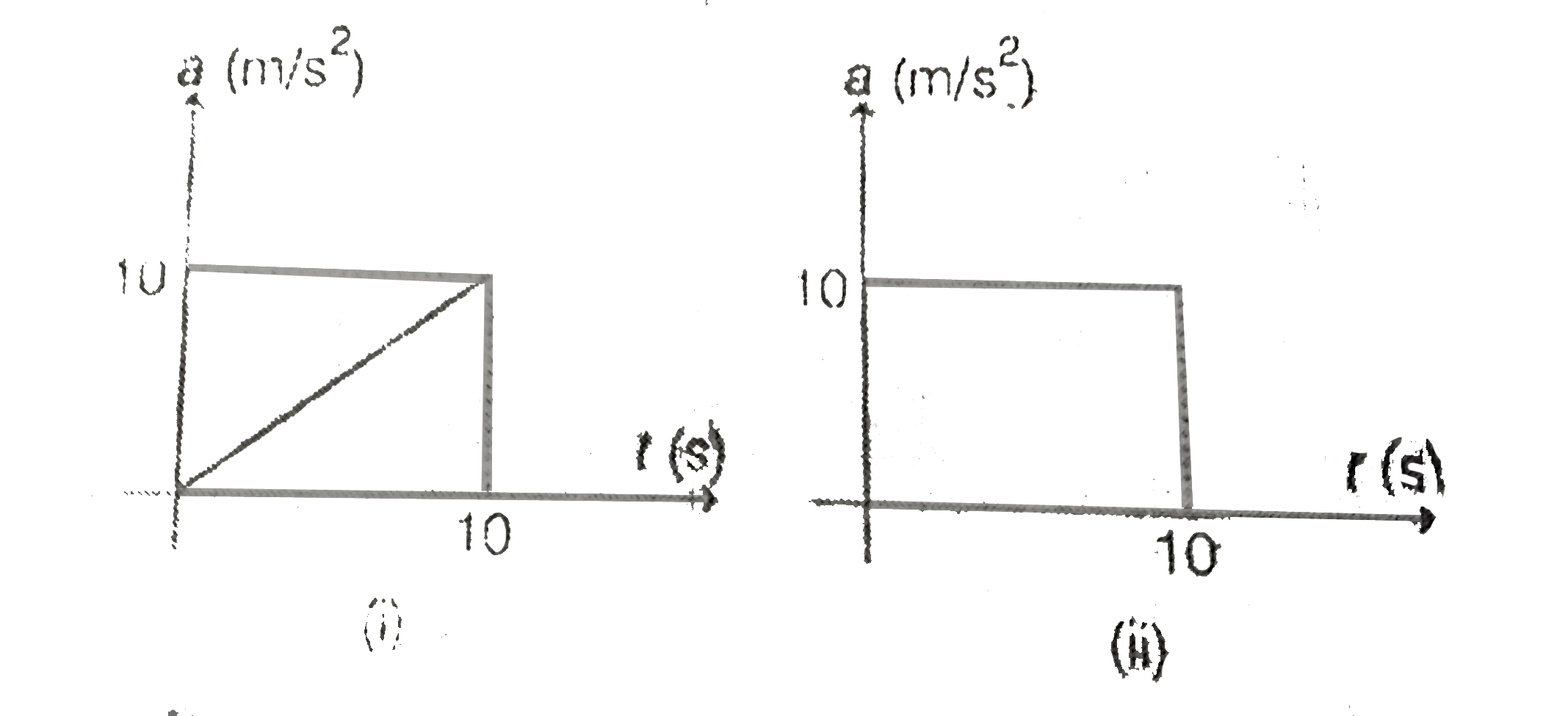
The corresponding a-t graph of their centre of mass will be
View Solution
Knowledge Check
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v0, then the ratio of tensions in the three sections of the string is (TBC:TAB:TDA)
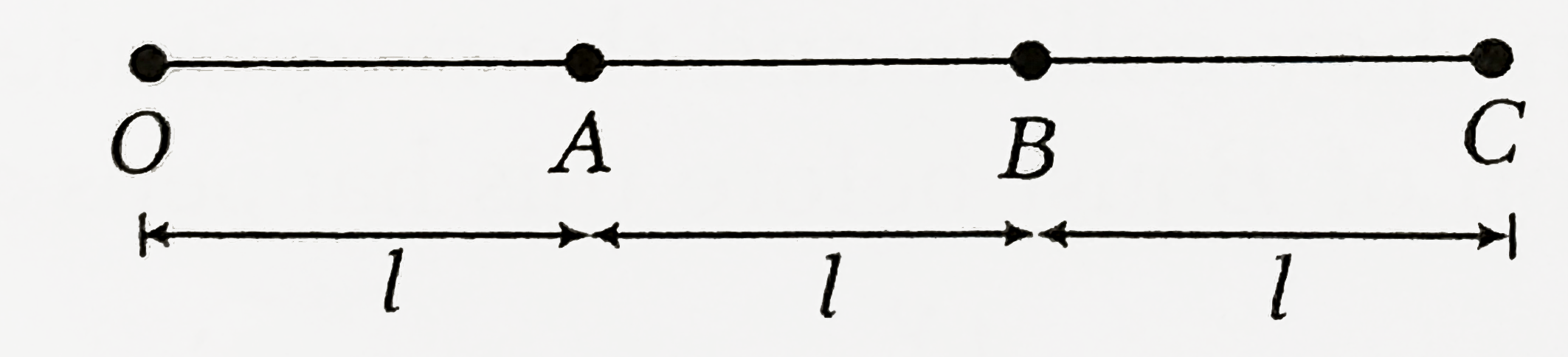 A3:5:7B3:4:5C7:11:6D3:5:6
A3:5:7B3:4:5C7:11:6D3:5:6A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlThe x-t graph of a particle moving along a straight line is shown in figure
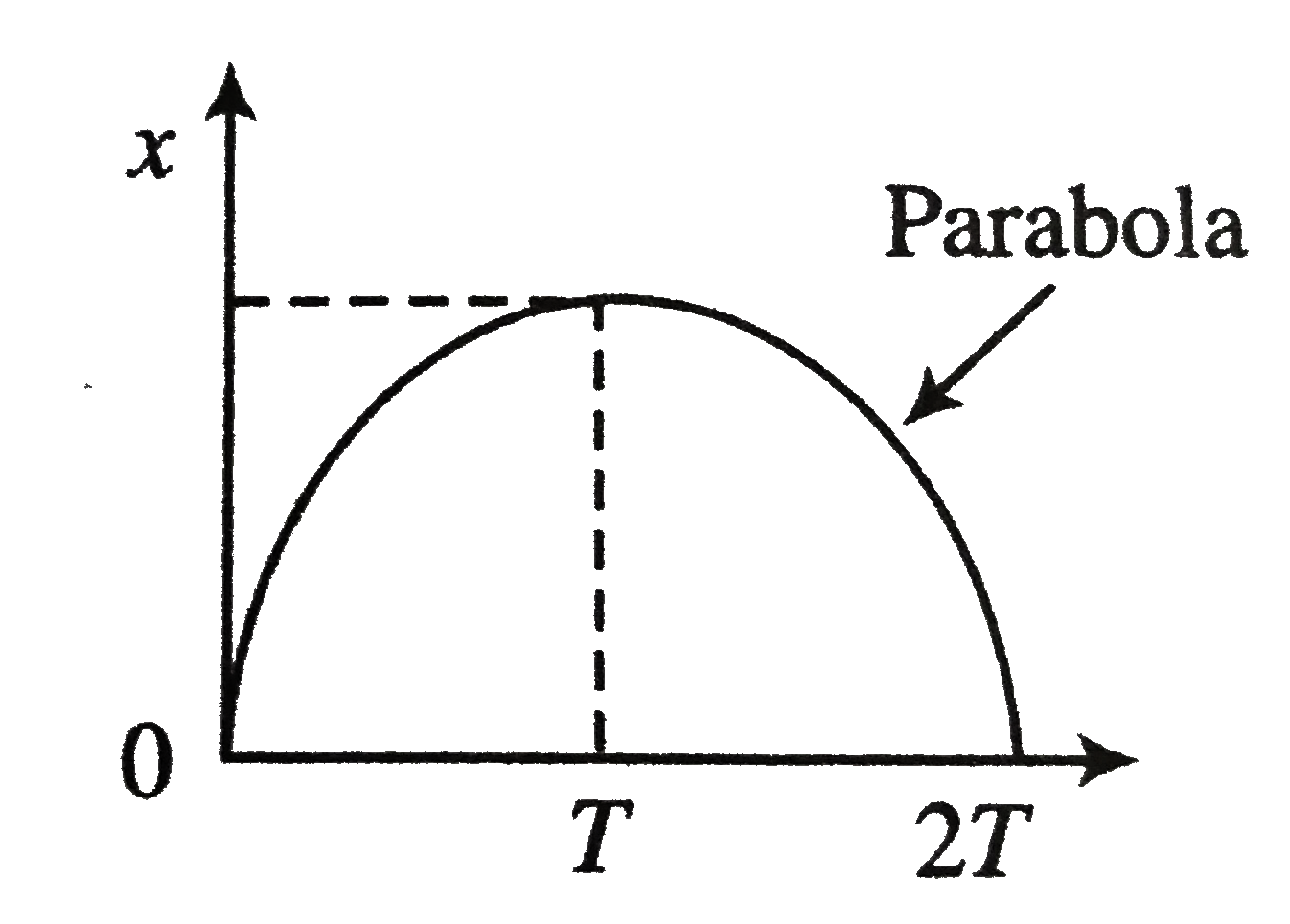
The v-t graph of the particle is correctly shown byA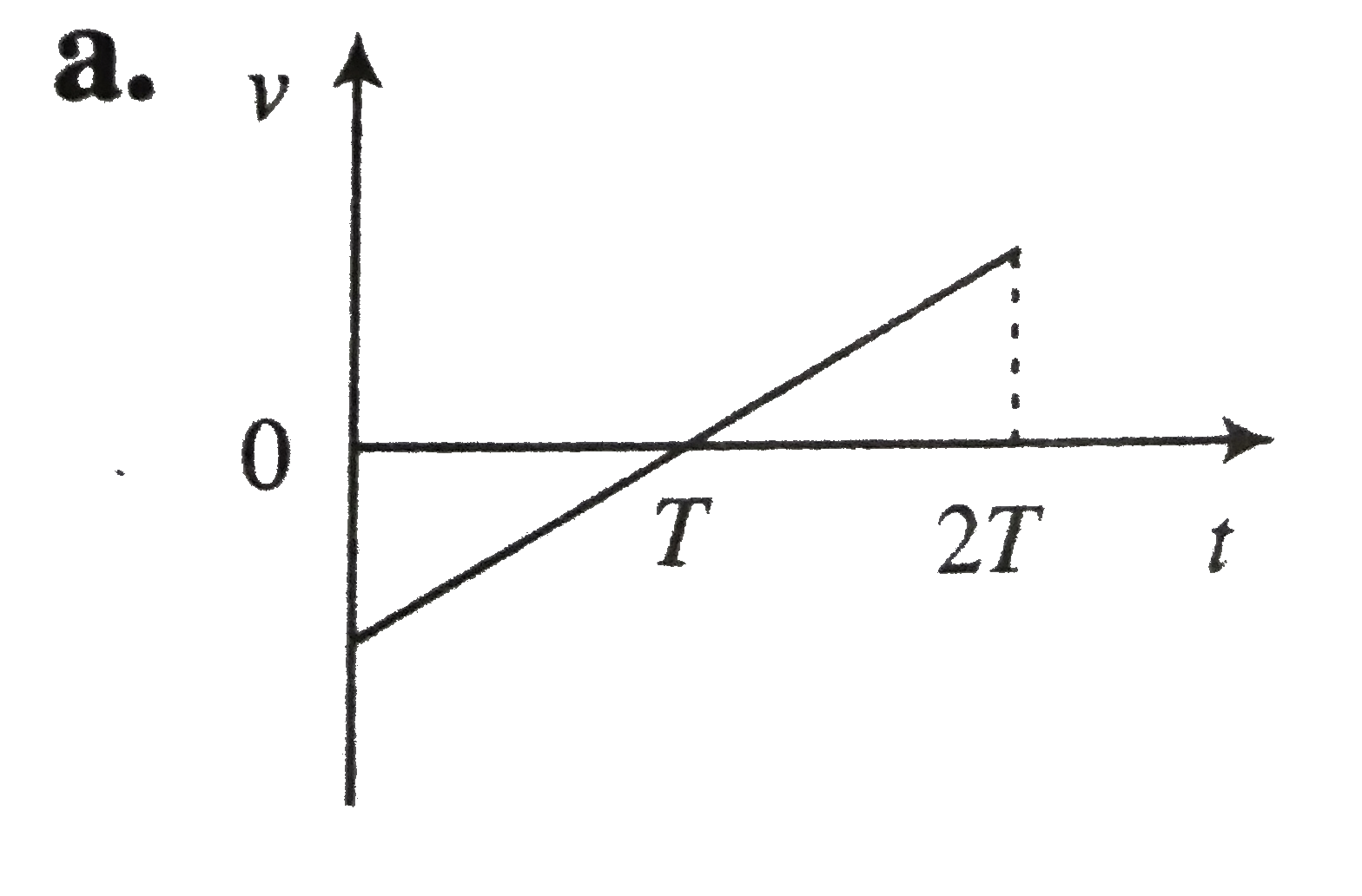 B
B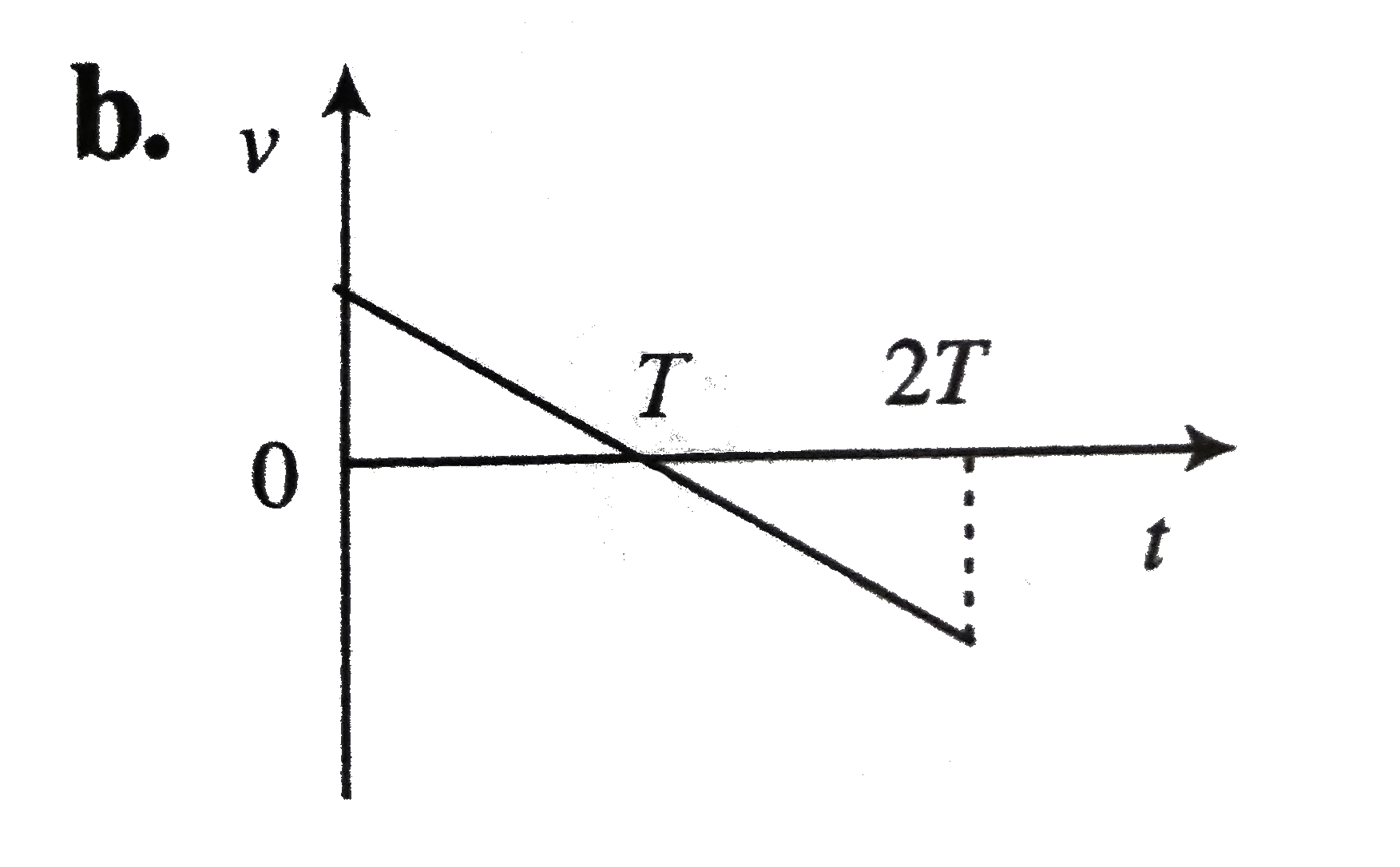 C
C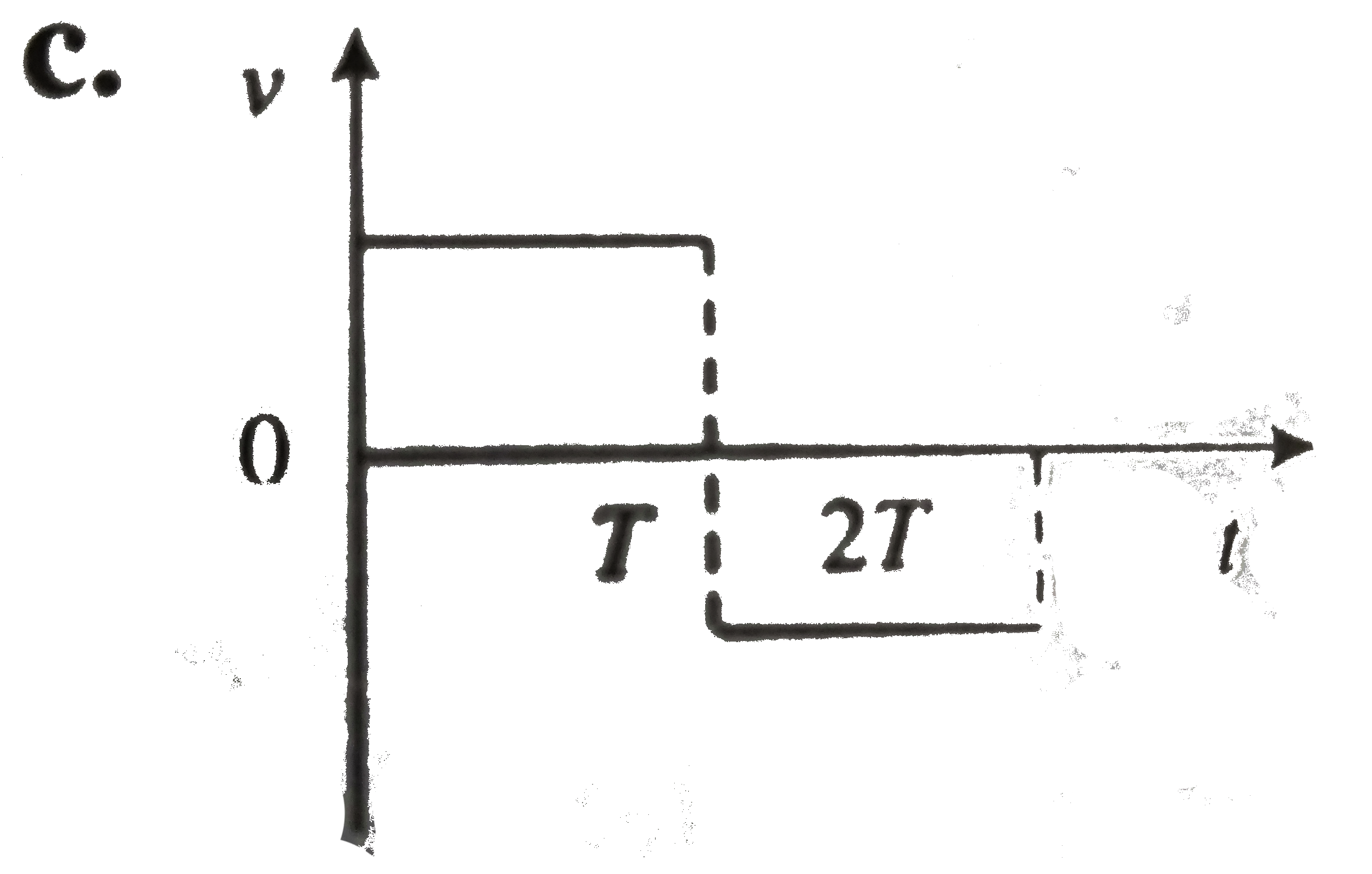 D
D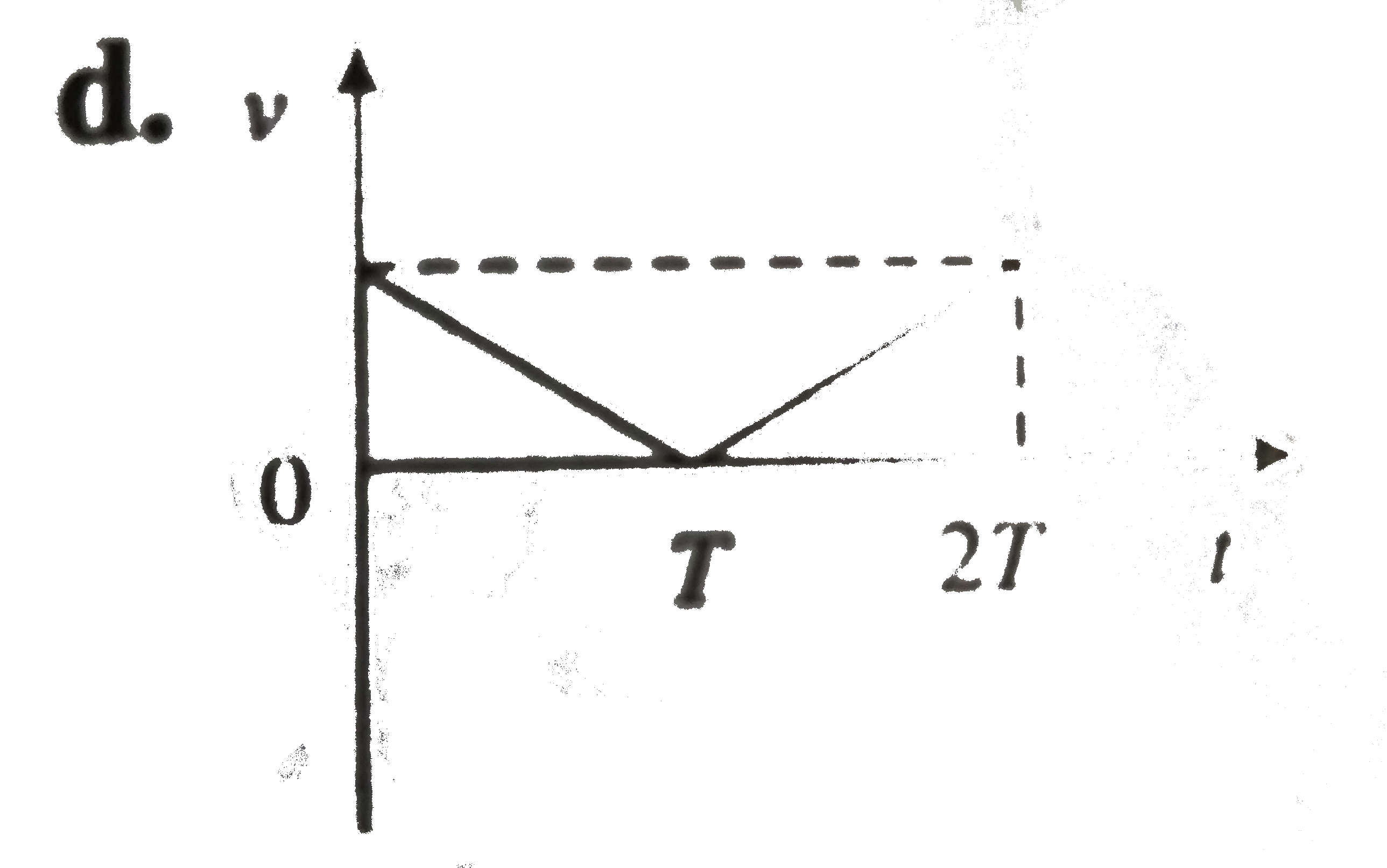
A rod AB of mass m is hung by two ideal threads. Find the ratio of tensions in the two threads (T1T2).
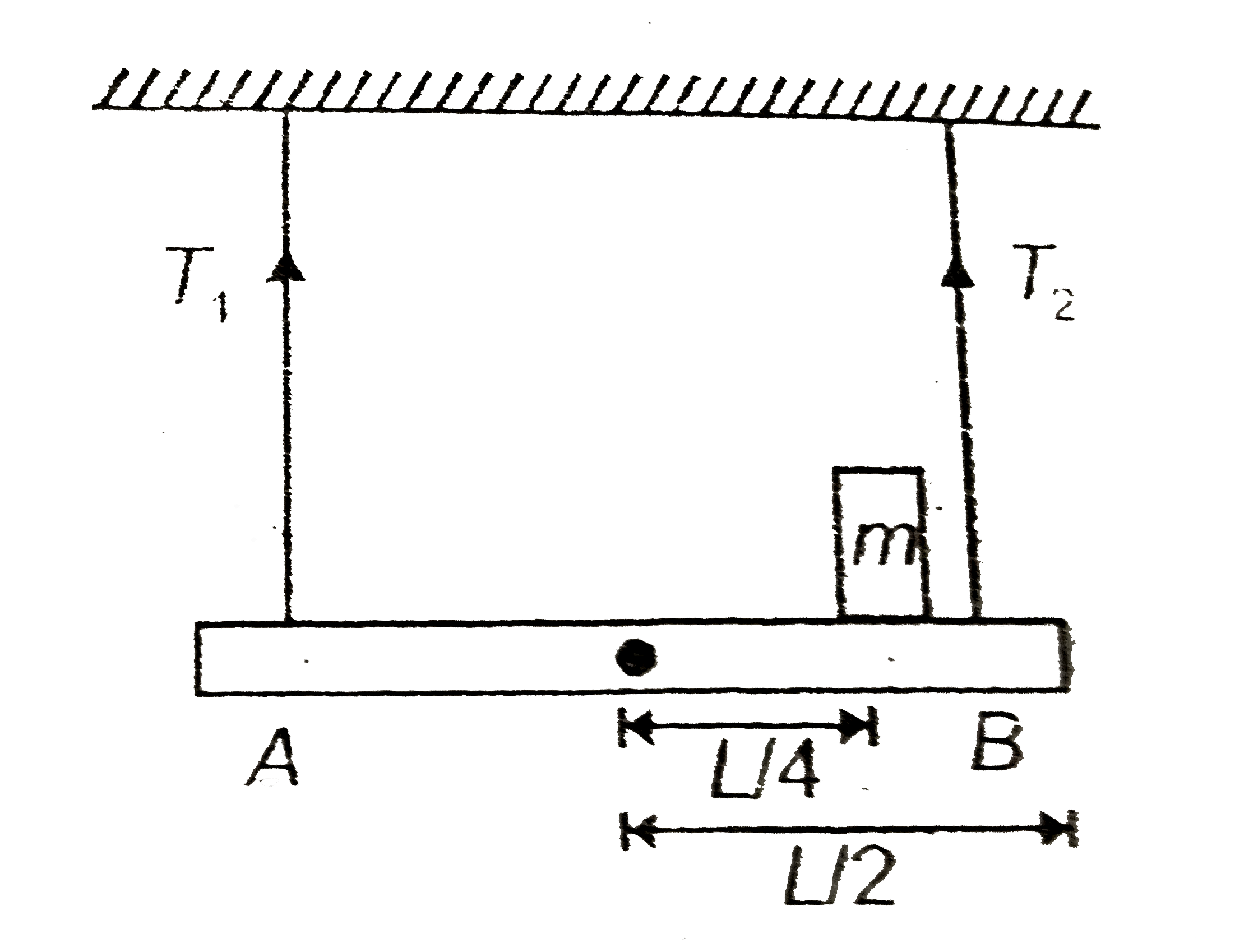
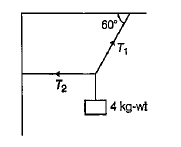
View SolutionDetermine the tensions T1 and T2 in the strings as shown in figure.
View SolutionThe x−t graph of particle moving along a straight line is shown in figure

The v−t graph of the particles is correctly shown by
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
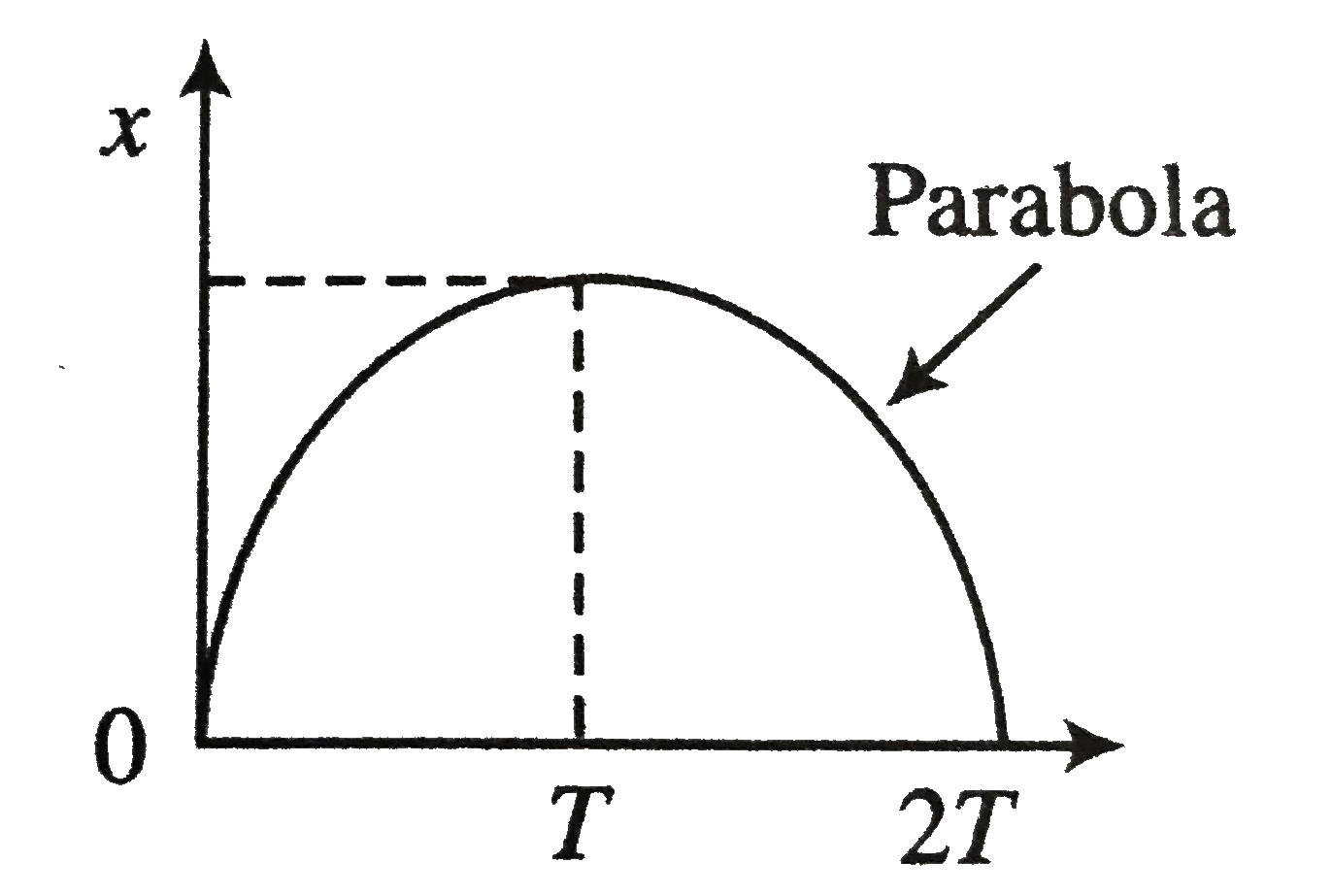
The a-t graph of the particle is correctly shown by
View SolutionThe x−t graph of particle moving along a straight line is shown in figure
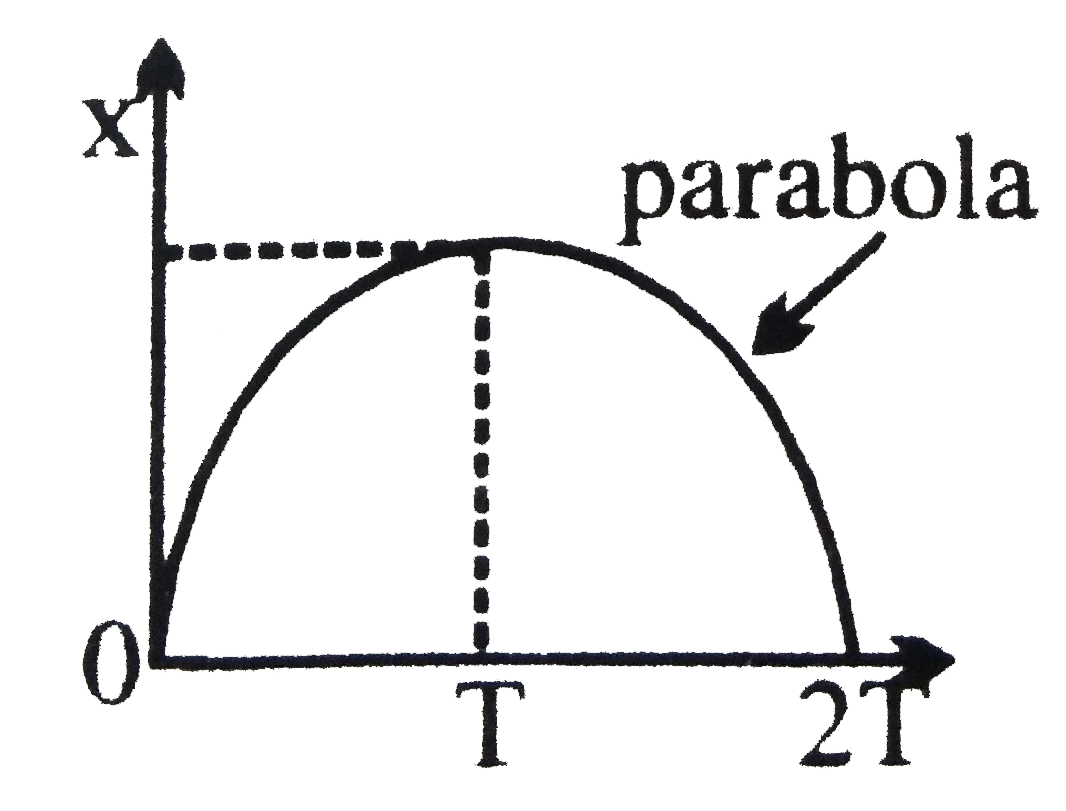
The a−t graph of the particle is correctly shown by
View Solution

