Two particles P and Q are located at distance rpandrQ respectively form the centre of rotating disc such that rP>rQ. The disc is rotating with constant angular acceleration. We can say
both P and Q have the same acceleration
both P and Q do not have the same acceleration
P has greater acceleration than Q
Q has greater acceleration than P
The correct Answer is:c
Resultant acceleration,
a=√a2r+a2t=√(ω2r)2+(rα)2
⇒a=r√(ω2)2+(α)2
As ωnandα will be same for both the particles P and Q, hence ap>aQ(∴RP>rQ)
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Problems Based On Mixed Concepts
Explore 35 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Assertion Reasoning
Explore 11 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Relative Velocity In Two Dimensions
Explore 23 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
Two particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
Aboth p and q have the same accelerationBboth p and q do not have any accelerationCp has greater acceleration then qDq has greater acceleration than pTwo particles P and Q are located at distance rpandrQ respectively form the centre of rotating disc such that rP>rQ. The disc is rotating with constant angular acceleration. We can say
ABoth P and Q have the same acceelerationBBoth P and Q do not have any accelcrationCP has greater acceleration than QDQ has greater acceleration than PTwo particles A and B are located at distances rA and rB from the centre of a rotating disc such that rA>rB . In this case
(Angular velocity (ω) of rotation is constant)Aboth A and B do not have any accelerationBboth A and B have same accelerationCA has greater acceleration than BDB has greater acceleration than B
Two loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View SolutionCharge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
View SolutionIf p,q and r are simple propositions such that (p∧q)∧(q∧r) is true, then
View SolutionIf p→q(q∨r) is false, then the truth values of p,q,r are respectively
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
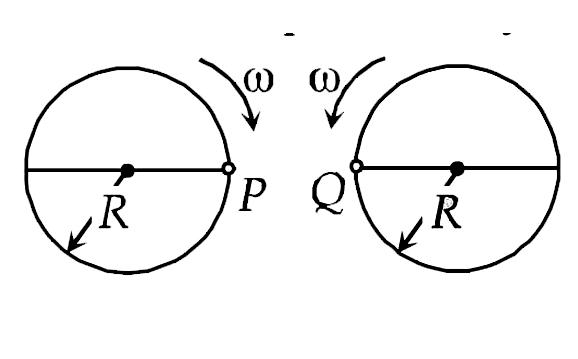
View Solution