ˆer is unit Vector along radius of a circle shown in figure ˆer can be represented as
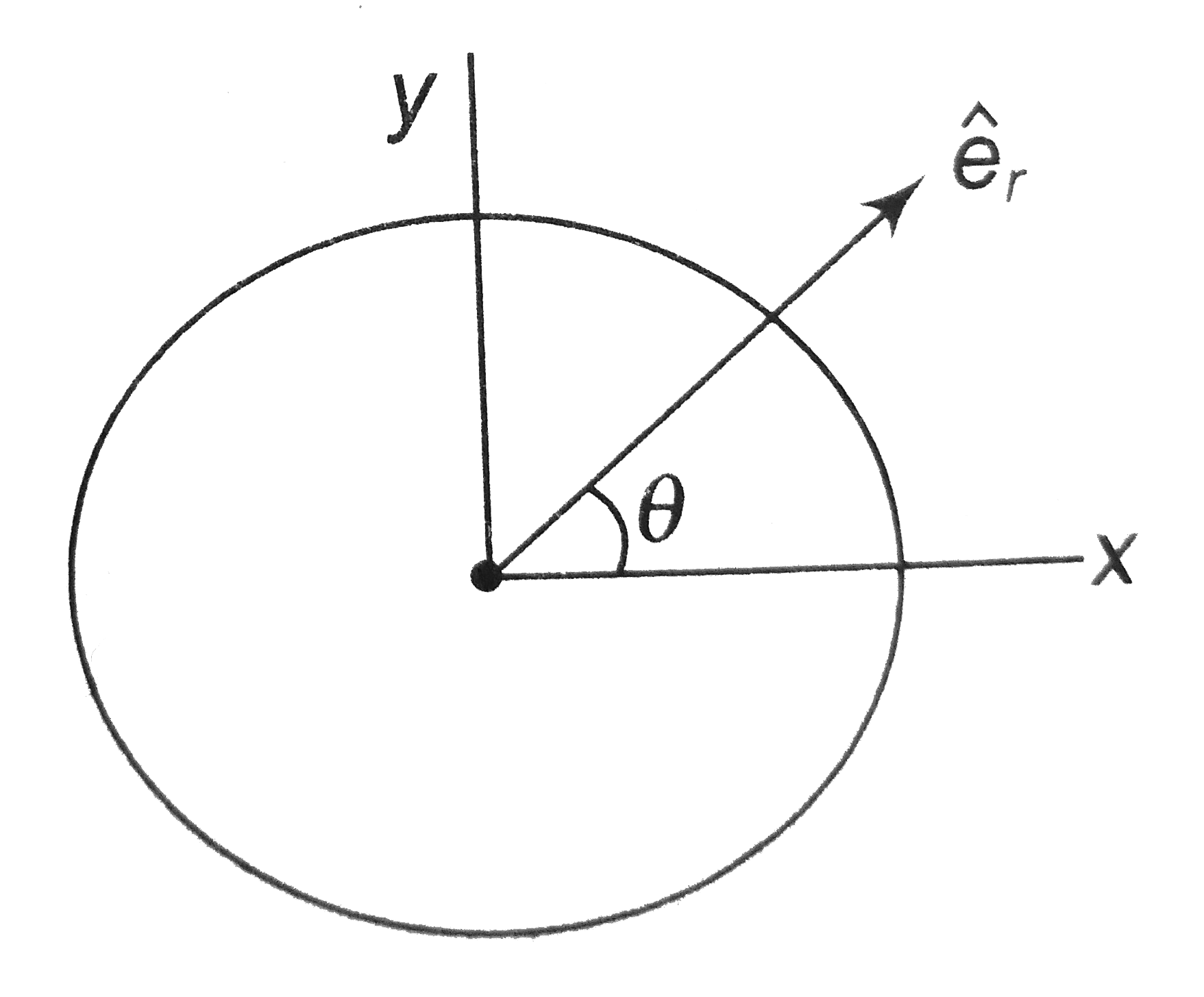
cosθˆi+sinθˆj
sinθˆi+cosθˆj
cosθˆi−sinθˆj
−cosθˆi+sinθˆi
The correct Answer is:A
The component of ˆer along X-axis is
ˆercosθ=1×cosθ=cosθ
The component of ˆer along Y-axis is
ˆersinθ=1×sinθ=sinθ
∴ˆer=cosθˆi+sinθˆj
Topper's Solved these Questions
Similar Questions
A spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
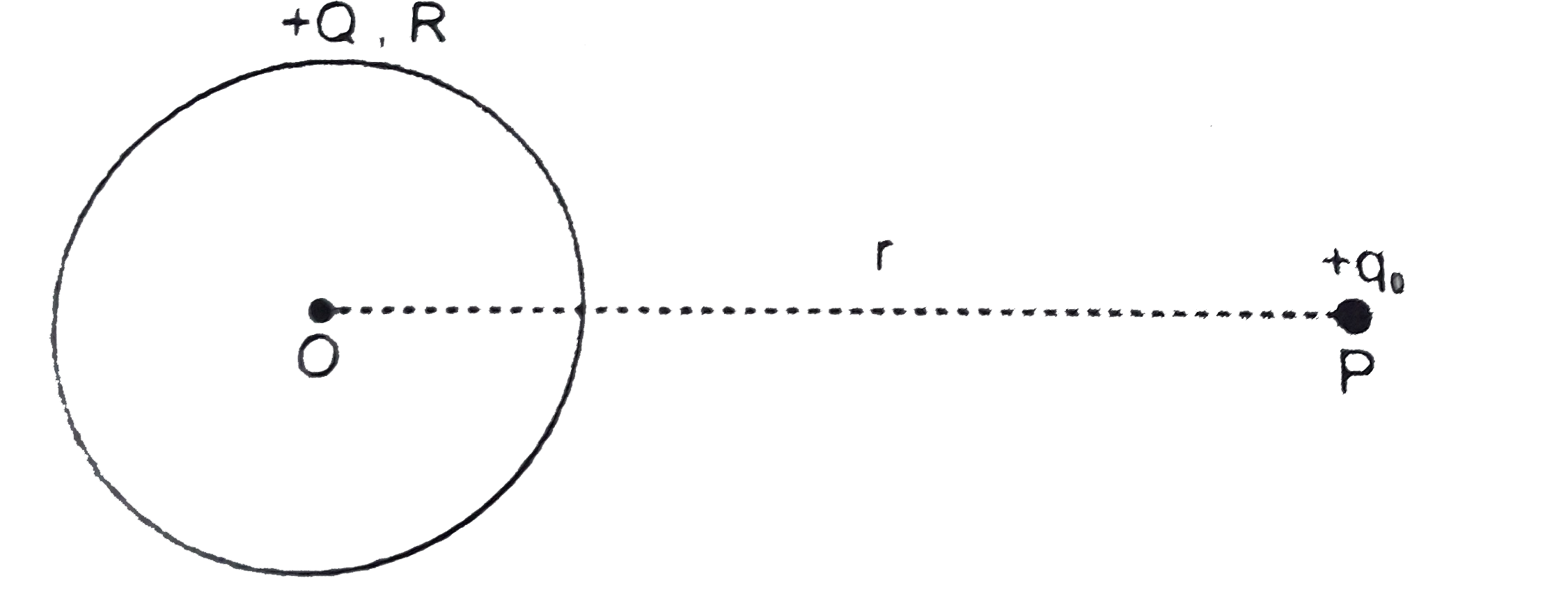
(i) Force on the point charge +q0 due to the shell =q→E0 shell=(q0)(KQr2)ˆr=KQq0r2ˆr where ˆr. is unit vector along OP.
From action - reaction principle, force on the shell due to the point charge will also be : Fshell=KQq0r2(−ˆr)
Conslusion : To find the force on a hollow sphere due to outside charges, we can replace the sphere by a point charge kept at centre.
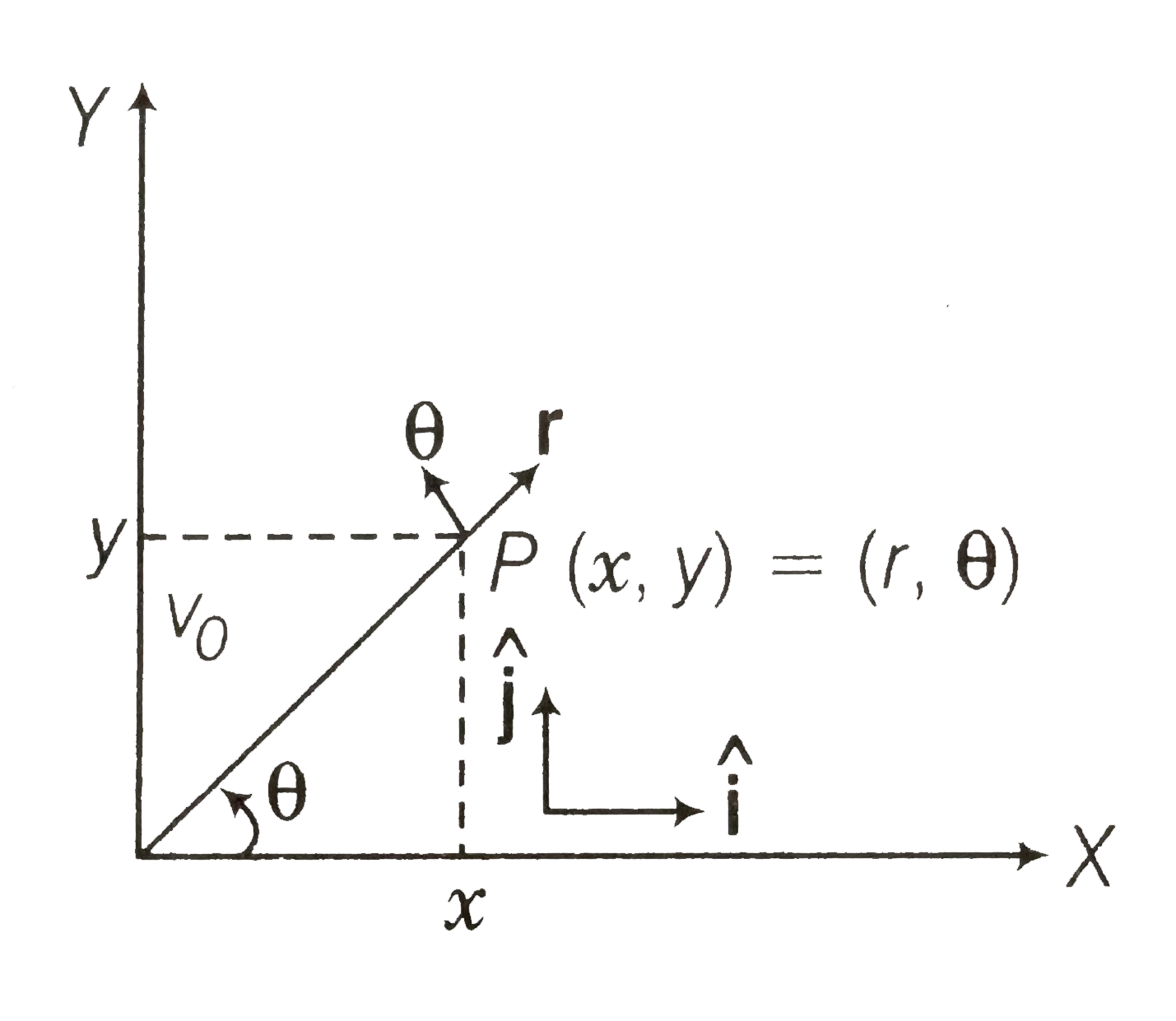
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=Axˆi+Ayˆj, where ˆi and ˆj are unit vector along x and y-directions, respectively and Ax and Ay are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A=Arˆr+Aθˆθ, where ˆr=rr=cosθˆi+sinθˆj and ˆθ=−sinθˆi+cosθˆj are unit vectors along direction in which r and θ are increasing.
(a) Express ˆi and ˆj in terms of ˆr and ˆθ.
(b) Show that both ˆr and ˆθ are unit vectors and are perpendicular to each other.
(c) Show that ddt(ˆr)=ωˆθ, where ω=dθdt and ddt(ˆθ)=−θˆr.
(d) For a particle moving along a spiral given by r=aθˆr, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View Solution
Knowledge Check
The unit vector along ˆi+ˆj is
AˆkBˆi+ˆjCˆi+ˆj√2Dˆi+ˆj2Unit vector along 3ˆi+3ˆj is
Aˆi+ˆj√2B3ˆi+3ˆj2Cˆi+ˆjDˆi+ˆj√3If ˆi denotes a unit vector along incident light ray, ˆr a unit vector along refracted ray into a medium of refractive index μ and ˆn unit vector normal to boundary of medium directed towards incident medium, then law of refraction is
Aˆi.ˆn=μ(ˆrˆn)Bˆi׈n=μ(ˆn׈r)Cˆi׈n=μ(ˆr׈n)Dμ(ˆi׈n)=ˆr׈n
(a) Derive an expression for unit vector along reflected ray (ˆr) if unit vectors ˆi and ˆn represents unit vectors along incident light ray and normal (at point of reflection and outward from surface) respectively.
(b) If vector along the incident ray on a mirror is −2ˆi+3ˆj+4ˆk. Considering the x-axis to be along the normal. Then, find the unit vector along the reflected ray.
View SolutionIf ˆi denotes a unit vector along incident light ray, ˆra unit vector along refracted ray into a medium of refraction index μ and ˆn unit vector normal to boundary of medium directed towards incident medium, then law of refraction is
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionA unit vector along the direction ˆi+ˆj+ˆk has a magnitude :
View SolutionPosition vector →A is 2ˆi
Position vector −→B0 is 3ˆj
ˆi,ˆj,ˆk are along the shown x,y, and z is
−4→A can be represented as
View Solution

