The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
3
4
5
8
The correct Answer is:B
To find the magnitude of the y-component of vector →A, we can use the Pythagorean theorem. The relationship between the components of a vector and its magnitude is given by:
|→A|=√(Ax)2+(Ay)2
Where:
- |→A| is the magnitude of the vector,
- Ax is the x-component of the vector,
- Ay is the y-component of the vector.
1. Identify Given Values:
- The magnitude of vector →A is given as 5.
- The x-component Ax is given as 3.
2. Set Up the Equation:
Using the Pythagorean theorem, we can set up the equation:
5=√(3)2+(Ay)2
3. Square Both Sides:
To eliminate the square root, we square both sides of the equation:
52=(3)2+(Ay)2
This simplifies to:
25=9+(Ay)2
4. Isolate A2y:
Rearranging the equation to isolate (Ay)2:
(Ay)2=25−9
(Ay)2=16
5. Take the Square Root:
Now, take the square root of both sides to find Ay:
Ay=√16
Ay=4
6. Conclusion:
The magnitude of the y-component of vector →A is 4.
Final Answer:
The magnitude of the y-component of vector →A is 4.
- |→A| is the magnitude of the vector,
- Ax is the x-component of the vector,
- Ay is the y-component of the vector.
- The magnitude of vector →A is given as 5.
- The x-component Ax is given as 3.
Using the Pythagorean theorem, we can set up the equation:
5=√(3)2+(Ay)2
To eliminate the square root, we square both sides of the equation:
52=(3)2+(Ay)2
This simplifies to:
25=9+(Ay)2
Rearranging the equation to isolate (Ay)2:
(Ay)2=25−9
(Ay)2=16
Now, take the square root of both sides to find Ay:
Ay=√16
Ay=4
The magnitude of the y-component of vector →A is 4.
The magnitude of the y-component of vector →A is 4.
Topper's Solved these Questions
- VECTORSBook:A2ZChapter:VECTORSExercise:Resultant Of Vectors
Explore 24 Videos
- VECTORSBook:A2ZChapter:VECTORSExercise:Expressing Vectors In Unit Vector Notation
Explore 22 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBook:A2ZChapter:UNIT, DIMENSION AND ERROR ANALYSISExercise:Chapter Test
Explore 28 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
The sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
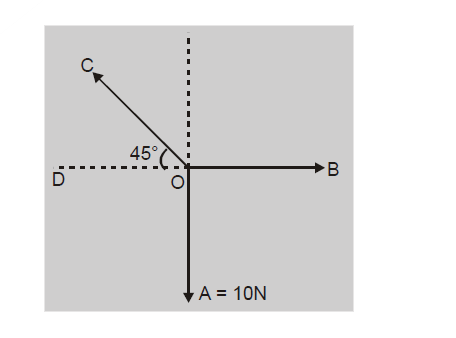
(ii) What is the magnitude of vector −−→OC ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
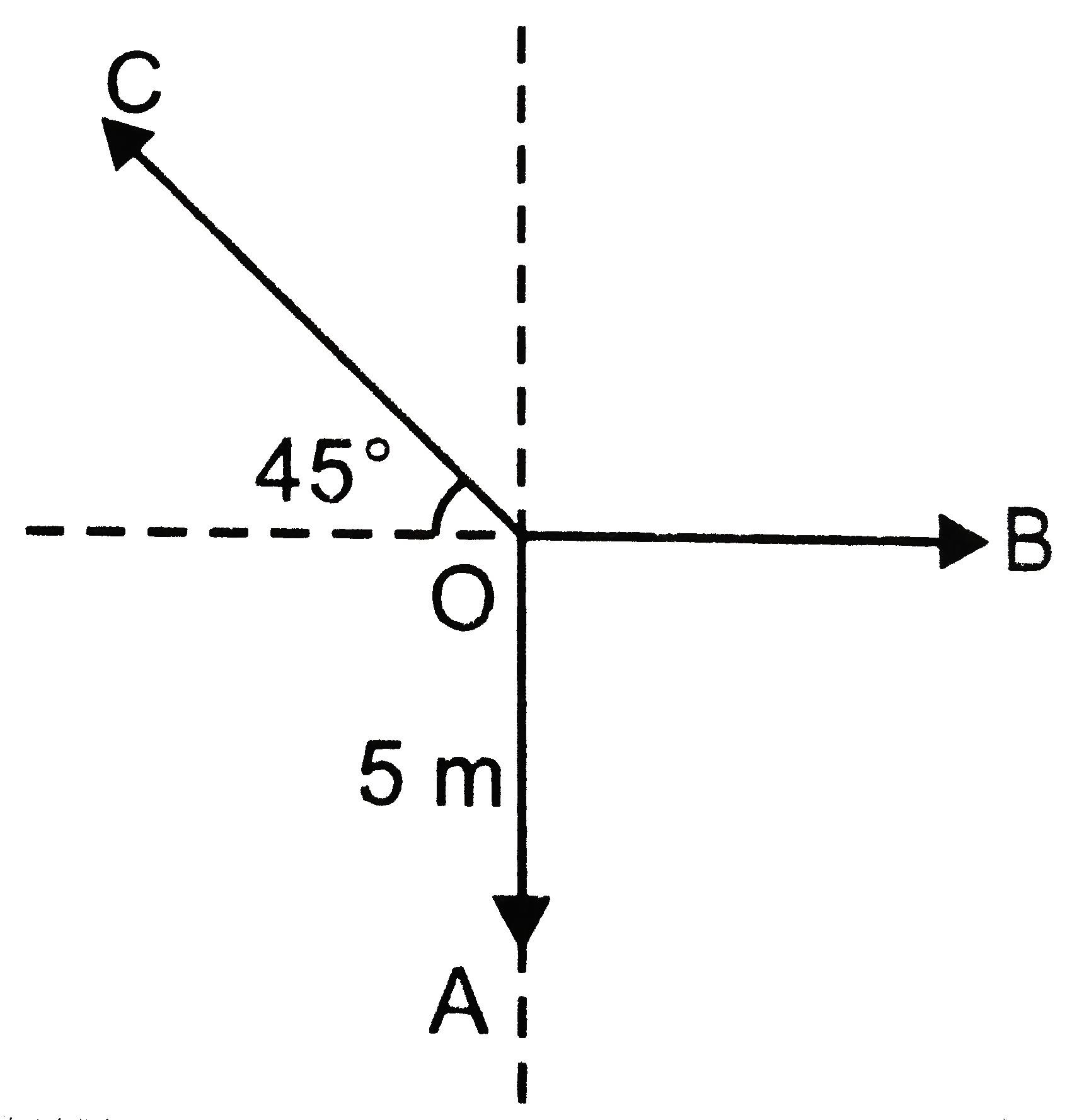 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View Solution
Knowledge Check
If →A is a vector of magnitude 3 units due east. What is the magnitude and direction of a vector −4→A ?
A3 units due eastB4 units due eastC12 units due eastD12 units due westIf →A is a vector of magnitudes 5units due east. What is the magnitude and direction of a vector −5→A?
A5 units due eastB25 units due westC5 units due westD25 units due east→A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 →A ?
A4 units due eastB4 units due westC2.7 units due eastD10.8 units due east
The x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
View SolutionThe x−component of a certain vertor is 2 units and y−component is +2√3 units. What is the magnitude of vector.
View SolutionWrite the magnitude of the vector →a in terms of dot product.
View SolutionThe magnitude of x and y components of →A are 7 and 6 respectively . Also , the magnitudes of x and y components of →A+→B are 11 and 9 respectively . Calculate the magnitude of vector →B
View SolutionThe resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
View Solution

