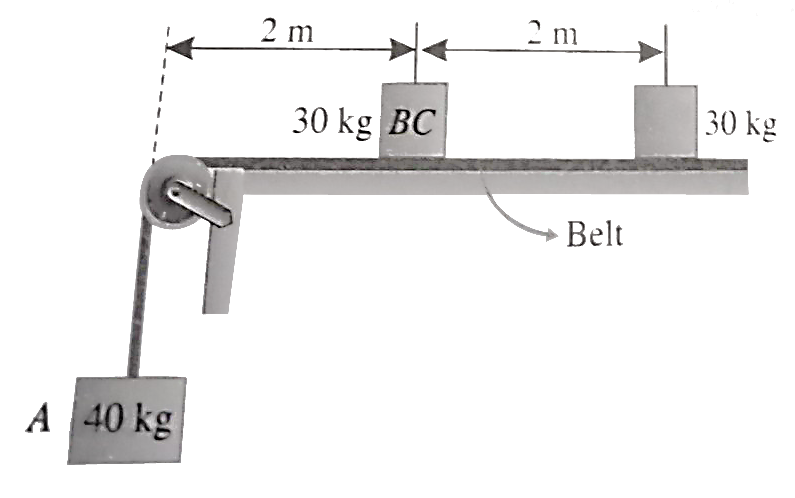
Two 30 kg blocks rest on a massless belt which passes over a fixed pulley and is attached to a 40 kg block. If coefficient of friction between the belt and the table as well as between the belt and the blocks B and C is μ and the system is released from rest from the position shown, the speed with which the block B falls off the belt is
2√2ms if μ=0.2
√2ms if μ=0.2
2ms if μ=0.5
2.5ms if μ=0.5
The correct Answer is:A, C

Maximum possible acceleration of block will be =μg
(i) When μ=0.2 maximum acceleration possible so that blocks does not slip is 2ms2. Now acceleration of system assuming blocks don't slip is
As 3.8>2 hence the assumption is wrong and blocks slip on the belt.
Maximum force applicable on block B is μmg
Acceleration of block=2ms2
Hence velocity of B when it strikes pulley is V2=02+2×2×2
V2=8
V=2√2ms
Hence (a).
(ii) When μ=0.5 maximum acceleration possible so the block dows not slip is 5ms2
Now acceleration of system assuming blocks don't slip is
a=40g−2μmg100=1ms2
μ=0.5
as 1<5 hence, blocks do not slip and acceleration of block B is 1ms2
hence velocity of B when it strikes pulley is
V2=02+2.1.2
V2=4
V=2ms
Hence (c).
Similar Questions
Two blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
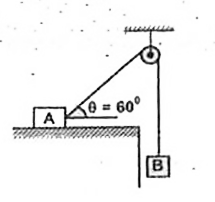
View SolutionConsider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)

View Solution
Knowledge Check
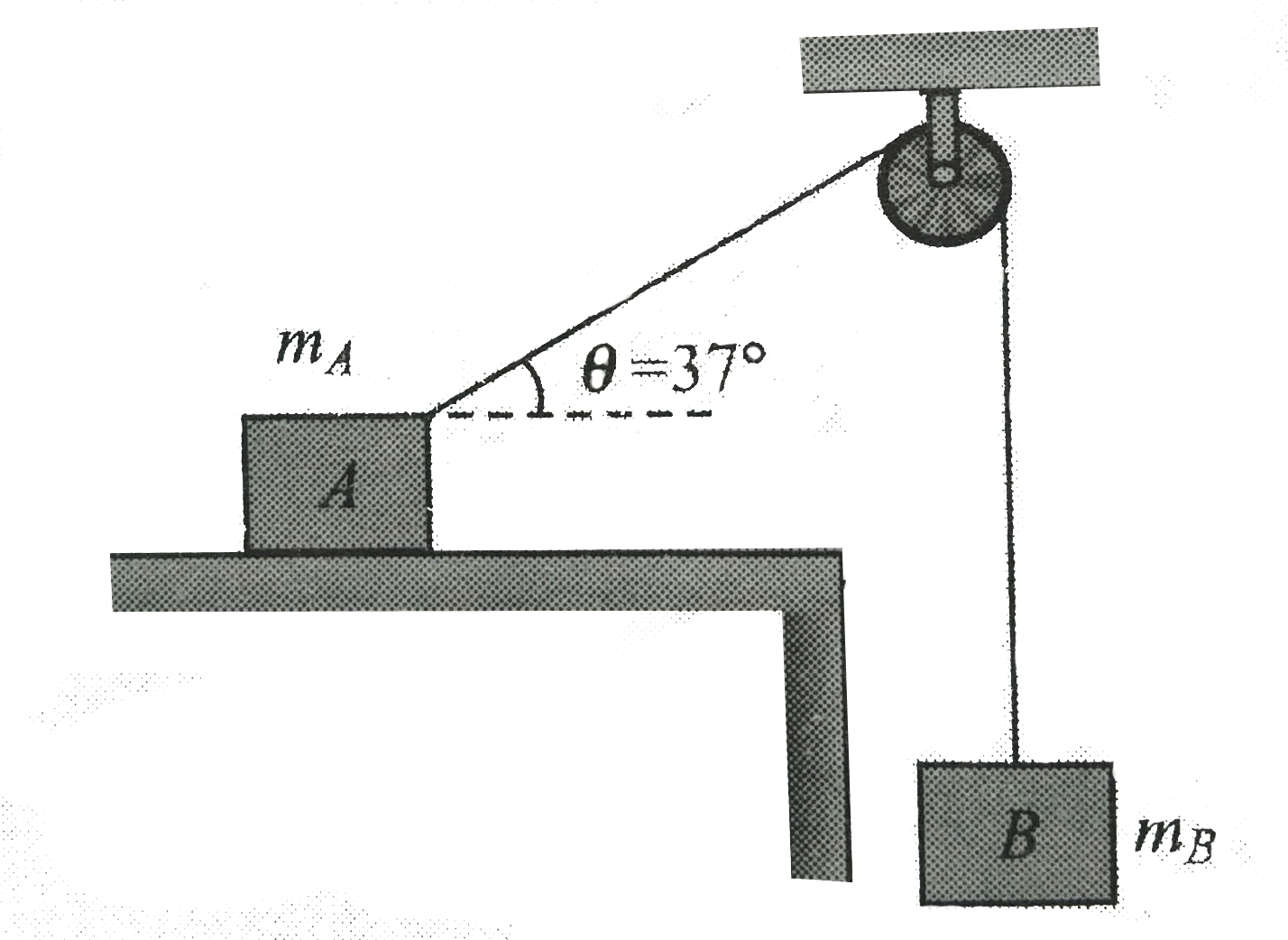
The coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between A&B is released from rest & there is no slipping between A&B then:
 A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)Two blocks A and B are connected by a light inextensible string passing over a fixed smooth pulley as shown in figure The coefficient of friction between the block A and B the horizontal table is μ=0.5. If the block A is just , find ratio of the masses of the blocks
 A125B115C135D175
A125B115C135D175The coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
 A2θ<sin−1(2μ)Bθ<tan−1(μ)C2θ<cos−1(2μ)D2θ<tan−1(μ/2)
A2θ<sin−1(2μ)Bθ<tan−1(μ)C2θ<cos−1(2μ)D2θ<tan−1(μ/2)
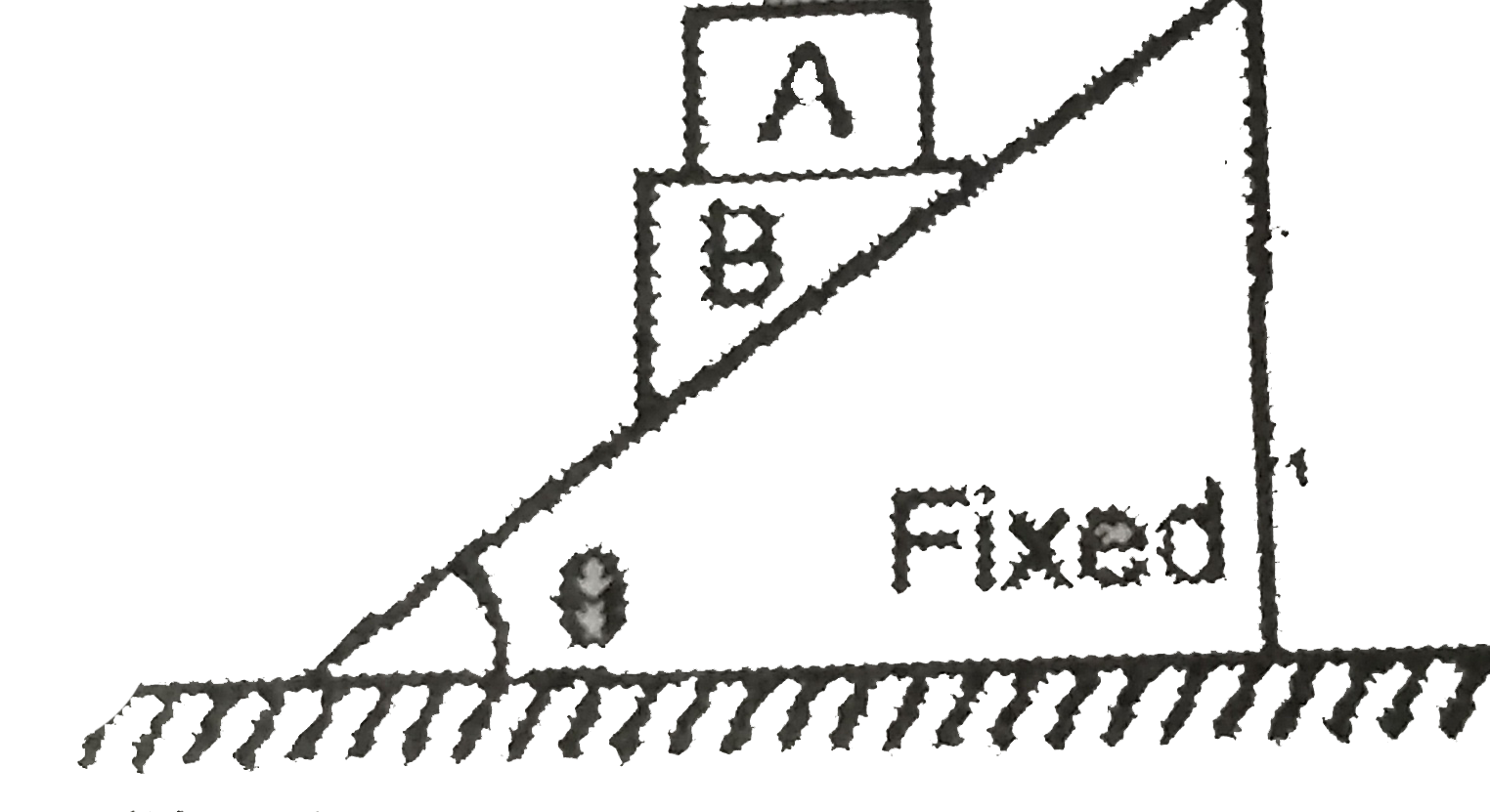
consider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)
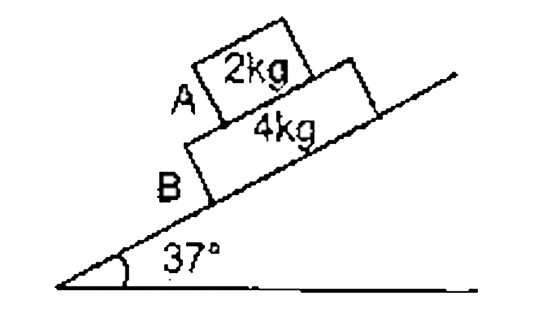
In the previous question the frictional force between block B and plane is :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)

The frictional force acting between the two blocks in the previous question is :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)

The frictional force acting between the blocks in the previous case :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)

The frictional force acting between the blocks in the previous case will be:
View SolutionConsider the situation shown in figure in which a book 'A' of mass 2kg is placed over a block 'B' of mass 4kg. The combination of the placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between blocks B and inclined plane is μ2 and in between the two bolcks is μ1, The system is released from rest.
( Take g=10m/sec2)

In the previous question the frictional force between block B and plane is:
View Solution

